AI and Graph Search
Let's explore artificial intelligence, old school algorithms, breadth-first search, and more.
Join the DZone community and get the full member experience.
Join For Free
Pretty often, when I look at some AI-related topics, tutorials, or articles, I see that the graph search problem is presented as an example of how AI agents work. So, why is that? What is the relation between some classic graph searching problems and AI?
What Is Artificial Intelligence?
Looking around, you will see that there isn’t a clear and single definition of artificial intelligence. Some say that “Artificial intelligence is defined as a study of rational agents” where "a rational agent could be anything that makes decisions like a person, firm, machine, or software. It carries out an action with the best outcome after considering past and current percepts (agent’s perceptual inputs at a given instance)". Other definitions are more philosophically trying to find the border between human natural intelligence and what a machine can do.
But all the definitions are trying to say that AI is actually the discipline when you want to know what to do when you don’t know what to do. And here comes a rational agent, that, by perceiving the environment by some sensors and looking at the old actions that it already executed, it tries to choose the next action with the best possible outcome.8
So let’s look at a classic route-finding problem. We have a graph with many nodes and you try to find the path with the minimum cost between two nodes. And here comes the definition of an AI agent. You don’t exactly know what’s the path, and a rational agent, by perceiving the environment, in our case the graph, will find that path.
But we know that there are many algorithms that are able to solve the graph search problem. Just look at the DFS, BFS, Dijkstra, or A*. Some of us know this algorithm from high school. So what’s new here? Is that actually what an AI agent does? Well yes, but not only this. AI is not just a programming paradigm, like the graph search algorithms, but, as I said before, it's a study of rational agents that study the environment and try to choose the action with the best outcome.
An AI agent is a broad term. They go as far as machine learning, neural networks, deep learning, and much more, and they are used in finance, medical institutions, security, etc. So the graph search is just a small subtype of AI.
The difference between a classic graph search algorithm and an AI agent that is able to find the shortest path between two nodes is just a difference of terminology. And it is important to understand this aspect as if you try to create an AI agent that is not actually a different thing than an old school algorithm.
Old School Algorithms
There are many ways to implement a graph search. There are the classic algorithms like BFS and DFS that are able to find the goal node without calculating the optimal path, and there are algorithms like Unifrom Cost search, Dijkstra, or A* that are able to calculate the shortest path from a source to a goal. All these algorithms are tree-based algorithms, where the only catch is that graphs, unlike trees, may contain cycles.
The main point of all these algorithms is that after we visit a node, we have to pick the next unvisited node and “visit” it in order to see if we reached the goal or not.
More About BFS
Like I said before, breadth-first search is a tree-based algorithm. Its name comes from the idea that the graph traversal is layer-wise. Starting from the source node, we first explore the neighbors and then we move further down.
Let’s look at the picture below:

Starting from node A, we see how this graph can turn into a tree.
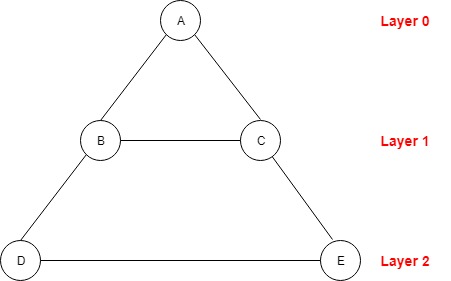
A is the starting node staying on Layer 0, then B and C are on Layer 1, and then D and E are on Layer 2. This is the order in which BFS will traverse this graph.
If we traverse this graph using BFS, the order will be: A -> B -> C -> D -> E.
Looking carefully at the tree and we will see that there are some connections between B and C and E and D. This happens because our graph contains cycles. But if we want to traverse it optimally, we should not visit the already visited nodes again. So, one of the conditions when picking a node to visit is to be unvisited.
How the Algorithm Works
Considering that, after we visit the start node, we will continue to visit all of its neighbors and then we will proceed to the next “layer” and will need a queue. When we visit a node, we check its neighbors, and if the neighbors are not visited already, we add them to the queue. Then, we practically just pick the next node to visit from the queue. Another thing that we need to do is mark the visited nodes for not visiting them again. This way, we will visit all of the graph nodes only once.
Let’s look at the pseudocode:
BFS(G, s, goal)
Let Q be queue
Q.enqueue(s)
Mark s as visited
while (Q is not empty)
//Removing that vertex from queue
v = Q.dequeue()
If v is goal
return “found the goal”
//processing all the neighbours of v
for all neighbours w of v in Graph G
if w is not visited
//Stores w in Q to further visit its neighbour
Q.enqueue(w)
mark w as visitedSo, using this algorithm, we are able to find any node if there is at least a path between the start node and the goal.
Finding the Path With the Lowest Cost
Let’s change our graph by adding some costs on the vertices.
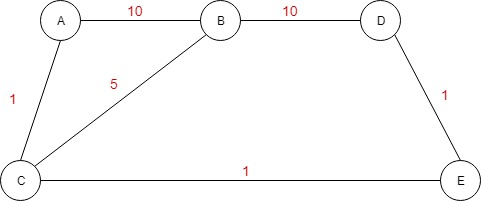
Now we want to go from A to D on the path with the lowest cost. We see that there are multiple ways to go from A to D. We could go on this path, A - > B -> D with the cost of 20, or we can choose A -> C -> B -> D with a lower cost of 16. But there is another path with the lowest cost of 3, A -> C -> E -> D. So, what should we do to find that path? We need to change the way of getting the next node to visit. In the classic BFS algorithm, we choose the next node to visit by using the FIFO queue order (first in, frist out). We would find the goal eventually but not the cheapest path. For getting to the goal on the path with the lowest cost, we need to make a change in the way of getting the next node to visit from the queue.
The algorithm that I am going to present to you is called the Uniform cost search, which is a slightly modified version of Dijkstra, where we stop when we find the destination. The classic Dijkstra algorithm continues to visit all nodes until the queue is empty, finding the minimum cost from the start node to every other node in the graph. What’s different from the BFS is that here, we have to store a new value representing the total cost so far from the start to the current visited node.
The queue will not be ordered by the FIFO rule, instead, we will order the queue based on the current cost so far value, prioritizing the unvisited nodes that have the lowest cost so far.
Let’s have a look at the code:
UniformCostSrearch(G, s)
s.costSoFar = 0;
for all nodes w in G except s
w.costSoFar = Int.maxInt
Let Q be a priority queue ordered by cost_so_far
Q.enqueue(s)
while (Q is not empty)
//Removing that vertex from queue
v = Q.dequeue()
If v is goal
return “found the goal”
//processing all the neighbours of v
for all neighbours w of v in Graph G
currentCost = dist[v,w]
newCost = v.costSoFar + currentCost;
If (newCost < w.costSoFar)
w.costSoFar = newCost ;
Q.enqueue(w)This way, we will choose the next node to visit based on the minimum cost so far for each node.
But the minimum cost so far needs to be updated because by exploring the graph, we can always find better ways to reach a node. For doing that, when we visit a node, we have a look at all its neighbors and we compare their current cost so far with a new cost, which is the sum between the visited node’s cost so far and the distance between this node and its neighbor:
currentCost = dist[v,w]
newCost = v.costSoFar + currentCost;
If (newCost < w.costSoFar) {
w.costSoFar = newCost ;
Q.enqueue(w);
}If the new cost is lower, this means that we found a better way to reach that node and we update that cost so far. Here, you can see more details about this algorithm and how to improve it by using some estimation, thus transforming it into A*.
What’s the Relation Between Graph Search and Artificial Intelligence?
Well, let’s recapitulate what AI is. Like I said before, artificial intelligence is defined as a study of rational agents where a rational agent could be anything that makes decisions like a person, firm, machine, or software. It carries out an action with the best outcome after considering past and current percepts (agent’s perceptual inputs at a given instance).
And what do we get with a graph search algorithm? We get a function, a program, an agent, that, given a graph, an environment, and a start node, by considering past and current percepts, calculates a series of actions for finding the goal node.
Well, we can see here that what a graph search algorithm does fits the definition of an AI agent. So, we have a basic form of AI. You see here, AI is not exactly rocket science. The definition is broad enough to include simple algorithms as the graph search. These examples give us a way to understand the basic concept of AI.
Considering the AI concepts, let’s write an AI agent that analyzes the environment and calculates a series of actions that could help us to reach the goal (we will basically build a graph search algorithm but use AI terminology).
Below is the map of Romania.

Let’s say that we are in Arad and we want to go, on the shortest path, to Bucharest. We can see that there are multiple routes that we can take. We can go from Arad to Timisoara, then Lugoj, and so on, or we can choose Sibiu then Fagaras and go straight to Bucharest. But we don’t know which path has the lowest cost.
What’s the Definition of the Problem?
A problem can be broken down in a number of components:
- We have an initial state: being in Arad
- We have a function actions (s). It returns the set of possible actions when we are in a state. E.g: being in Arad, we can go to Zerind, Sibiu, or Timisoara
- We have a function result (s,a) -> s’ . Being in state s, if we apply the action a, we will go to s’
- We have a goal test function goaltest (s) -> t/f. It tells us if we reached the goal
- step_cost (s,a,s’) -> cost of action. It tells us the step cost from going from s to s’ using the action a
- cost (S1 -> S2 -> … -> Sn) -> n (cost of path). The total path cost
Let’s now see how this maps on our goal-finding problem. The initial state is being in Arad and the goaltest function returns if we reach Bucharest. All the possible states is called the state space. We have to explore the state space by applying actions and going from state to state. Starting with Arad and applying the function actions (“Arad”) we will get three possible actions. Going to Zering, Timisoara, or Sibiu. Now, with this in mind, we can separate the state space into three parts:
- We have the explored part of the state (e.g. just Arad for now)
- We have the frontier. We call this the farthest states that have been explored (Timisoara, Zerind, and Sibiu)
- And the unexplored state: all the other cities
So, being in the explored part of the state, we need to select a new state from the frontier, apply an action, and move to that state, thus expanding the frontier.
TreeSearch(G, s)
s.costSoFar = 0;
for all nodes w in G except s
w.costSoFar = Int.maxInt
Let frontier be a priority queue ordered by the cost_so_far
frontier.enqueue(s)
while (frontier is not empty)
//Removing that vertex from frontier,whose neighbour will be visited now
v = frontier.dequeue()
If v is goal
return “found the goal”
//processing all the neighbours of v
for all neighbours w of v in Graph G
currentCost = dist[v,w]
newCost = v.costSoFar + currentCost;
If (newCost < w.costSoFar) {
w.costSoFar = newCost ;
frontier.enqueue(w)So, we have a frontier that, at first, consists just in the start node. Then, at each iteration, we get the an element from the frontier, we move to the next state, and if we reached the goal, we exit with the message “found the goal”. Optionally, we can also print the path. Otherwise, we add the new states to the frontier.
Now, depending on how you will get the new state from the frontier, you could implement a classic BFS, a uniform cost search, or an A* algorithm. Here, you could see more clearly the differences between these algorithms and the best algorithm for detecting the shortest path from Arad to Bucharest.
Conclusion
Of course, the AI agents don’t resume to just graph search. We have AI algorithms for face recognition, we have machine learning, neural networks, and statistic-based algorithms, where the only limit is mathematics. But this doesn’t have to scare as, as the basic concepts are not that hard to understand.
Further Reading
From Dijkstra to A Star (A*), Part 1: The Dijkstra Algorithm
Graph-Powered Search: Neo4j and Elasticsearch
Opinions expressed by DZone contributors are their own.

Comments