Decoded: Examples of How Hashing Algorithms Work
If cryptography were a car, then the hashing algorithm would be its engine.
Join the DZone community and get the full member experience.
Join For FreeIf cryptography was a body, its hashing algorithm would be the heart of it. If cryptography was a car, its hashing algorithm would be its engine. If cryptography was a movie, its hashing algorithm would be the star. If cryptography was the solar system, its hashing algorithm would be the sun. Okay, that’s probably too far, but you’ve got the point, right? Before we get to the what hashing algorithm is, why it’s there, and how it works, it’s important to understand where its nuts and bolts are. Let’s start with hashing.
What Is Hashing?
Let’s try to imagine a hypothetical situation here. Suppose you want to send a message/file to someone and it is absolutely imperative that it reaches its intended recipient in the exact same format. How would you do it? One option is to send it multiple times and verify that it wasn’t tampered with. But what if the message is too long? What if the file measures in gigabytes? It would be utterly absurd, impractical, and, quite frankly, boring to verify every single letter, right? Well, that’s where hashing comes into play.
Using a chosen hash algorithm, data is compressed to a fixed size. Let’s understand this with an example. If we take the sentence, “Donkeys live a long time” and apply the joaat hash algorithm to it, we will get 6e04f289. This value is known as a hash.
Hashes are highly convenient when you want to identify or compare files or databases. Rather than comparing the data in its original form, it’s much easier for computers to compare the hash values. Whether it’s storing passwords, in computer graphics, or in SSL certificates, hashing does it all.
Fundamentally, hashing is defined by two distinct characteristics – irreversibility and uniqueness. Irreversibility points to the fact that once you hash something, there is no way back. Unlike encryption and encoding, you can’t easily de-hash a message/data. Unique, because no two hash values are ever the same for two different pieces of data. If two hashes are found to be the same for two different pieces of data, it’s called a ‘hash collision’ and that algorithm becomes useless.
(Note: We have used joaat hashing algorithm here as it’s short and easy to comprehend. Modern-day algorithms are much more complex and long.)
Hashing Function: the Core of Hashing Algorithm
“Behind every successful man, there is a great woman.” — Groucho Marx
“Behind every successful hash algorithm, there is a great hash function.” – We just made that up.
Let’s put the jokes aside for a moment and concentrate on the crux of the matter. A hash function is a mathematical function that converts an input value into a compressed numerical value – a hash or hash value. Basically, it’s a processing unit that takes in data of arbitrary length and gives you the output of a fixed length – the hash value.
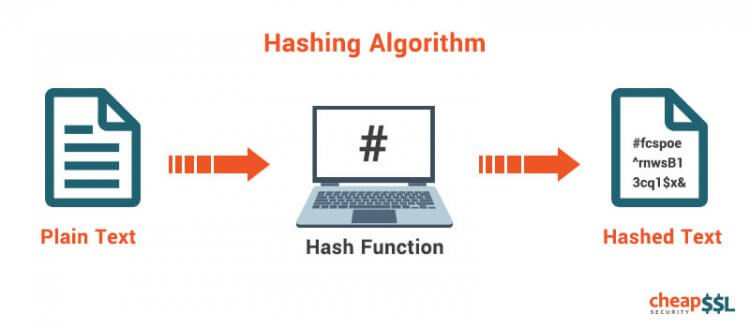
The length of the output or the hash depends on the hashing algorithm. Generally speaking, the most popular hashing algorithms or functions have a hash length ranging from 160 to 512 bits.
Now, let’s move on to the part you’ve been waiting for.
What Is a Hashing Algorithm? How Does it Work?
As we discussed, a hash function lies at the heart of a hashing algorithm. But, to get the hash value of a pre-set length, you first need to divide the input data into fixed sized blocks. This is because a hash function takes in data at a fixed-length. These blocks are called ‘data blocks.’ This is demonstrated in the image below.
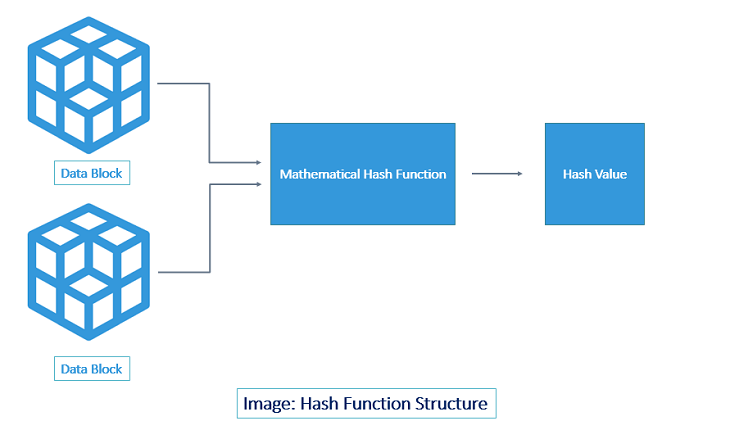
The size of the data block(s) differs from one algorithm to another. But for a particular algorithm, it remains the same. For example, SHA-1 takes in the message/data in blocks of 512-bit only. So, if the message is exactly of 512-bit length, the hash function runs only once (80 rounds in case of SHA-1). Similarly, if the message is 1024-bit, it’s divided into two blocks of 512-bit and the hash function is run twice. However, 99 percent of the time, the message won’t be in the multiples of 512-bit. For such cases (almost all cases), a technique called padding is used. Using a padding technique, the entire message is divided into fixed-size data blocks. The hash function is repeated as many times as the number of data blocks. This is how it’s done:
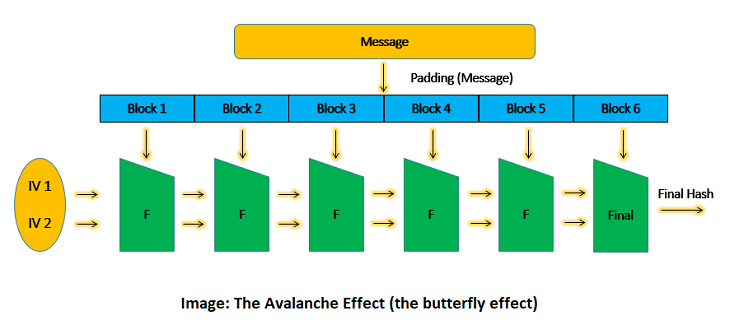 As shown above, the blocks are processed one at a time. The output of the first data block is fed as input along with the second data block. Consequently, the output of the second is fed along with the third block and so on. Thus, we are making the final output the combined value of all the blocks. If you change one bit anywhere in the message, the entire hash value changes. This is called the 'avalanche effect.'
As shown above, the blocks are processed one at a time. The output of the first data block is fed as input along with the second data block. Consequently, the output of the second is fed along with the third block and so on. Thus, we are making the final output the combined value of all the blocks. If you change one bit anywhere in the message, the entire hash value changes. This is called the 'avalanche effect.'
Popular Hashing Algorithms
- Message Digest (MD) Algorithm
- Secure Hash Algorithm (SHA)
- RACE Integrity Primitives Evaluation Message Digest (RIPEMD)
- Whirlpool
- RSA
Published at DZone with permission of Jake Adley. See the original article here.
Opinions expressed by DZone contributors are their own.

Comments