How to draw a Control flow graph & Cyclometric complexity for a given procedure
Join the DZone community and get the full member experience.
Join For Freecyclomatic complexity
cyclomatic complexity is a software metric used to measure the complexity of a program.
this metric measures independent paths through the program's source code. an independent path is defined as a path that has at least one edge which has not been traversed before in any other paths.
cyclomatic complexity can be calculated with respect to functions, modules, methods or classes within a program. 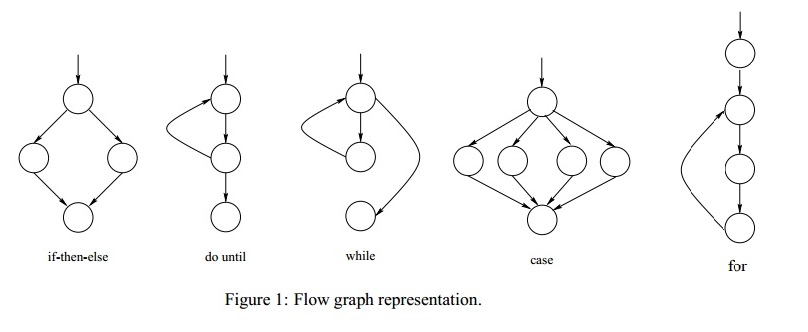
compound condition
where one or more boolean operators such as the logical or, and, nand, nor are present is a conditional statement:
1. if a or b
2. then procedure x
3. else procedure y
4. endif
a predicate node will be created for each statement.
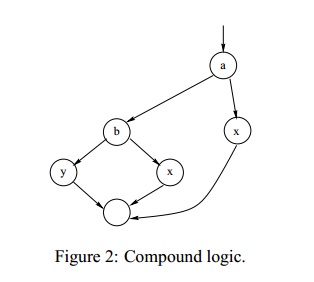
check the following code fragment:
01. insertion_procedure ( int a[], int p [], int n)
02. {
03. int i,j,k;
04. for (i= 0 ; i<=n; i++) p[i] = i;
05. for (i= 2 ; i<=n; i++)
06. {
07. k = p[i];
08. j = 1 ;
09. while (a[p[j- 1 ]] > a[k]) {p[j] = p[j- 1 ]; j--}
10. p[j] = k;
11. }
12. }
first and foremost, start numbering the statement.
01. insertion_procedure ( int a[], int p [], int n)
02. {
03. ( 1 ) int i,j,k;
04. ( 2 ) for ((2a)i= 0 ; (2b)i<=n; (2c)i++)
05. ( 3 ) p[i] = i;
06. ( 4 ) for ((4a)i= 2 ; (4b)i<=n; (4c)i++)
07. {
08. ( 5 ) k=p[i];j= 1 ;
09. ( 6 ) while (a[p[j- 1 ]] > a[k]) {
10. ( 7 ) p[j] = p[j- 1 ];
11. ( 8 ) j--
12. }
13. ( 9 ) p[j] = k;
14. }
now you can clearly see which statement executes first and which executes last, etc. so drawing the cfg becomes simple:

now, to calculate the cyclomatic complexity you use one of three methods:
- count the number of regions on the graph: 4
- no. of predicates (red on graph) + 1 : 3 + 1 = 4
- no of edges – no. of nodes + 2: 14 – 12 + 2 = 4
that’s about it. happy coding :)
Published at DZone with permission of Pubudu Dissanayake. See the original article here.
Opinions expressed by DZone contributors are their own.

Comments