ES6 Math Functions You Can Use Today

as of june 2015, the world has a new javascript standard. officially called ecmascript 2015, but commonly known as ecmascript 6 (es6) and sometimes ecmascript harmony or ecmascript.next, the specifications detail a broad range of new features you can expect to see being implemented in browsers in the coming months and years. this includes—but is not limited to—block-level scoped variables let and const, new class syntax, default parameters, modules, sets, and template strings. it also includes some useful additions to the math object. unlike most new features of es6 at the time of writing, (almost in their entirety) these features have already been implemented in the desktop versions of chrome, firefox, safari, and opera, as well as microsoft edge (though not internet explorer). support in mobile browsers is weaker.

none of these new additions are anything groundbreaking. in fact, it's more about adding basic math functionality that is already present in most popular languages. i still think it's worth taking a look at some of them as they will likely be overlooked in other guides to es6. mdn has simple polyfills for all of them, so if you want to use them on your production site you can, even if you get significant mobile traffic.

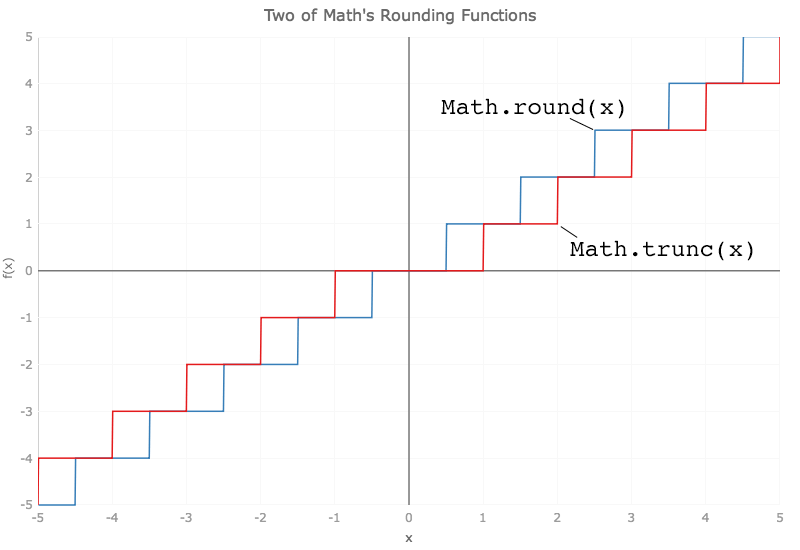
the idea of math.trunc is simple—it removes the digits after the decimal point from a number. 13.2 becomes 13 and -12.6 becomes -12. this is similar to math.ceil and math.floor, except we're not always rounding up or always rounding down, we're rounding towards zero. that is, if the number is positive then math.trunc rounds down but if it is negative it'll round up. the chart below shows how math.trunc and the other rounding function, math.round, work over the range -5 to 5. (plotting math.floor, math.ceil, and math.trunc in the same chart is confusing.)

math.sign is even simpler. pass in a number and it will return 1 if the number is positive (even if that "number" is infinity) and -1 if it is negative (including -infinity). if the number is zero then it will return 0 (or -0, which is the same).

math.cbrt returns the cube root of a number. for positive x, math.cbrt(x) returns the same result as math.pow(x,1/3). however, if x is negative the latter returns nan where as the former will return the same result as -1*math.pow(-x,1/3). for example, math.cbrt(-8) returns -2 while math.pow(-8,1/3) returns nan. this isn't a bug , it's part of the specification . at the same time -2, is a correct solution; all non-zero real numbers, positive and negative, have three cubed roots but two of them are complex . the chart below shows curves for math.cbrt and the (old) square root function math.sqrt. (the square roots of all negative numbers are complex so math.sqrt also returns nan when fed a negative argument.)

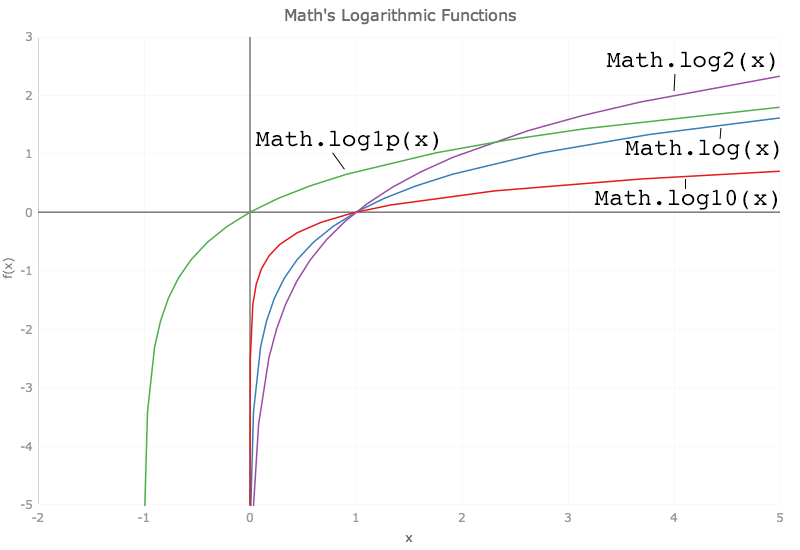
javascript has had the math.log function, that calculates the natural logarithm (that is base-e) of its argument, since the 1st edition of ecmascript. es6 adds math.log10 and math.log2 that calculate the base-10 and base-2 (a.k.a. binary) logarithms of their argument. the former is frequently used in 2d data visualization in the sciences when the numbers being plotted span a large range in one or both dimensions. confusingly, many math text books will use "log" to signify the base-10 logarithm, shortening the natural logarithm to "ln".

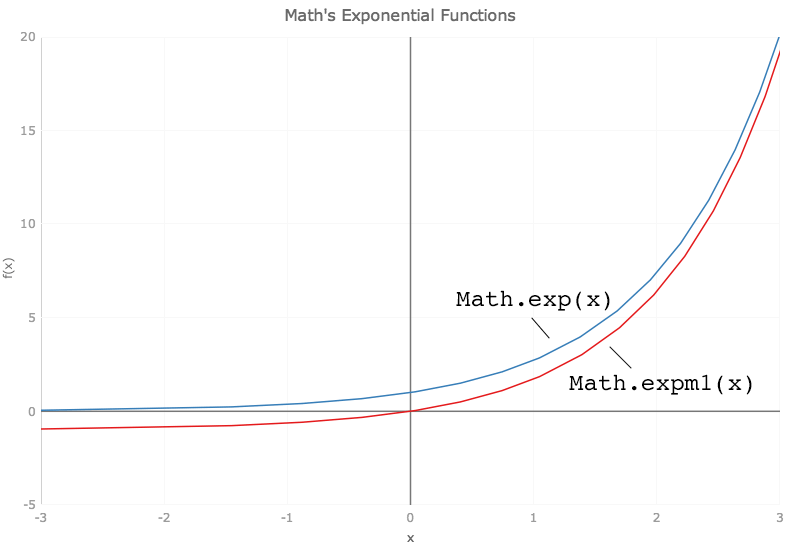
es6 also sees the introduction of math.log1p, which is the same as math.log(1 + x), and math.expm1, which produces the same result as math.exp(x)-1. the chart directly below plots the aforementioned logarithmic functions while the one below that plots math.exp and math.expm1.

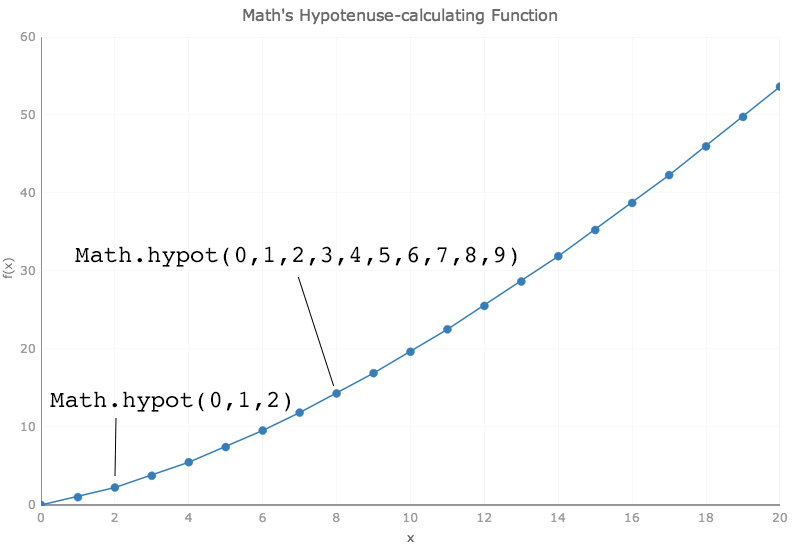
math.hypot calculates the square root of the sum of the squares of its arguments. obviously you can use it to find the hypotenuse of a right triangle if you know the lengths of the other two sides, but you can pass it more than two numbers, or just 1, and it will still calculate the sum of the squares of its arguments. the chart below, for example, shows the result of calling math.hypot for all non-negative integers up to x. for example, the y-value at x=1 is the result of math.hypot(0,1), at x=2 it's the result of math.hypot(0,1,2), at x=3 it's the result of math.hypot(0,1,2,3) and so on.

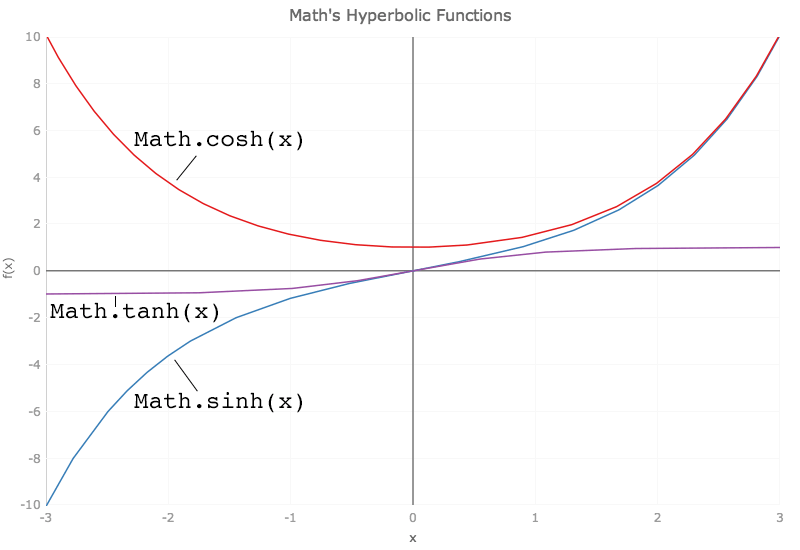
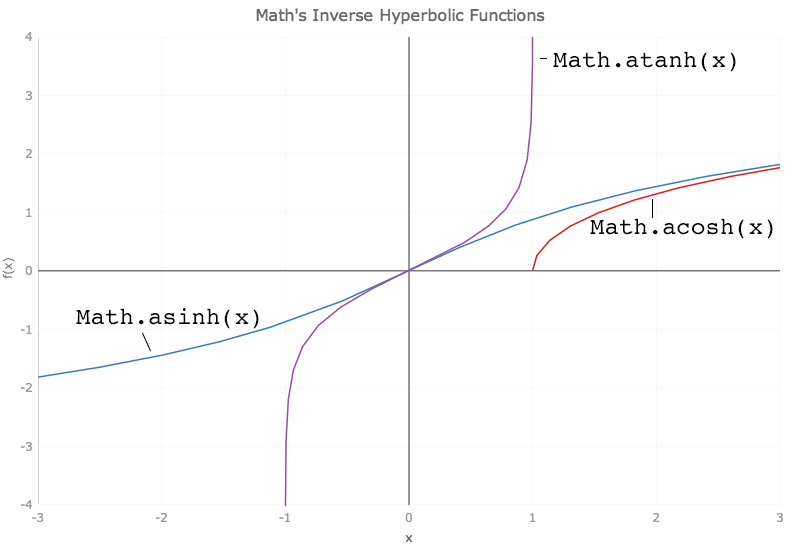
finally, es6 sees the addition of the hyperbolic functions sinh, cosh, and tanh and their inverses asinh, acosh, and atanh. hyperbolic functions are analogs of their similarly named trigonometric counterparts (sin, cos, etc.) and crop up regularly in physics, engineering, and architecture. the chart immediately below plots math.sinh, math.cosh, and math.tanh; the one below that plots their inverses.

there are three further functions added to the math object that, for reasons of brevity, i won't discuss. they are math.imul , math.fround , and math.clz32 .

originally written by tim brock