An Introduction to Bloom Filters
An introduction to the Bloom filter data structure, explaining what it is, when to use it, and key technical details about its implementation and functionality.
Join the DZone community and get the full member experience.
Join For FreeThe Bloom filter is a lesser-known data structure that is not widely used by developers. It is a space-efficient, highly probabilistic data structure that every developer should be familiar with. It can significantly speed up exact match queries, especially in cases where indexing has not been added to that field. The space efficiency of a Bloom filter provides the added advantage of allowing filters to be created for multiple fields.
How It Works
Reading from a database or storage is a costly operation. To optimize this, we use a Bloom filter to check the availability of a key-value pair and only perform a database read if the filter responds with a 'Yes.' Bloom filters are space-efficient and can be stored in memory. Additionally, the lookup test for a value can be performed in O(1) time. More on this later. Let’s explore this concept with an example:

We create a Bloom filter for the key 'Key1'. When clients request data associated with any value of Key1, we first check the availability of the value by passing it through the Bloom filter. In the diagram above, we attempt to read the payload for three different values of Key1:
- For the first value, 'Value1', the filter responds with a 'No,' allowing us to short-circuit the read operation and return "not available."
- In the second example, 'Value2' exists in the database. The filter responds with a 'Yes,' prompting a database read to retrieve the payload associated with Key1 = Value2.
- The third example is more interesting: the filter responds with a 'Yes' for 'Value3,' but the database does not contain any payload for Key1 = Value3. This is known as a false positive. In this case, a database read is performed, but no value is returned.
Although false positives can occur, there are never false negatives — meaning it is impossible for a key-value combination to exist while the filter returns a 'No.'
How to Implement a Bloom Filter
A Bloom filter is a bit array of length 'n,' with all values initialized to 0. It requires 'h' distinct hash functions to populate the bit array. When a value is added to the filter, each hash function is applied to the value to generate a number between 0 and n, and the corresponding 'h' bits are set in the bit array.
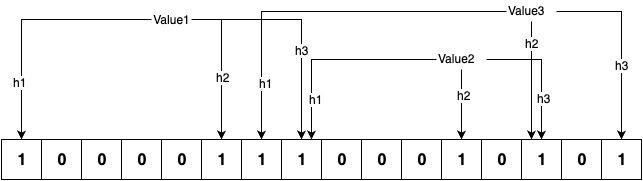
To test whether an element exists in the array, the same set of hash functions is applied to the element, generating 'h' indices between 0 and n. We then check if the corresponding bits in the bit array for those indices are set to 1. If all the bits are set to 1, it is considered a hit, and the filter returns true.
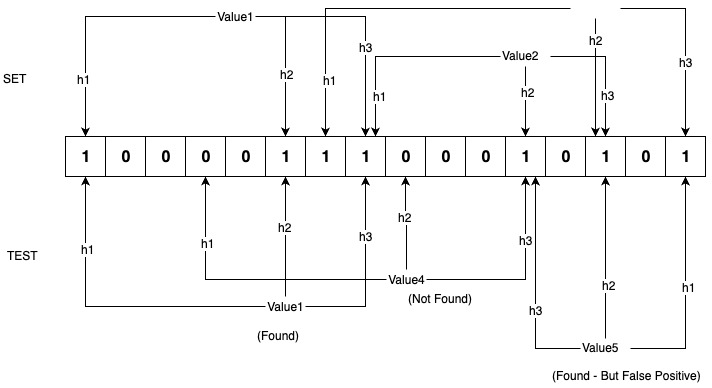
As shown in the above example, Value1, Value2, and Value3 are added to the filter. Each value is passed through three hash functions, and the corresponding bits in the bit array are set. Later, during testing, Value1, Value4, and Value5 are passed through the same set of hash functions to determine whether the values exist.
Due to the nature of hash functions and their finite range of output values, multiple inputs can generate the same hash value, leading to collisions. Collisions can result in false positives, as demonstrated in the case of Value5.
Selecting an appropriate hash function and an adequate length for the bit array can help reduce collisions. Additionally, understanding the range of possible input values, such as all strings or numbers within a finite range, can assist in choosing an optimal hash function and bit array length.
Time and Space Complexity
Hash functions operate in O(1) time, making both the set and test operations constant-time operations. The space required depends on the length of the bit array; however, compared to a traditional index, this space is minimal as the Bloom filter does not store actual values but only a few bits per value.
Limitations
1. Bloom filters can only support exact matches because their operation relies on passing input through hash functions, which require an exact match.
2. Deleting a value from a Bloom filter is not straightforward since bits in the array cannot simply be unset. A bit set in the array may correspond to multiple values. To support deletions, the bit array would need to be recreated.
3. If the hash function(s) and bit array length are not chosen correctly, it may result in an increased number of false positives, making the filter inefficient and potentially an overhead. In the worst-case scenario, all bits in the array could be set after adding all the values. In such a situation, any test would always yield a positive response from the filter. To address this, the filter can be recreated with a resized bit array and new hash functions tailored to better meet the requirements.
Final Thoughts
Hopefully, this article has introduced you to Bloom filters, if you weren’t already familiar with them, and provided you with a valuable data structure to expand your knowledge. Like any other data structure, its usage depends on the specific use case, but it can prove to be highly useful when the right opportunity arises.
Opinions expressed by DZone contributors are their own.

Comments