Metal and the Simulated Annealing Algorithm
The Simulated Annealing algorithm described in this article demonstrates its effectiveness as a powerful tool for finding optimal solutions to complex problems.
Join the DZone community and get the full member experience.
Join For FreeIn this article, I’ll walk you through Bryan Luke’s Simulated Annealing Algorithm, a powerful probabilistic approach to finding optimal solutions among numerous possibilities. We’ll explore its implementation using the classic N-Queens problem as an example. Unlike greedy algorithms, simulated annealing intelligently explores the solution space to avoid being trapped in poor solutions.
What Is Simulated Annealing?
Simulated annealing is inspired by the physical process of annealing metals, where a material is heated and then cooled slowly to improve its internal structure. The algorithm mimics this process to find solutions in complex problem spaces.
Developed in the late 1980s, simulated annealing has become a go-to tool in fields like computer science, engineering, finance, and even biology. It’s especially effective for optimization problems with vast and irregular search spaces.
The Algorithm in Action
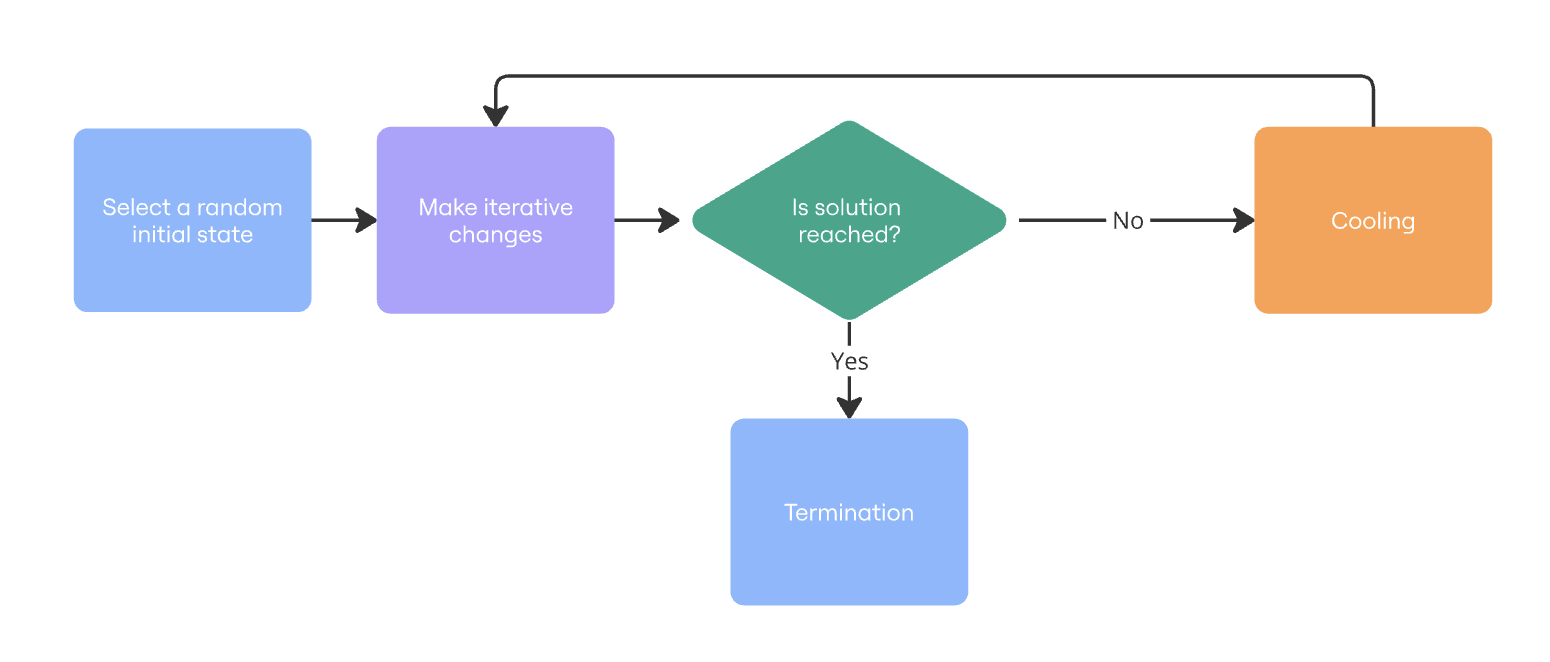
Algorithm Phases
- Initialization: Begin by selecting a random initial state and setting a temperature. The temperature controls the likelihood of accepting new states at each step:
- High temperature: Lower probability of accepting a new state.
- Low temperature: Higher probability of accepting a new state.
- Iterative changes: Make a small, random modification to the current solution to create a new candidate state.
- State evaluation: Compare the new state to the current state. Accept the better state. If the new state is worse, accept it with a probability determined by the formula:
- exp((curScore - newScore) / temperature) >= random[0..1]
- Cooling schedule: Gradually reduce the temperature.
- Termination: End the process when a termination condition is met.
Solution Example Using N-Queens Problem
Let’s explore how this algorithm can solve the N-Queens problem: positioning N queens on an N×N chessboard so that no two queens threaten each other on diagonals, verticals, or horizontals.
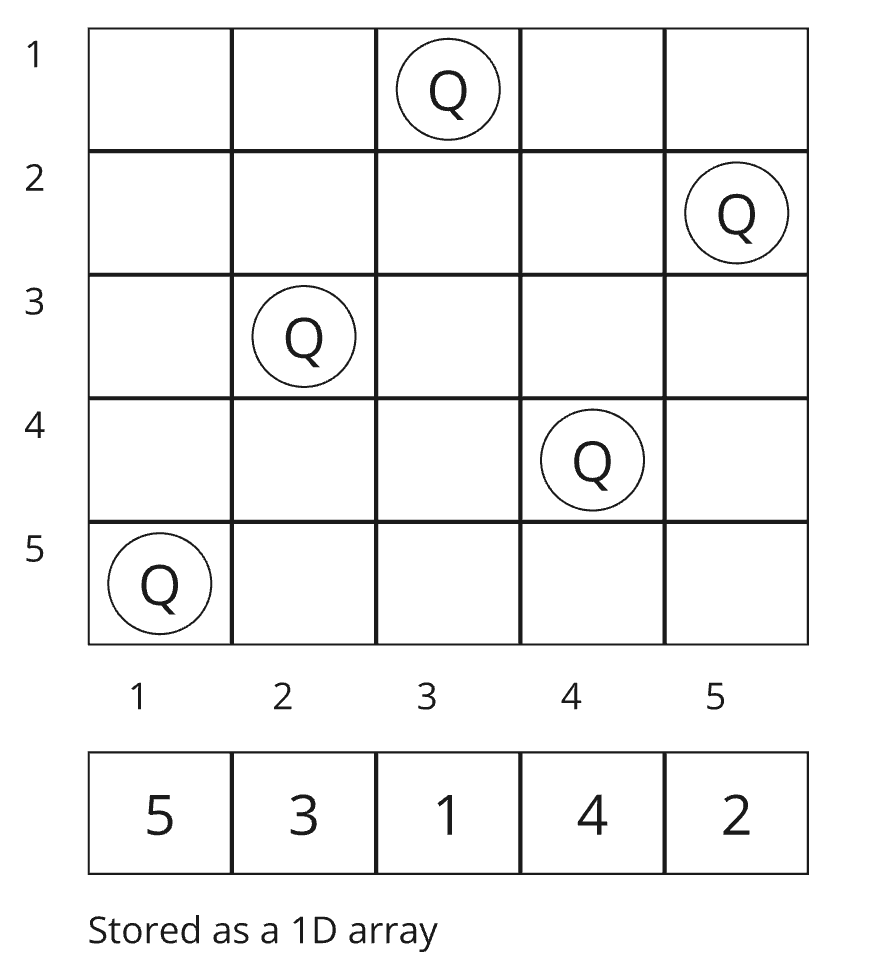
Representing the Board
We’ll represent the chessboard as a 1D array, where each element represents a queen’s position on the Y-axis. Since all values in the array are unique, no queens threaten each other horizontally or vertically.
Evaluating the Board
The goal is to minimize the calculated number of queens that threaten each other. A solution is reached when this number becomes zero.
Generating New States
At each step, swap the positions of two random queens along the X-axis.
Algorithm Implementation in Kotlin
for (temperature in temperatures) {
val new = current.randomSwapQueens()
// acceptNewScore is always true here new.score < current.score
val acceptNewScore = exp((current.score - new.score) / temperature) > Random.nextFloat()
if (acceptNewScore) {
current = new
if (current.score < best.score) {
best = current
if (best.score == 0) { return }
}
}
}
val temperatures = sequence {
var t = 0.7 // initial temperature
while (t > 0.02) { // final temperature
repeat(400) { // steps per change
yield(t) // send t to sequence
}
t *= 0.99 // decreasing coefficient
}
}
val QueenBoard.score get() = this.threatingQueenCountThis solution achieves a runtime of approximately 180 ms for a 100×100 board on an Apple M1 chip.
Conclusion
Simulated annealing is a versatile and powerful algorithm for tackling optimization problems, from finding the shortest path to designing VLSI chips. It’s a testament to how theoretical concepts like physical annealing can be adapted to solve practical challenges in computing and beyond. I hope it inspires you to experiment with other problems and helps you find efficient solutions in your work!
You can find all the source code on GitHub: simulated annealing. For comparison, check out the C-based source code on GitHub: archive data.
Thanks for reading!
Opinions expressed by DZone contributors are their own.

Comments