Recommendation Engine Models

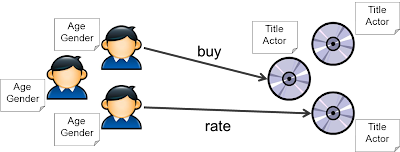
Now given all the metadata of user and item, as well as their interaction over time, can we answer the following questions ...

1. What is the probability that userX purchase itemY ?
2. What rating will userX give to itemY ?
3. What is the top k unseen items that should be recommended to userX ?
   
   

Content-based Approach
In this approach, we make use of the metadata to categorize user and item and then match them at the category level. One example is to recommend jobs to candidates, we can do a IR/text search to match the user's resume with the job descriptions. Another example is to recommend an item that is "similar" to the one that the user has purchased. Similarity is measured according to the item's metadata and various distance function can be used. The goal is to find k nearest neighbors of the item we know the user likes.

Collaborative Filtering Approach
In this approach, we look purely at the interactions between user and item, and use that to perform our recommendation. The interaction data can be represented as a matrix.


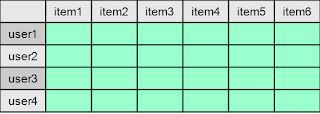
Notice that each cell represents the interaction between user and item. For example, the cell can contain the rating that user gives to the item (in the case the cell is a numeric value), or the cell can be just a binary value indicating whether the interaction between user and item has happened. (e.g. a "1" if userX has purchased itemY, and "0" otherwise.

The matrix is also extremely sparse, meaning that most of the cells are unfilled. We need to be careful about how we treat these unfilled cells, there are 2 common ways ...

• Treat these unknown cells as "0". Make them equivalent to user giving a rate "0". This may or may not be a good idea depends on your application scenarios.
• Guess what the missing value should be. For example, to guess what userX will rate itemA given we know his has rate on itemB, we can look at all users (or those who is in the same age group of userX) who has rate both itemA and itemB, then compute an average rating from them. Use the average rating of itemA and itemB to interpolate userX's rating on itemA given his rating on itemB.
  
  

User-based Collaboration Filter
In this model, we do the following

1. Find a group of users that is “similar” to user X
2. Find all movies liked by this group that hasn’t been seen by user X
3. Rank these movies and recommend to user X

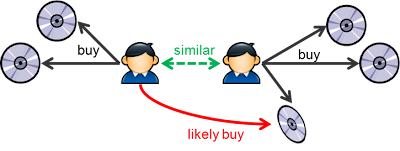
This introduces the concept of user-to-user similarity, which is basically the similarity between 2 row vectors of the user/item matrix. To compute the K nearest neighbor of a particular users. A naive implementation is to compute the "similarity" for all other users and pick the top K.

Different similarity functions can be used. Jaccard distance function is defined as the number of intersections of movies that both users has seen divided by the number of union of movies they both seen. Pearson similarity is first normalizing the user's rating and then compute the cosine distance.

There are two problems with this approach

1. Compare userX and userY is expensive as they have millions of attributes
2. Find top k similar users to userX require computing all pairs of userX and userY
   
   

To resolve problem 1, we approximate the similarity using a cheap estimation function, called minhash. The idea is to find a hash function h() such that the probability of h(userX) = h(userY) is proportion to the similarity of userX and userY. And if we can find 100 of h() function, we can just count the number of such function where h(userX) = h(userY) to determine how similar userX is to userY. The idea is depicted as follows ...


It will be expensive to permute the rows if the number of rows is large. Remember that the purpose of h(c1) is to return row number of the first row that is 1. So we can scan each row of c1 to see if it is 1, if so we apply a function newRowNum = hash(rowNum) to simulate a permutation. Take the minimum of the newRowNum seen so far.

As an optimization, instead of doing one column at a time, we can do it a row at the time, the algorithm is as follows


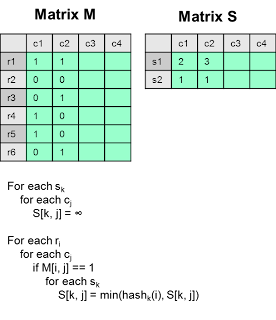
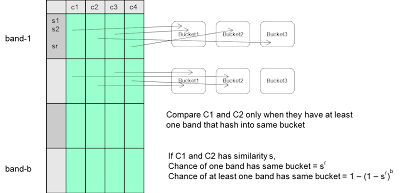
To solve problem 2, we need to avoid computing all other users' similarity to userX. The idea is to hash users into buckets such that similar users will be fall into the same bucket. Therefore, instead of computing all users, we only compute the similarity of those users who is in the same bucket of userX.

The idea is to horizontally partition the column into b bands, each with r rows. By pick the parameter b and r, we can control the likelihood (function of similarity) that they will fall into the same bucket in at least one band.


Item-based Collaboration Filter
If we transpose the user/item matrix and do the same thing, we can compute the item to item similarity. In this model, we do the following ...

1. Find the set of movies that user X likes (from interaction data)
2. Find a group of movies that is similar to these set of movies that we know user X likes
3. Rank these movies and recommend to user X
   
   
   

It turns out that computing item-based collaboration filter has more benefit than computing user to user similarity for the following reasons ...

• Number of items typically smaller than number of users
• While user's taste will change over time and hence the similarity matrix need to be updated more frequent, item to item similarity tends to be more stable and requires less update.
  
  

Singular Value Decomposition
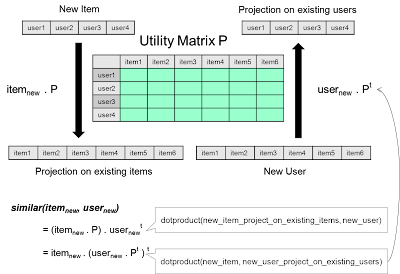
If we look back at the matrix, we can see the matrix multiplication is equivalent to mapping an item from the item space to the user space. In other words, if we view each of the existing item as an axis in the user space (notice, each user is a vector of their rating on existing items), then multiplying a new item with the matrix gives the same vector like the user. So we can then compute a dot product with this projected new item with user to determine its similarity. It turns out that this is equivalent to map the user to the item space and compute a dot product there.


In other words, multiply the matrix is equivalent to mapping between item space and user space. Now lets imagine there is a hidden concept space in between. Instead of jumping directly from user space to item space, we can think of jumping from user space to a concept space, and then to the item space.


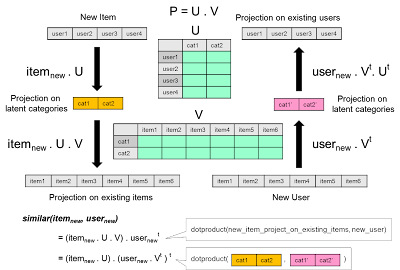
Notice that here we first map the user space to the concept space and also map the item space to the concept space. Then we match both user and item at the concept space. This is a generalization of our recommender. We can use SVD to factor the matrix into 2 parts. Let P be the m by n matrix (m rows and n columns). P = UDV where U is an m by m matrix, each column represents the eigenvectors of P*transpose(P). And V is an n by n matrix with each row represents the eigenvector of transpose(P)*P. D is a diagonal matrix containing eigenvalues of P*transpose(P), or transpose(P)*P. Notice that D can be thought as the strength of each "concept" in the concept space. And the value is order in terms of their magnitude in decreasing order. If we remove some of the weakest concept by making them zero, we reduce the number of non-zero elements in D, which effective generalize the concept space (make them focus in the important concepts).
current_user_tag = alpha * item_tag + (1 - alpha) * prev_user_tag

To recommend an item to the user, we simply need to calculate the top k items by computing the dot product (ie: cosine distance) of the user tag vector and the item tag vector.

Source:  http://horicky.blogspot.com/2011/09/recommendation-engine.html