Understanding Floating-Point Precision Issues in Java

Java Floating Numbers Look Familiar

In Java, we have two types of floating-point numbers: float and double. All Java developers know them but can't answer a simple question described in the following meme:

Are you robot enough?

What Do You Already Know about Float and Double?

float and double represent floating-point numbers. float uses 32 bits, while double uses 64 bits, which can be utilized for the decimal or fractional part. But what does that actually mean? To understand, let's review the following examples:

Intuitive results are completely contradictory and seem to contain mistakes:

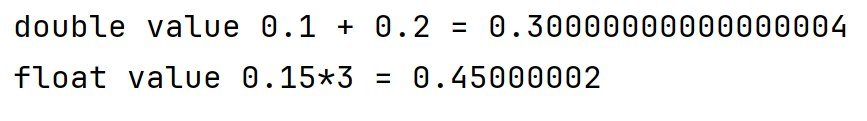But how is this possible? Where do the 4 and 2 at the end of the numbers come from? To understand, let's review how these numbers are actually created.  

Don’t Trust Your Eyes: Reviewing How 0.1 Converted to IEEE Standard

float and double follow the IEEE standard, which defines how to use 32/64 bits to represent a floating-point number. But how is a number like 0.1 converted to a bit array? Without diving too much into the details, the logic is similar to the following:

Converting Floating 0.1 to Arrays of Bits First

In the first stage, we need to convert the decimal representation of 0.1 to binary using the following steps:

1. Multiply 0.1 by 2 and write down the decimal part.
2. Take the fractional part, multiply it by 2, and note the decimal part.  
3. Repeat the first step with the fraction from the second step.  

So for 0.1, we get the following results:

After repeating these steps, we get a binary sequence like 0.0001100110011 (in fact, it’s a repeating infinite sequence).

Converting Binary Array to IEEE Standard

Inside float/double, we don't keep the binary array as it is. float/double follow the IEEE 754 standard. This standard splits the number into three parts:

1. Sign (0 for positive and 1 for negative)
2. Exponent (defines the position of the floating point, with an offset of 127 for float or 1023 for double)
3. Mantissa (the part that comes after the floating point, but is limited by the number of remaining bits)

So now converting 0.0001100110011... to IEEE, we get:

• Sign 0 for positive
• Exponent : Considering first four zeros  0.0001100110011 = -4 + 127 = 123 (or 01111011)
• Mantissa 1100110011 (Mantissa ignores first 1), so we get 100110011

So the final representation is:

So What? How Do These Numbers Explain Weird Results?

After all these conversions, we lose precision due to two factors:

• We lose precision when converting from the infinite binary representation (which has repeating values like 1100110011).
• We lose precision when converting to IEEE format because we consider only the first 32 or 64 bits.

This means that the value we have in float or double doesn't represent exactly 0.1. If we convert the IEEE bit array from float to a "real float," we get a different value. More precisely, instead of 0.1, we get 0.100000001490116119384765625.  

How can we verify this? There are a couple of ways. Take a look at the following code:

And as we expect, we get the following results:

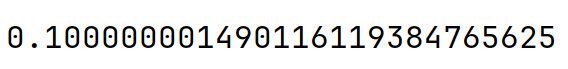
But if we want to go deeper, we can write reverse engineering code:

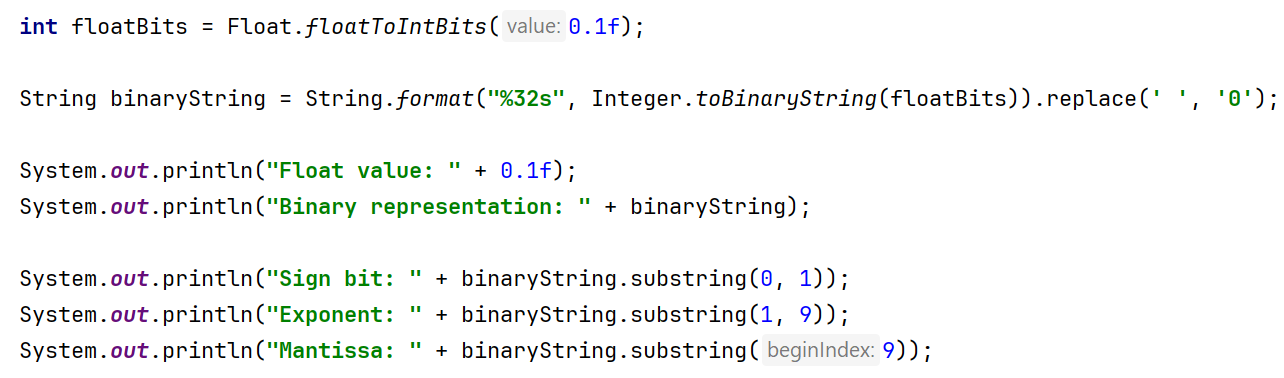
As expected, it confirms our ideas:

Answering the Question and Drawing Conclusions

Now that we know the value we see at initialization is different from what is actually stored in float/double, we expect the value on the left (0.1) but instead, we initialize with the value on the right (0.100000001490116119384765625):

So, knowing this, it's clear that when we perform actions such as adding or multiplying values, this difference becomes more pronounced, until it becomes visible during printing.

Conclusions

Here are the conclusions we can draw:

1. Don’t use floating-point values for precise calculations, such as in finance, medicine, or complex science.
2. Don’t compare two double values for equality directly; instead, check the difference between them with a small delta. For example: boolean isEqual = Math.abs(a - b) < 0.0000001;
3. Use BigDecimal or similar classes for precise calculations.

I hope you now understand why 0.1 + 0.2 returns 0.300000000000004. Thanks for reading!