Adaline Explained With Python Example

In this post, you will learn the concepts of Adaline (ADAptive LInear NEuron), a machine learning algorithm, along with a Python example. Like Perceptron, it is important to understand the concepts of Adaline as it forms the foundation of learning neural networks. The concept of Perceptron and Adaline could found to be useful in understanding how gradient descent can be used to learn the weights which when combined with input signals is used to make predictions based on unit step function output.

Here are the topics covered in this post in relation to Adaline algorithm and its Python implementation:

• What's Adaline?
• Adaline Python implementation
• Model trained using Adaline implementation

What's Adaline?

Adaline, like Perceptron, also mimics a neuron in the human brain. You may want to read one of my related posts on Perceptron — Perceptron explained using Python example. Adaline is also called as single-layer neural network. Here is the diagram of Adaline:

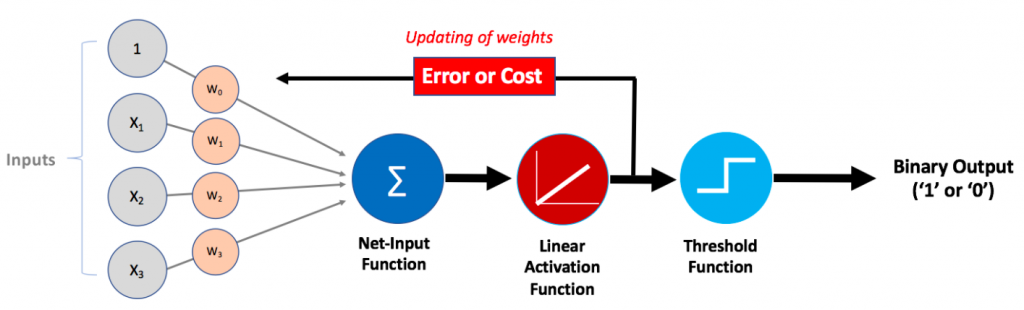
The following represents the working of Adaline machine learning algorithm based on the above diagram:

• Net Input function - Combination of Input signals of different strength (weights): Input signals of different strength (weights) get combined / added in order to be fed into the activation function. The combined input or sum of weighted inputs can also be called as net input.  Pay attention to the Net-input function shown in the above diagram
• Net input is fed into activation function (Linear): Net input is fed into activation function. The activation function of adaline is an identity function. If Z is net input, the identity function would look like \(g(Z) = Z\). The activation function is linear activation function as the output of the function is linear combination of input signals and weights.
• Activation function output is used to learn weights: The output of activation function (same as net input owing to identity function) is used to calculate the change in weights related to different inputs which will be updated to learn new weights. Pay attention to feedback loop shown with text Error or cost. Recall that in Perceptron, the activation function is a unit step function and the output is binary (1 or 0) based on whether the net input value is greater than or equal to zero (0) or otherwise.
• Threshold function - Binary prediction (1 or 0) based on unit step function: The prediction made by Adaline neuron is done in the same manner as in case of Perceptron. The output of activation function, which is net input is compared with 0 and the output is 1 or 0 depending upon whether the net input is greater than or equal to 0. Pay attention in the above diagram as to how the output of activation function is fed into threshold function.

Adaline Python Implementation

The adaline algorithm explained in previous section with the help of diagram will be illustrated further with the help of Python code. Here are the algorithm steps and the related Python implementation:

• Weighted input signals combined as net input: First step is to combine the input signals with respective weights (strength of input signals) and come up with sum of weighted inputs. This is also termed as net input.

'''

Net Input is sum of weighted input signals

'''

def net_input(self, X):

      weighted_sum = np.dot(X, self.coef_[1:]) + self.coef_[0]

      return weighted_sum

• Activation function invoked with net input: Net input is fed into activation function to calculate the output. The activation function is a linear activation function. It is an identity function. Thus, \(g(Z) = Z\). Note that the output or return value of activation function is same as input (identity function)

xxxxxxxxxx

'''

Activation function is fed the net input. As the activation function is

an identity function, the output from activation function is same as the

input to the function.

'''

def activation_function(self, X):

      return X

• Prediction based on unit step function: Prediction is made based on the unit step function which provides binary output as 1 or 0 based on whether the output of activation function is greater than or equal to zero. If the output of activation function is greater than or equal to zero, the prediction is 1 or else 0. Note how activation function is invoked with net input and the output of activation function is compared with 0.

xxxxxxxxxx

'''

Prediction is made on the basis of output of activation function

'''

def predict(self, X):

  return np.where(self.activation_function(self.net_input(X)) >= 0.0, 1, 0)

• Weights learned using activation function output (continuous value): Unlike Perceptron where weights are learned based on the prediction value which is derived as out of unit step function, the weights in case of Adaline is learned by comparing the actual / expected value with the out of activation function which is a continuous value. Note that the weights are learned based on batch gradient descent algorithm which requires the weights to be updated after considering the weight updates related to all training examples. This is unlike stochastic gradient descent where weights are updated after each training example.

xxxxxxxxxx

Batch Gradient Descent 

1. Weights are updated considering all training examples.

2. Learning of weights can continue for multiple iterations

3. Learning rate needs to be defined

'''

def fit(self, X, y):

    rgen = np.random.RandomState(self.random_state)

    self.coef_ = rgen.normal(loc=0.0, scale=0.01, size=1 + X.shape[1])

    for _ in range(self.n_iterations):

          activation_function_output = self.activation_function(self.net_input(X))

          errors = y - activation_function_output

          self.coef_[1:] = self.coef_[1:] + self.learning_rate*X.T.dot(errors)

          self.coef_[0] = self.coef_[0] + self.learning_rate*errors.sum()

Here is the entire Python code of Adaline algorithm custom implementation:

xxxxxxxxxx

class CustomAdaline(object):

    def __init__(self, n_iterations=100, random_state=1, learning_rate=0.01):

        self.n_iterations = n_iterations

        self.random_state = random_state

        self.learning_rate = learning_rate

    '''

    Batch Gradient Descent 

    1. Weights are updated considering all training examples.

    2. Learning of weights can continue for multiple iterations

    3. Learning rate needs to be defined

    '''

    def fit(self, X, y):

        rgen = np.random.RandomState(self.random_state)

        self.coef_ = rgen.normal(loc=0.0, scale=0.01, size=1 + X.shape[1])

        for _ in range(self.n_iterations):

              activation_function_output = self.activation_function(self.net_input(X))

              errors = y - activation_function_output

              self.coef_[1:] = self.coef_[1:] + self.learning_rate*X.T.dot(errors)

              self.coef_[0] = self.coef_[0] + self.learning_rate*errors.sum() 

    '''

    Net Input is sum of weighted input signals

    '''

    def net_input(self, X):

            weighted_sum = np.dot(X, self.coef_[1:]) + self.coef_[0]

            return weighted_sum

    '''

    Activation function is fed the net input. As the activation function is

    an identity function, the output from activation function is same as the

    input to the function.

    '''

    def activation_function(self, X):

            return X

    '''

    Prediction is made on the basis of output of activation function

    '''

    def predict(self, X):

        return np.where(self.activation_function(self.net_input(X)) >= 0.0, 1, 0) 

    '''

    Model score is calculated based on comparison of 

    expected value and predicted value

    '''

    def score(self, X, y):

        misclassified_data_count = 0

        for xi, target in zip(X, y):

            output = self.predict(xi)

            if(target != output):

                misclassified_data_count += 1

        total_data_count = len(X)

        self.score_ = (total_data_count - misclassified_data_count)/total_data_count

        return self.score_

Model Trained With Adaline Algorithm

Here is the Python code which represents the breast cancer classification model trained using Adaline implementation explained in the previous section:

xxxxxxxxxx

#

# Load the data set

#

bc = datasets.load_breast_cancer()

X = bc.data

y = bc.target

#

# Create training and test split

#

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42, stratify=y)

#

# Instantiate CustomPerceptron

#

adaline = CustomAdaline(n_iterations = 10)

#

# Fit the model

#

adaline.fit(X_train, y_train)

#

# Score the model

#

adaline.score(X_test, y_test), prcptrn.score(X_train, y_train)

The score of the model on the test data set turns out to be around 0.63.

Conclusions

Here is the summary of what you learned in this post in relation to Adaline algorithm and its Python implementation:

• Adaline algorithm mimics a neuron in the human brain
• Adaline is similar to the algorithm Perceptron. It can also be termed as a single-layer neural network.
• The difference between Adaline and Perceptron lies in the manner in which weights are learned based on the differences between the output label and the continuous value output of the activation function. In Perceptron, the difference between an actual label and a predicted label is used to learn the weights.