logging is a fundamental part of applications. every application has a varying flavor of logging mechanism. a well designed logging system is a huge utility for system administrators and developers, especially the support team. logs save many valuable hours for both the support team or developers. as users execute programs at the front end, the system invisibly builds a vault of event information (log entries) for system administrators and the support team.
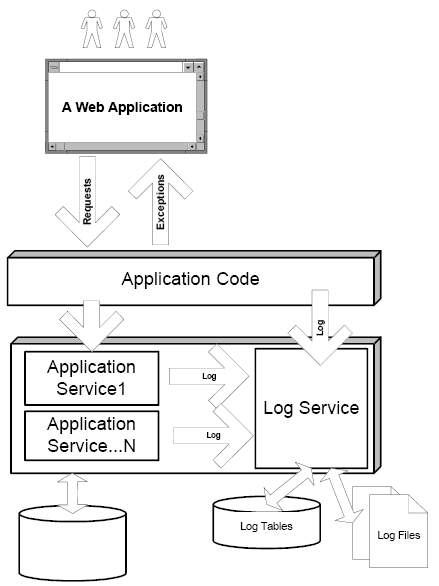
after stating its value, let’s try to figure out the logging requirements for an application. java has a standard logging api in its new versions (java.util.logging). log4j is also a well-known library for logging. we implemented a transparent “logging service” in our application framework. you may prefer some kind of logging implementations but there are some other important questions you have to answer in your application design which are
what
to log,
when
to log,
how much
to log,
how to control
logging and how
correlate
it with your exception system.
what to log
some application exceptions should be logged:
why not log all exceptions? some exceptions are managed exceptions which are thrown by application as a warning or as a validation error to the user. if all validation errors or application exceptions are included in logs, the logs will lose their usefulness. it would contain many entries, it makes it hard to reach valuable entries. here, we should discriminate exceptions if they should be logged.
we used a loggable mark interface to determine if it is included in logs. another best practice is to have a single global exception handler. in this way, application developers don’t worry about logging of any exception they generate. a single exception handler means a single unified and neat exception logging mechanism.
some application events should be logged:
for major components of an application we may log lifecycle events like start, stop and restart. some security-related events may be logged such as unauthorized url access attempts, user logins etc. some resource thresholds may be exceeded and should also be logged.
some application states should be logged:
in some codes, we should ask that “what could go wrong here in this code”. if this state occurs, we may throw an exception or log it (if we don’t want to interrupt current process) with some levels like error, warning or information. for example if a connection is normally released while it is uncommitted, that info may be logged as uncommitted connection release that points some application code problems.
some debug information may be logged:
in some applications, you may have some errors and can’t find why this is happening. you may add some debug logs into your code and redeploy it to diagnose the problem. some chronic bugs deserve debug traces which can’t be detected in development environment.
executed sqls may be logged:
in some conditions, we may want to get the sql statement executed by an application. we should easily switch logging on without start/stop of system. let’s say user complain about wrong report result when executing a report. if we don’t have a clue about that we may log sql and trace it.
user http requests may be logged:
we may need what is coming from the user with full parameter details. to achieve this kind of logging we have to plug a log service in servlets and jsp pages.
executing threads may be logged:
i mentioned a blackbox implementation in our applications in one of my previous posts. you may log executing thread information to that black box to figure out what may go wrong in a system crash.
javascript errors may be logged:
this may be considered same with first item but its implementations totally differs. you need to have a global javascript exception handler. in the handler, you submit javascript error with ajax to log on the server (assuming it is not an ajax error).
some best practices
as i said above, the exception handling system is an important plug point for logging. in all our servlets and jsps, the main code blocks have the following structure to enable global exception handling. this standard eliminates the work of logging exceptions by developers (transparent unified logging):
try
{
}
catch(exception e)
{
globalhandler.handleexception(e);
}
we named “log medium” to mean where to store log entries but in java logging api it is called handlers. for some type of logs, database logs are handy since you can run powerful sql queries against log table which is merely possible in files.
to assign log messages to the appropriate log levels is also important. otherwise some wrong alerts would mislead system administrators.
we used system.err stream for application-level logging which is same place with e.printstacktrace() which may be printed with our global handler log entry at the same time. we wouldn’t need all exception’s stack trace but some may be very useful to see where the root of the problem (i.e. stackoverflowexception).
when logging exceptions we used following format. some articles recommends that we’d better to include problem failover suggestion but i think this information should be given to the user not included in the logs. logs are rarely read but exceptions are in front of users.
log entry should answer following questions:
who
(username)
, when
(timestamp)
, where
(context, servletorpage,database)
, what
(command)
, result
(exception)
[errorhandlername] username: userabc databasename: abc timestamp: 15.07.2009 13:02:08 context:servlet page: /prod/sales/salesorders.jsp window: windwname command: savesalesorder exception: shortdescriptionofexception
exceptionstacktracehere
in a clustered environment, logging should be considered. we separated same type of log files with a cluster node name suffix to the file name. otherwise, concurrent log writes may lead to some problems. system_node01.log system_node02.log
as a last item, logging may be a very interesting performance killer. if applications begin to log a lot, application performance may severely fall down. i have a real life story for that. once we had forgotten to include an image file in deployment package. it was being used in every page. when we started system after installment, page response was so slow. log files seem small enough that may not incur problem. after, opening and reading log files, we realized that log frequency (stating image is missing) was high and that was causing the problem. in conclusion, your log file size and log writing frequency should be small.


Comments