Understanding Binary Trees Part 1

Quick recap of some basic tree vocabulary, before getting in depth into this series of Binary Trees... 

What Is a Tree?

Unlike Arrays, Linked Lists, Stack, and Queues, which are linear data structures, trees are hierarchical data structures. Trees represent non-linear data structures and can be defined as collection of entities called “Nodes” linked together to simulate hierarchy. In other words, Tree is a widely used abstract data type (ADT) that simulates a hierarchical tree structure

Important Tree Glossary:

• Root: Node without any parent. Topmost node of a tree
• Children: Immediate successor nodes
• Siblings: Children of same parent
• Leaf node: Any node that doesn’t have any children
• Internal Nodes: All nodes with at least one child
• Depth of Node x: Length of path from root to Node x
• Height of Node x: Number of edges in the longest path from node x to leaf node
• Height of tree: Height of the tree is the height of the root
• Level of node: Set of all nodes at a given depth is called the level of the tree

Key Properties:

• Trees with N nodes will have N-1 edges
• Depth of root node is Zero
• Root node is at level Zero
• Height of leaf node is Zero
• Height of tree with one node is Zero
• Every node except root is connected by a directed edge from exactly one node to other node and direction is: parent -> children

Now, having understood the fundamentals of trees, let us get into this series of Binary Trees

So, What Is a Binary Tree?

A tree is called a binary tree if each node has either 

• Zero,
• One, or 
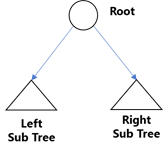
• Two children

An empty tree is also a valid binary tree. 

We can visualize a binary tree as consisting of a root and two disjoint binary trees called left and right subtrees of the root.

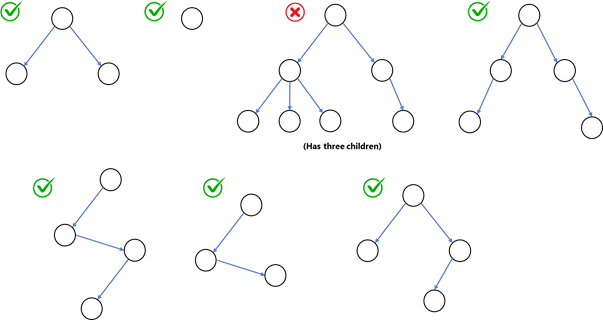
Examples of Binary trees:

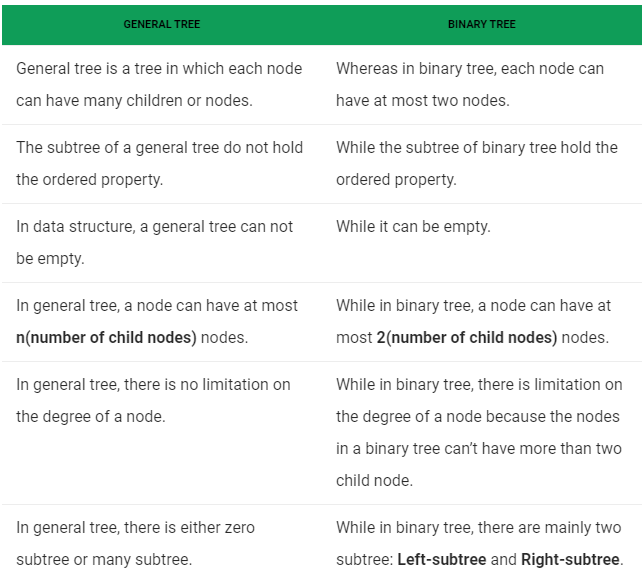
Difference between a Tree and Binary Tree:

Properties of Binary Tree      

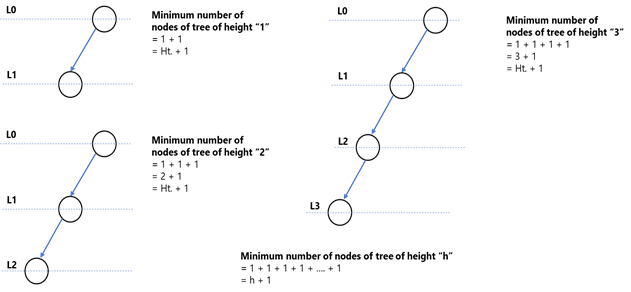
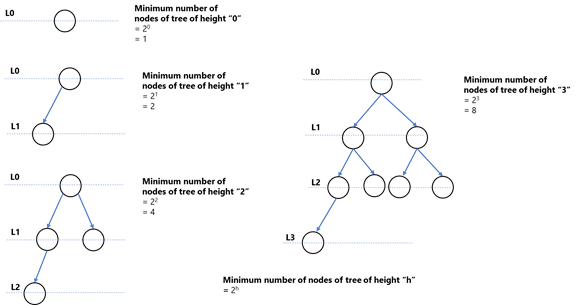
• Maximum number of nodes of binary tree of height “h” is 2^h+1 - 1

• Minimum number of nodes of binary tree of height “h” is “h+1”

• Minimum height of the binary tree of with maximum number of nodes as “n”  

For any binary tree of height “h”, maximum number of nodes = 2^h+1 – 1
Here, Max nodes = n
So, n = 2^h+1 – 1

=> n + 1 = 2^h+1 

Applying log on both sides,

=>log(n+1) = log2^h+1 

=> log(n+1) = (h+1) log2

=>log(n+1)=(h+1)

=>Height of the binary with maximum “n” nodes => h = ⌈ log(n+1) ⌉ - 1

• Minimum height of the binary tree of with maximum number of nodes as “n” 

For any binary tree of height “h”, minimum number of nodes = h + 1

=>n=h+1

=>Height of the binary with minimum “n” nodes => h = n-1

Types of Binary Trees

The following are common types of Binary Trees:

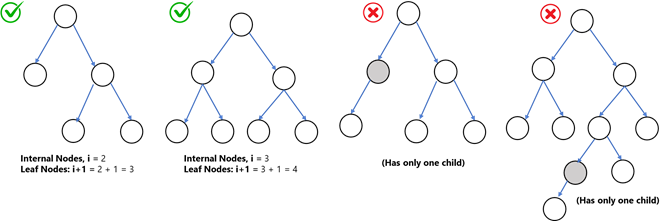
Full/Strict Binary Trees:

A full binary tree is called a binary tree in which each node has exactly

• Zero or
• Two children

• In a full binary tree, number of leaf nodes = No. of internal nodes + 1

Properties of full binary tree:

• Maximum number of nodes of full binary tree of height “h” is 2^h+1 – 1
• Minimum number of nodes of full binary tree of height “h” is 2h+1

• Minimum height of the full binary tree of with maximum number of nodes as “n” is ⌈ log(n+1) ⌉ - 1
• Maximum height of the binary tree of with minimum number of nodes as “n”

For any binary tree of height “h”, minimum number of nodes = 2h + 1

=>n=2h+1

=>Height of the binary with minimum “n” nodes => h = (n-1)/2

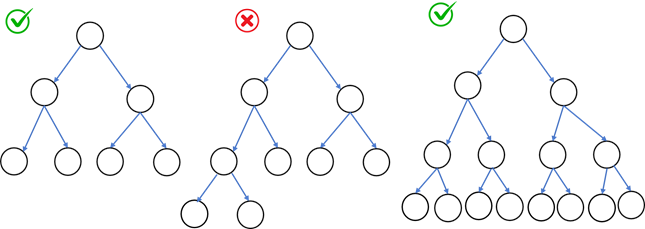
Complete Binary Tree

A binary tree is called a complete binary tree if all levels except possibly the last is completely filled and all the nodes in the last level are as left as possible.

Examples of complete binary trees:

Properties of complete binary tree:

• Maximum number of nodes of complete binary tree of height “h” is 2^h+1 – 1
• Minimum number of nodes of complete binary tree of height “h” - 2^h 

• Minimum height of complete binary tree of with maximum number of nodes as “n” ⌈ log(n+1) ⌉ - 1
• Maximum height of complete binary tree of with minimum number of nodes as “n”

For any binary tree of height “h”, minimum number of nodes = 2^h

=>log(n) = log2^h

=> log(n) = (h)log2

=>h = log(n)

=>Height of the binary with minimum “n” nodes => h = log(n)

To conclude, 

If maximum and minimum nodes are given, height of the tree is 

Perfect Binary Tree

A binary tree is called perfect if all the internal nodes have two children (exactly two children) and all the leaf nodes are at same level. A perfect binary tree can also be a full binary tree or a complete binary tree but not vice versa.

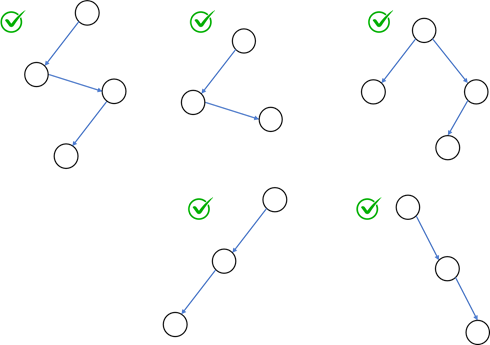
Degenerate Binary Tree

• All the internal nodes have only one child except leaf nodes. 
• If every node in the tree has only one left child, it is left skewed
• If every node in the tree has only one right child, it is right skewed

Balanced Binary Tree

A balanced binary tree is a binary tree structure in which the left and right sub-trees of every node differ in height by no more than 1. Balanced Binary Search trees like AVL Trees, Red-Black Trees are some of the examples

So, in this part, we have understood basic concepts of trees, binary tree, its properties and types. In my next upcoming article, we go deeper into binary tree concepts, applications, traversals, representations and implementations.

Stay tuned!!!