Creating Artificial Doubt Significantly Improves AI Math Accuracy
LLMs are better at math with a "verified reasoning trajectory" — an opportunity to review their steps and determine if the math they're doing makes sense.
Join the DZone community and get the full member experience.
Join For FreeWhat makes an AI system good at math? Not raw computational power, but something that seems almost contradictory: being neurotically careful about being right.
When AI researchers talk about mathematical reasoning, they typically focus on scaling up — bigger models, more parameters, and larger datasets. But in practice, mathematical ability isn’t about how much compute you have for your model. It’s actually about whether machines can learn to verify their own work, because at least 90% of reasoning errors come from models confidently stating wrong intermediate steps.
I guess this sounds obvious once you understand it. Any mathematician would tell you that the key to solving hard problems isn’t raw intelligence — it’s methodical verification. Yet for years, AI researchers have been trying to brute-force mathematical ability by making models bigger, as if sheer computational power alone would produce careful reasoning.
Microsoft’s rStar-Math (the top AImodels.fyi question-answering paper this week) changes this pattern through three linked innovations: code verification of each reasoning step, a preference model that learns to evaluate intermediate thinking, and a multi-round self-evolution process. Their 7B parameter model — using these techniques — matches or exceeds the performance of models 100 times larger.
The system works by forcing explicit verification at every step. Each piece of mathematical reasoning must be expressed as executable code that either runs correctly or fails. This creates a kind of artificial doubt, which serves as a healthy skepticism that prevents unjustified leaps. But verification alone isn’t enough, and the system also needs to learn which reasoning approaches work better than others, which it does through its preference model. And it needs to improve over time, which it achieves through multiple rounds of self-training.
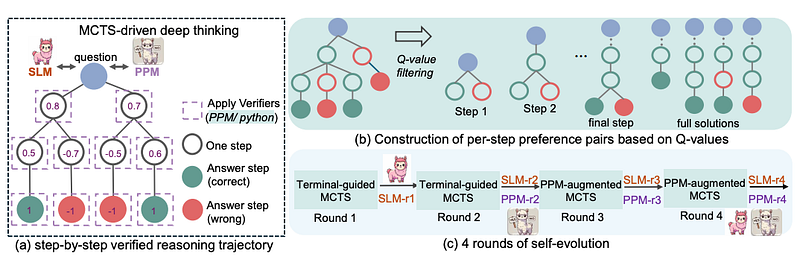 Overview of rStar-math. Note the verified reasoning trajectory module.
Overview of rStar-math. Note the verified reasoning trajectory module.
- Each reasoning step is expressed as a short snippet of Python code that must run correctly.
- A “process preference model” rates each step.
- The system goes through multiple rounds of training, where each iteration builds on the verified solutions from the last one.
I suspect that this constant feedback loop forces the smaller model to “think out loud” in verifiable steps rather than simply guessing. This matches a pattern we’re seeing across the ML world right now, focusing on performance gains through chain-of-thought patterns. OpenAI’s o1 is the most salient example of this, but I’ve covered a lot of other papers that look at similar approaches.
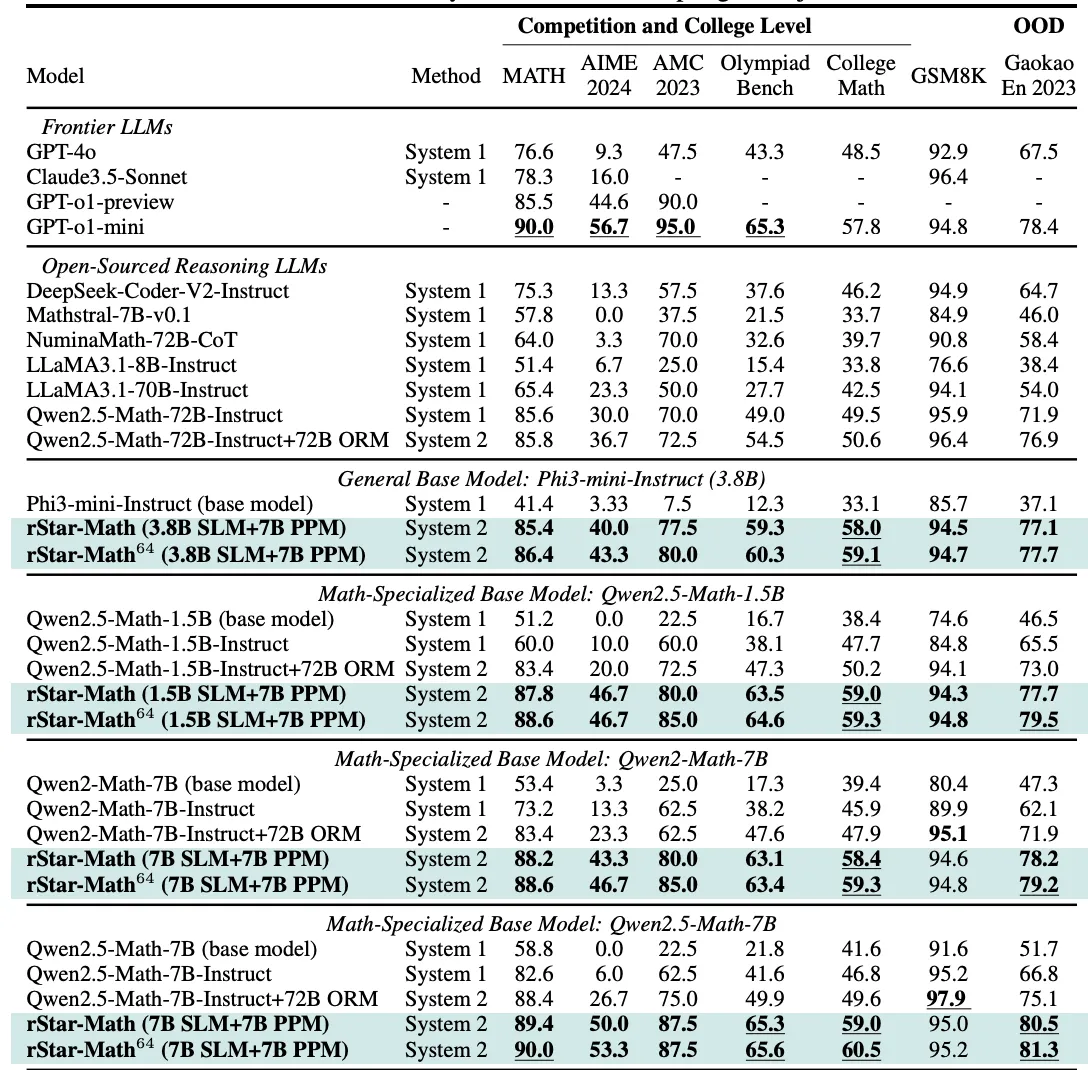
Table 5: The results of rStar-Math and other frontier LLMs on the most challenging math benchmarks. rStar-Math64 shows the Pass@1 accuracy achieved when sampling 64 trajectories.” — from the paper.
Anyway, by the final round, this smaller model apparently scores 90% on the MATH benchmark and solves 53% of real Olympiad-level AIME problems — enough to place it in the top 20% of human contestants. I would have expected results like this to require a model with far more parameters. But rStar-Math suggests that bigger isn’t always better if the system can verify each step and reject faulty paths early.
What’s exciting to me is how this might generalize. For math, code execution is a clean verification signal: either the code runs correctly, and the outputs line up with the partial result, or it doesn’t. In other domains — like law, vaccine research, or creative art tasks — there isn’t an obvious yes/no test for every step. However, I imagine we could still create domain-specific checks or preference models that identify whether each piece of reasoning is reliable. If so, smaller models might compete with or even surpass larger ones in many specialized tasks as long as each reasoning step gets validated.
Some might worry that code-based verification is limited and maybe ask, “How do we scale that to every problem?” But I think we’ll see creative expansions of this approach. For example, a legal model could parse relevant statutes or test arguments against known precedents, and a medical model might consult a knowledge base or run simulations of standard treatments. We could even apply these ideas to everyday tasks as long as we build robust checks for correctness.
Where else can you see this approach being useful? Let me know in the comments. I’d love to hear what you have to say.
Published at DZone with permission of Mike Young. See the original article here.
Opinions expressed by DZone contributors are their own.

Comments