How to Use NumPy to Hadamard Product

The first time you see matrices, if someone asked you how you multiply two matrices together, your first idea might be to multiply every element of the first matrix by the element in the same position of the corresponding matrix, analogous to the way you add matrices.

But that's not usually how we multiply matrices. That notion of multiplication hardly involves the matrix structure; it treats the matrix as an ordered container of numbers, but not as a way of representing a linear transformation. Once you have a little experience with linear algebra, the customary way of multiplying matrices seems natural, and the way that may have seemed natural at first glance seems kinda strange.

The componentwise product of matrices is called the Hadamard product or sometimes the Schur product. Given two m by n matrices A and B, the Hadamard product of A and B, written A ∘ B, is the m by n matrix C with elements given by:

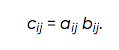
Because the Hadamard product hardly uses the linear structure of a matrix, you wouldn't expect it to interact nicely with operations that depend critically on the linear structure. And yet we can give a couple theorems that do show a nice interaction, at least when A and B are positive semi-definite matrices.

The first is the Schur product theorem. It says that if A and B are positive semi-definite n by n matrices, then

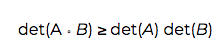
where det stands for determinant.

Also, there is the following theorem of Pólya and Szegö. Assume A and B are symmetric positive semi-definite n by n matrices. If the eigenvalues of A and B, listed in increasing order, are α and β respectively, then for every eigenvalue λ of A ∘ B, we have

α₁ β₁ ≤ λ ≤ α_n β_n.

Python Implementation

If you multiply two (multidimensional) arrays in NumPy, you'll get the componentwise product. So if you multiply two matrices as arrays you'll get the Hadamard product, but if you multiply them as matrices you'll get the usual matrix product. We'll illustrate that below. Note that the function eigvalsh returns the eigenvalues of a matrix. The name may look a little strange, but the "h" on the end stands for "Hermitian." We're telling NumPy that the matrix is Hermitian so it can run software specialized for that case [1].

from numpy import array, matrix, array_equal, all
from numpy.linalg import det, eigvalsh

    A = array([
        [3, 1],
        [1, 3]
    ])

    B = array([
        [5, -1],
        [-1, 5]
    ])

    H = array([
        [15, -1],
        [-1, 15]
    ])

    AB = array([
        [14,  2],
        [ 2, 14]
    ])

    # Hadamard product
    assert(array_equal(A*B, H))

    # Ordinary matrix product
    assert(array_equal(A@B, AB))

    # Schur product theorem
    assert(det(H) >= det(A)*det(B))

    # Eigenvalues
    eigA = eigvalsh(A)
    eigB = eigvalsh(B)
    eigH = eigvalsh(A*B)

    lower = eigA[0]*eigB[0]
    upper = eigA[1]*eigB[1]
    assert(all(eigH >= lower))
    assert(all(eigH <= upper))

The code above shows that the eigenvalues of A are [2, 4], the eigenvalues of B are [4, 6], and the eigenvalues of A ∘ B are [14, 16].

Note

[1] For complex matrices, Hermitian means conjugate symmetric, which in the real case reduces to simply symmetric. The theorem of Pólya and Szegö is actually valid for Hermitian matrices, but I simplified the statement for the case of real-valued matrices.