Norm of a One-Dimensional Tensor in Python Libraries
Learn how to calculate the Euclidean (norm/distance) of a single-dimensional (1D) tensor in NumPy, SciPy, Scikit-Learn, TensorFlow, and PyTorch.
Join the DZone community and get the full member experience.
Join For FreeThe calculation of the norm of vectors is essential in both artificial intelligence and quantum computing for tasks such as feature scaling, regularization, distance metrics, convergence criteria, representing quantum states, ensuring unitarity of operations, error correction, and designing quantum algorithms and circuits.
You will learn how to calculate the Euclidean (norm/distance), also known as the L2 norm, of a single-dimensional (1D) tensor in Python libraries like NumPy, SciPy, Scikit-Learn, TensorFlow, and PyTorch.
Understand Norm vs Distance
Before we begin, let's understand the difference between Euclidean norm vs Euclidean distance.
- Norm is the distance/length/size of the vector from the origin (0,0).
- Distance is the distance/length/size between two vectors.
Prerequisites
- Install Jupyter.
- Run the code below in a Jupyter Notebook to install the prerequisites.
# Install the prerequisites for you to run the notebook
!pip install numpy
!pip install scipy
%pip install torch
!pip install tensorflowYou will use Jupyter Notebook to run the Python code cells to calculate the L2 norm in different Python libraries.
Let's Get Started
Now that you have Jupyter set up on your machine and installed the required Python libraries, let's get started by defining a 1D tensor using NumPy.
NumPy
NumPy is a Python library used for scientific computing. NumPy provides a multidimensional array and other derived objects.

Tensor ranks
# Define a single dimensional (1D) tensor
import numpy as np
vector1 = np.array([3,7]) #np.random.randint(1,5,2)
vector2 = np.array([5,2]) #np.random.randint(1,5,2)
print("Vector 1:",vector1)
print("Vector 2:",vector2)
print(f"shape & size of Vector1 & Vector2:", vector1.shape, vector1.size)Print the vectors
Vector 1: [3 7]
Vector 2: [5 2]
shape & size of Vector1 & Vector2: (2,) 2Matplotlib
Matplotlib is a Python visualization library for creating static, animated, and interactive visualizations. You will use Matplotlib's quiver to plot the vectors.
# Draw the vectors using MatplotLib
import matplotlib.pyplot as plt
%matplotlib inline
origin = np.array([0,0])
plt.quiver(*origin, vector1[0],vector1[1], angles='xy', color='r', scale_units='xy', scale=1)
plt.quiver(*origin, vector2[0],vector2[1], angles='xy', color='b', scale_units='xy', scale=1)
plt.plot([vector1[0],vector2[0]], [vector1[1],vector2[1]], 'go', linestyle="--")
plt.title('Vector Representation')
plt.xlim([0,10])
plt.ylim([0,10])
plt.grid()
plt.show()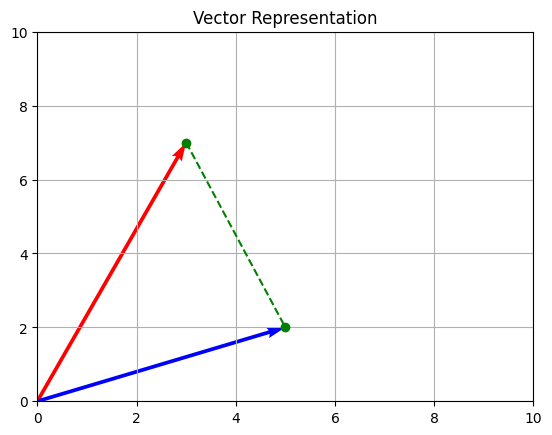
Vector representation using Matplolib
# L2 (Euclidean) norm of a vector
# NumPy
norm1 = np.linalg.norm(vector1, ord=2)
print("The magnitude / distance from the origin",norm1)
norm2 = np.linalg.norm(vector2, ord=2)
print("The magnitude / distance from the origin",norm2)The output once you run this in the Jupyter Notebook:
The magnitude / distance from the origin 7.615773105863909
The magnitude / distance from the origin 5.385164807134504SciPy
SciPy is built on NumPy and is used for mathematical computations. If you observe, SciPy uses the same linalg functions as NumPy.
# SciPy
import scipy
norm_vector1 = scipy.linalg.norm(vector1, ord=2)
print("L2 norm in scipy for vector1:", norm_vector1)
norm_vector2 = scipy.linalg.norm(vector2, ord=2)
print("L2 norm in scipy for vector2:", norm_vector2)Output:
L2 norm in scipy for vector1: 7.615773105863909
L2 norm in scipy for vector2: 5.385164807134504Scikit-Learn
As the Scikit-learn documentation says:
Scikit-learnis an open source machine learning library that supports supervised and unsupervised learning. It also provides various tools for model fitting, data preprocessing, model selection, model evaluation, and many other utilities.
We reshape the vector as Scikit-learn expects the vector to be 2-dimensional.
# Sklearn
from sklearn.metrics.pairwise import euclidean_distances
vector1_reshape = vector1.reshape(1,-1)
## Scikit-learn expects the vector to be 2-Dimensional
euclidean_distances(vector1_reshape, [[0, 0]])[0,0]Output
7.615773105863909TensorFlow
TensorFlow is an end-to-end machine learning platform.
# TensorFlow
import os
os.environ['TF_CPP_MIN_LOG_LEVEL'] = '1'
import tensorflow as tf
print("TensorFlow version:", tf.__version__)
## Tensorflow expects Tensor of types float32, float64, complex64, complex128
vector1_tf = vector1.astype(np.float64)
tf_norm = tf.norm(vector1_tf, ord=2)
print("Euclidean(l2) norm in TensorFlow:",tf_norm.numpy())Output
The output prints the version of TensorFlow and the L2 norm:
TensorFlow version: 2.15.0
Euclidean(l2) norm in TensorFlow: 7.615773105863909PyTorch
PyTorch is an optimized tensor library for deep learning using GPUs and CPUs.
# PyTorch
import torch
print("PyTorch version:", torch.__version__)
norm_torch = torch.linalg.norm(torch.from_numpy(vector1_tf), ord=2)
norm_torch.item()The output prints the PyTorch version and the norm:
PyTorch version: 2.1.2
7.615773105863909Euclidean Distance
Euclidean distance is calculated in the same way as a norm, except that you calculate the difference between the vectors before passing the difference - vector_diff, in this case, to the respective libraries.
# Euclidean distance between the vectors
import math
vector_diff = vector1 - vector2
# Using norm
euclidean_distance = np.linalg.norm(vector_diff, ord=2)
print(euclidean_distance)
# Using dot product
norm_dot = math.sqrt(np.dot(vector_diff.T,vector_diff))
print(norm_dot)Output
Output using the norm and dot functions of NumPy libraries:
5.385164807134504
5.385164807134504# SciPy
from scipy.spatial import distance
distance.euclidean(vector1,vector2)Output Using SciPy
5.385164807134504
The Jupyter Notebook with the outputs is available on the GitHub repository. You can run the Jupyter Notebook on Colab following the instructions on the GitHub repository.
Opinions expressed by DZone contributors are their own.

Comments