Reshaping PyTorch Tensors
This article is an analysis of the hidden design used to reshape PyTorch tensors. What is going on under the hood with n-dimensional tensors in PyTorch?
Join the DZone community and get the full member experience.
Join For FreeIt is a reasonable thing to expect n-dimensional tensor to have a possibility to be reshaped. Reshape means to change the spatial size of a container that holds underlying data. One can create any n-dimensional tensor that wraps a numerical array as long as the product of dimensions stays equal to the number of the array’s elements.
import torch
# underlying data
data = [1,2,3,4,5,6,7,8] # has 8 elements
# two ways to store identical data
tens_A = torch.tensor(data).reshape(shape=(2,4)) # 2-dimensional tensor of shape (2,4)
tens_B = torch.tensor(data).reshape(shape=(2,2,2)) # 3-dimensional tensor of shape (2,2,2)The same holds for reshaping. It’s possible to convert the existing container to a different spatial size while it preserves the total number of elements.
import torch
data = [1,2,3,4,5,6,7,8]
# Original tensor of shape 2x4
tens_A = torch.tensor(data).reshape(shape=(2,4))
# Reshaped from 2x4 to 2x2x2 (preserving number of elements)
tens_B = tens_A.reshape(shape=(2,2,2))This is quite intuitive. But, the experienced users might notice a couple of not obvious things.
- Will the reshaped tensor point to the same underlying data or will the data be copied?
- How to find where elements with known previously indices do live in a new container?
The answer to the first question is that reshaped tensor sometimes triggers copying of underlying data and sometimes doesn’t. The documentation says the following about reshape method:
Returns a tensor with the same data and number of elements as input, but with the specified shape. When possible, the returned tensor will be a view of input. Otherwise, it will be a copy. Contiguous inputs and inputs with compatible strides can be reshaped without copying, but you should not depend on the copying vs. viewing behavior.
This quote introduces three things: the view of a tensor, the stride of a tensor, and contiguous tensors. Let’s talk about them in order.
Stride
Stride is a tuple of integers each of which represents a jump needed to perform on the underlying data to go to the next element within the current dimension. The tensor’s underlying data is just a one-dimensional physical array, that is stored sequentially in the memory. If we have, for example, an arbitrary 3-dimensional container, then the elements at indices (x,y,z) and at(x+1,y,z) live at a distance of size stride(0) within the underlying data. See the code below:
import torch
# Tensor of interest
tens_A = torch.rand((2,3,4)) # 3-dimensional tensor of shape (2,3,4)
# Start index
x = 0
y = 1
z = 3
# Translation from n-dimensional index to offset in the underlying data
offset = tens_A[x,y,z].storage_offset()
# The magnitude of a jump
jump = tens_A.stride(0) # or tens_A.stride()[0]
# Underlying 1d data
data = tens_A.storage()
# Add the jump to the offset of index (x,y,z)
# and compare against the element at index (x+1,y,z)
print(tens_A.storage()[offset + jump] == tens_A[x+1,y,z]) # it is TrueUsing all the stride entries we can translate any given n-dimensional index to the offset within a physical array by ourselves. Here’s the graphical interpretation of a stride. This image is cherry-picked from ezyang’s blog, one of the core PyTorch maintainers.
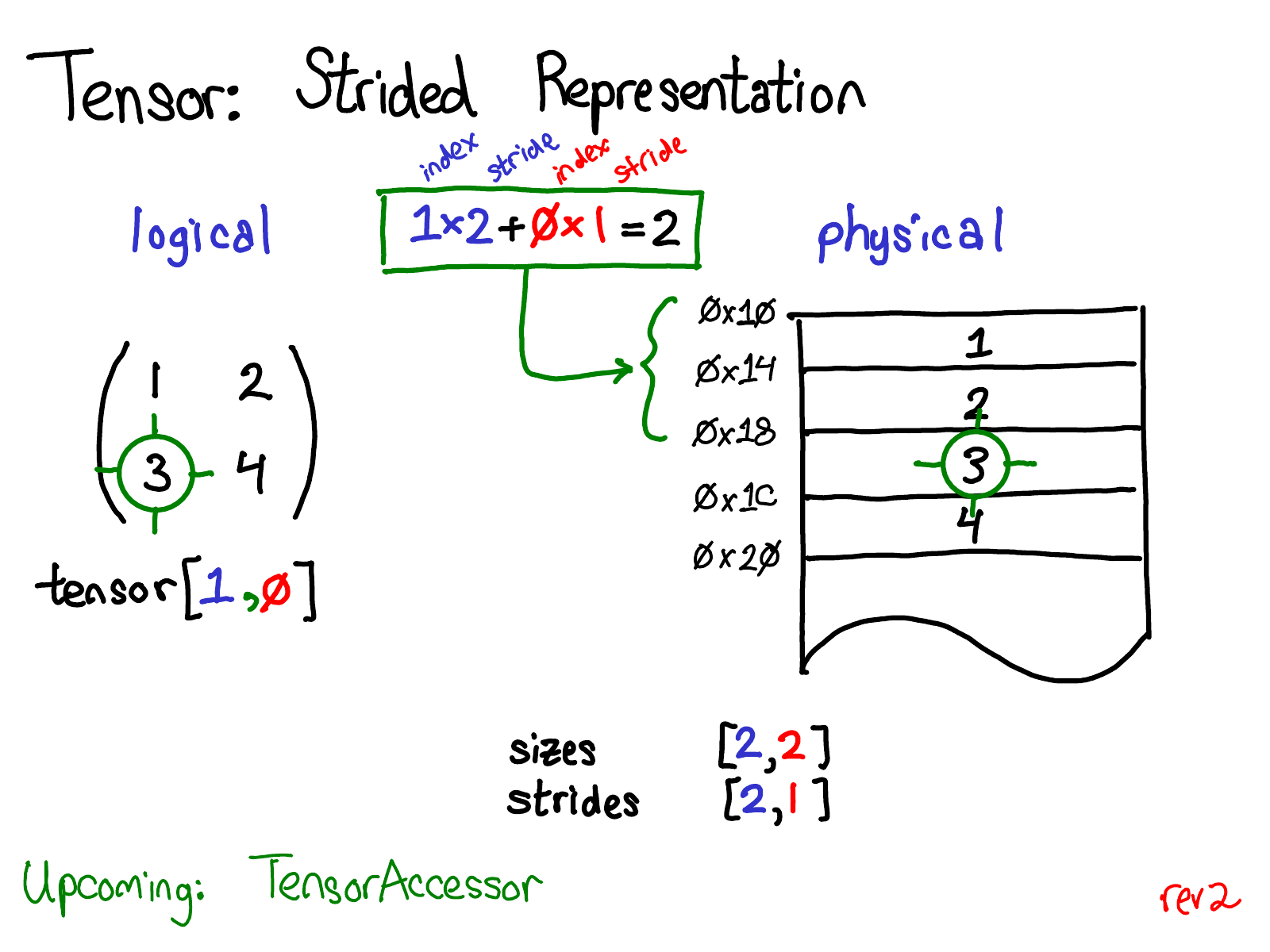
In the picture above, you can see how the index (1,0) inside a 2-by-2 logical tensor translates to the offset of a value 2 within a physical array using strides.
Contiguous Tensor
First, consider a one-dimensional array. One might say it is contiguous if the entries are stored sequentially without any spaces in between. Visualizations from this StackOverflow answer will help us:


Then, consider a multi-dimensional array. A special case is two dimensions, 2d array is contiguous if the underlying data is stored row-wise sequentially.
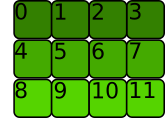

We can generalize that by saying the n-dimensional array is contiguous if its (n-1)-dimensional components are contiguous and stored sequentially in memory.
Finally, we can say that a PyTorch tensor is contiguous if the n-dimensional array it represents is contiguous.
Remark. By “contiguous” we understand “C contiguous”, i.e. the way arrays are stored in language C. There’s also a “Fortran contiguous” alternative when the arrays are stored in column-wise order.
One can deduce the contiguity from the tensor strides. If we take an arbitrary n-dimensional tensor that is contiguous then each stride in the tuple is the product of the corresponding tail of tensor sizes. As in the example:
import torch
# Tensor of interest
tens_A = torch.rand((2,3,4)) # 3-dimensional tensor of shape (2,3,4)
sizes = tens_A.shape
print(tens_A.is_contiguous()) # outputs: True
print(tens_A.stride()) # outputs: (12,4,1)
print(tens_A.stride() == (sizes[1]*sizes[2], sizes[2], 1)) # outputs: TrueLoss and Restoration of Contiguity
Another interesting aspect is that some of the view operators return a new tensor object based on the same underlying data but treat it in a non-contiguous way. For example, transposition. But there’s a way of restoring contiguity using the method contiguous on a tensor, which might trigger copying if the tensor was non-contiguous.
Contiguity is crucial when reshaping is performed. If the tensor is not contiguous then reshape will silently trigger data copying which is not efficient but in some cases it's unavoidable.
import torch
# Tensor of interest
tens_A = torch.rand((2,3,4)) # 3-dimensional tensor of shape (2,3,4)
# Transposed tensor
transp_A = tens_A.t()
# Check contiguity
print(transp_A.is_contiguous()) # output: False
# Make contiguous
tens_B = transp_A.contiguous() # triggers copying because wasn't contiguous
print(tens_B.is_contiguous()) # output: True
# Reshaping
resh_transp_A = transp_A.reshape(shape=(2,2,2,3)) # triggers copying
resh_tens_B = tens_B.reshape(shape=(2,2,2,3)) # won't trigger copyingThe code above shows the cases when the copying happens silently because of non-contiguous order.
View
This method is aimed to reshape tensor efficiently, when possible. That means to use underlying data without explicit copying. The reshape itself is performed by updating the shape and stride of a tensor. The rule of thumb is the following the tensor could be reshaped by view if it is_contiguous==True.
Let’s have a look at this example:
import torch
# Tensor of interest
tens_A = torch.rand((2,3,4)) # 3-dimensional tensor of shape (2,3,4)
def test_view(tensor, sizes):
try:
tensor.view(*sizes)
except Exception as e:
print(e)
print(f"View was Failed: tensor.is_contiguos == {tensor.is_contiguous()}")
else:
print(f"View was Successful: tensor.is_contiguos == {tensor.is_contiguous()}")
sizes = (3,4,2)
# Let's try to use view
test_view(tens_A, sizes)
# Apply view-function that change contiguity and try again
perm_tens_A = tens_A.permute(0,2,1) # change order of axis
test_view(perm_tens_A, sizes) # this will result in RuntimeError("Use .reshape(...) instead")Here are two tests. The one on contiguous tensor and the other on non-contiguous, it is seen that in the latter case view is impossible and it recommends us to use reshape instead.
Summarizing
Here it is! That much theory we need to correctly interpret the documentation on reshape function. And we are ready to answer the first question stated at the beginning: does reshape explicitly copy underlying data?
Reshape method applied on a tensor will try to invoke the view method if it is possible, if not then the tensor data will be copied to be contiguous, i.e. to live in the memory sequentially and to have proper strides, and after this manipulation, it will invoke the view.
Frankly speaking, I cannot fully understand documentation on view method. It is unclear for me what they mean by saying: “…size must be compatible with its original size and stride, i.e., each new view dimension must either be a subspace of an original dimension, or only span across original dimensions…” . If you have any ideas please tell in comments
The Second Question
It is might be clear now that indexing within a reshaped tensor hardly relies on the stride. When we perform reshaping or view the tensor shape and stride properties change. This two are sufficient to deduce where the elements do live after the modification.
Conclusion
In this short article, I tried to accumulate the knowledge on tensor reshaping in PyTorch, the thing that sometimes arise nagging questions during my day-to-day work. It is obvious that copying of underlying memory is bad and it is better to have reshaping without it, but sometimes one might come across it when it happens silently (for example on transposed tensors). Of course, you can learn the use-cases when there’s a place to be, but from my perspective, it is better to understand hidden design, which is quite elegant.
In the next article, I’d like to talk about broadcasting with tensors: how it works and when it is not efficient.
Credits
Opinions expressed by DZone contributors are their own.

Comments