Learning Neural Networks Using Java Libraries
Learn about the evolution of neural networks and get a summary of popular Java neural network libraries in this short guide to implementing neural networks from scratch.
Join the DZone community and get the full member experience.
Join For FreeAs developers, we are used to thinking in terms of commands or functions. A program is composed of tasks, and each task is defined using some programming constructs. Neural networks differ from this programming approach in the sense that they add the notion of automatic task improvement, or the capability to learn and improve similarly to the way the brain does. In other words, they try to learn new activities without task-specific programming.
Instead of providing a tutorial on writing a neural network from scratch, this tutorial will be about neural nets incorporating Java code. The evolution of neural nets starts from McCulloch and Pitt’s neuron, enhancing it with Hebb’s findings, implementing the Rosenblatt’s perceptron, and showing why it can’t solve the XOR problem. We will implement the solution to the XOR problem by connecting neurons, producing a Multilayer Perceptron, and making it learn by applying backpropagation. After being able to demonstrate a neural network implementation, a training algorithm, and a test, we will try to implement it using some open-source Java ML frameworks dedicated to deep learning: Neuroph, Encog, and Deeplearning4j.
The early model of an artificial neuron was introduced by the neurophysiologist Warren McCulloch and logician Walter Pitts in 1943. Their paper, entitled, “A Logical Calculus Immanent in Nervous Activity,” is commonly regarded as the inception of the study of neural networks. The McCulloch-Pitts neuron worked by inputting either a 1 or 0 for each of the inputs, where 1 represented true and 0 represented false. They assigned a binary threshold activation to the neuron to calculate the neuron’s output.
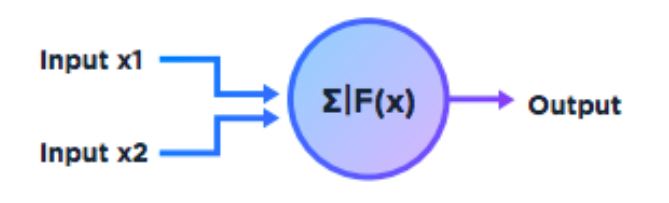
The threshold was given a real value, say 1, which would allow for a 0 or 1 output if the threshold was met or exceeded. Thus, in order to represent the AND function, we set the threshold at 2.0 and come up with the following table:
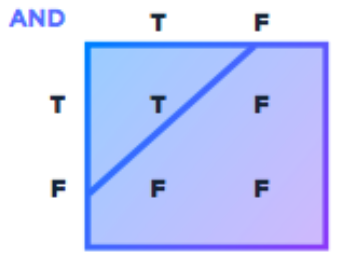
This approach could also be applied for the OR function if we switch the threshold value to 1. So far, we have classic linearly separable data as shown in the tables, as we can divide the data using a straight line. However, the McCulloch-Pitts neuron had some serious limitations. In particular, it could solve neither the “exclusive or” function (XOR) nor the “exclusive nor” function (XNOR), which seem to be not linearly separable. The next revolution was introduced by Donald Hebb, well-known for his theory on Hebbian learning. In his 1949 book, The Organization of Behavior, he states:
“When an axon of cell A is near enough to excite a cell B and repeatedly or persistently takes part in firing it, some growth process or metabolic change takes place in one or both cells such that A’s efficiency, as one of the cells firing B, is increased.”
In other words, when one neuron repeatedly assists in firing another, the axon/connection of the first neuron develops synaptic knobs or enlarges them if they already exist in contact with the second neuron. Hebb was not only proposing that when two neurons fire together the connection between the neurons is strengthened — which is known as the weight assigned to the connections between neurons — but also that this activity is one of the fundamental operations necessary for learning and memory. The McCulloch-Pitts neuron had to be altered to assign weight to each of the inputs. Thus, an input of 1 may be given more or less weight, relative to the total threshold sum.
Later, in 1962, the perceptron was defined and described by Frank Rosenblatt in his book, Principles of Neurodynamics. This was a model of a neuron that could learn in the Hebbean sense through the weighting of inputs and that laid the foundation for the later development of neural networks. Learning in the sense of the perceptron meant initializing the perceptron with random weights and repeatedly checking the answer after the activation was correct or there was an error. If it was incorrect, the network could learn from its mistake and adjust its weights.
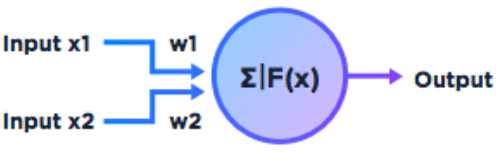
Despite the many changes made to the original McCulloch-Pitts neuron, the perceptron was still limited to solving certain functions. In 1969, Minsky co-authored with Seymour Papert, Perceptrons: An Introduction to Computational Geometry, which attacked the limitations of the perceptron. They showed that the perceptron could only solve linearly separable functions and had not solved the limitations at that point. As a result, very little research was done in the area until the 1980s. What would come to resolve many of these difficulties was the creation of neural networks. These networks connected the inputs of artificial neurons with the outputs of other artificial neurons. As a result, the networks were able to solve more difficult problems, but they grew considerably more complex. Let’s consider again the XOR problem that wasn’t solved by the perceptron. If we carefully observe the truth tables, we can see that XOR turns to be equivalent to OR and NOT AND functions representable by single neurons.
Let’s take a look at the truth tables again:
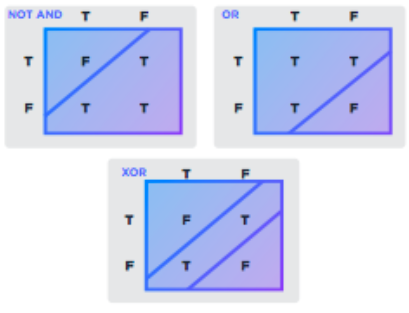
We can combine the two neurons representing NOT AND and OR and build a neural net for solving the XOR problem similar to the net presented below:
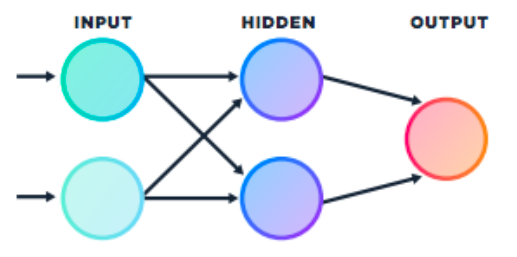
The diagram represents a multiplayer perception, which has one input layer, one hidden layer, and an output layer. The connections between the neurons have associated weights not shown in the picture. Similar to the single perception, each processing unit has a summing and activation component. It looks pretty simple but we also need a training algorithm in order to be able to adjust the weights of the various layers and make it learn. With the simple perception, we could easily evaluate how to change the weights according to the error. Training a multilayered perception implies calculation of the overall error of the network.
In 1986, Geoffrey Hinton, David Rumelhart, and Ronald Williams published a paper, “Learning Representations b yBackpropagating Errors,” which describes a new learning procedure, backpropagation. The procedure repeatedly adjusts the weights of the connections in the network so as to minimize a measure of difference between the actual output vector of the net and the desired output vector. Asa result of the weight adjustments, internal hidden units — which are not part of the input or output — are used to represent important features, and the regularities of the tasks are captured by the interaction of these units.
It’s time to code a multilayered perceptron able to learn the XOR function using Java. We need to create a few classes, like a neuron interface named ProcessingUnit, Connection class, a few more activation functions, and a neural net with a layer that is able to learn. The interfaces and classes can be found in a project located in my GitHub repository.
The NeuralNet class is responsible for the construction and initialization of the layers. It also provides functionality for training and evaluation of the activation results. If you run the NeuralNet class solving the classical XOR problem, it will activate, evaluate the result, apply backpropagation, and print the training results.
If you take a detailed look at the code, you will notice that it is not very flexible in terms of reusability. It would be better if we divide the NeuralNet structure from the training part to be able to apply various learning algorithms on various neural net structures. Furthermore, if we want to experiment more with deep learning structures and various activation functions, we will have to change the data structures because for now, there is only one hidden layer defined. The backpropagation calculations have to be carefully tested in isolation in order to be sure we haven’t introduced any bugs. Once we are finished with all the refactoring, we will have to start to think about the performance of deep neural nets.
What I am trying to say is that if we have a real problem to solve, we need to take a look at the existing neural nets libraries. Implementing a neural net from scratch helps to understand the details of the paradigm, but one would have to put a lot of effort if a real-life solution has to be implemented from scratch. For this review, I have selected only pure Java neural net libraries. All of them are open-source, though Deeplearning4j is commercially supported. All of them are documented very well with lots of examples. Deeplearning4j has also CUDA support. A comprehensive list of deep learning software for various languages is available on Wikipedia, as well.
Examples using this library are also included in the GitHub repository with the XOR NeuralNet. It is obvious that there will be less code written using one of these libraries compared to the Java code needed for our example. Neuroph provides an API for datasets that allows for easier training data initialization, learning rules hierarchy, neural net serialization/persistence, and deserialization, and is equipped with a GUI. Encog is an advanced machine learning framework that supports a variety of advanced algorithms, as well as support classes to normalize and process data. However, its main strength lies in its neural network algorithms. Encog contains classes to create a wide variety of networks, as well as support classes to normalize and process data for these neural networks. Deeplearning4j is a very powerful library that supports several algorithms, including distributed parallel versions that integrate with Apache Hadoop and Spark. It is definitely the right choice for experienced developers and software architects. A XOR example is provided as part of the library packages.
Using one of the many libraries available, developers are encouraged to start experimenting with various parameters and make their neural nets learn. This article demonstrated a very simple example with a few neurons and backpropagation. However, many of the artificial neural networks in use today still stem from the early advances of the McCulloch-Pitts neuron and the Rosenblatt perceptron. It is important to understand the roots of the neurons as building blocks of modern deep neural nets and to experiment with the ready-to-use neurons, layers, activation functions, and learning algorithms in the libraries.
Opinions expressed by DZone contributors are their own.

Comments