Predictive Analysis Using Linear Regression With SAS

Linear regression is used to establish the relationship between a scalar dependent variable and one or more independent variables (explanatory variables). Linear regression consists of finding the best-fitted straight line through the points. This is known as a regression line. It is one of the most-used predictive technologies.

For example, if you want to predict the weight of person depending on their height, then the weight will be the dependent variable, as it needs to predict, and the height is the independent variable.

In SAS, PROC REG is used for linear regression to find the relationship between two variables.

Syntax

PROC REG DATA = dataset;
MODEL var1 = var2;

• dataset is the name of the dataset.

• var1 and var2 are the variables' names in the dataset used to find the correlation.

Here, you need to check for the P value and R-squared value.

• If the R-squared Value is greater than 0.7, then your model is good.

• If the P value is greater than 0.05, then the null hypothesis (h0) will be accepted. Otherwise, we will go for alternate hypothesis.

Simple Linear Regression

Modeling and establishing the relationship between one dependent variable and one independent variable is known as Simple Linear Regression.

y = β0 + β1x1 + ϵ

• x1 is the independent variable.

• y is the dependent variable.

• β0 is constant.

• β1 is the regression coefficient.

• ϵ is an error.

Data Person_Data ;
input weight height;
datalines;
30 130
40 140
45 145
50 160
55 170
60 172
;

proc reg data=work.person_data alpha=0.05 plots(only)=(diagnostics residuals observedbypredicted);;
model weight=height;
output out=WORK.Reg_stats p=p_ lcl=lcl_ ucl=ucl_ rstudent = r ;
run;
quit;

• weight is the dependent variable.

• height is the independent variable.

Output

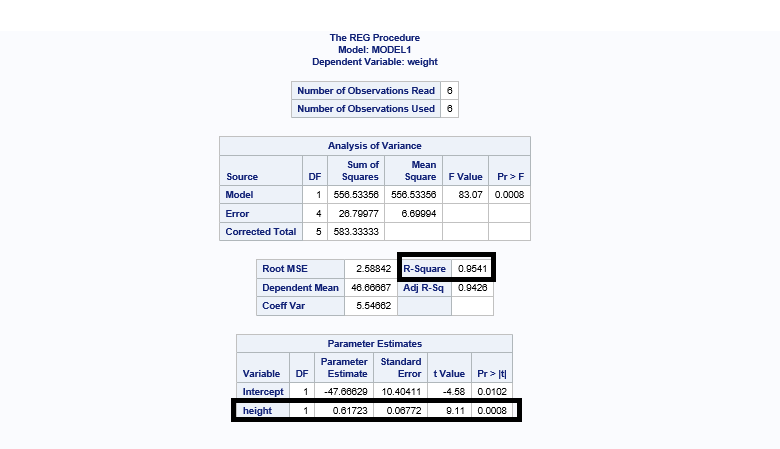
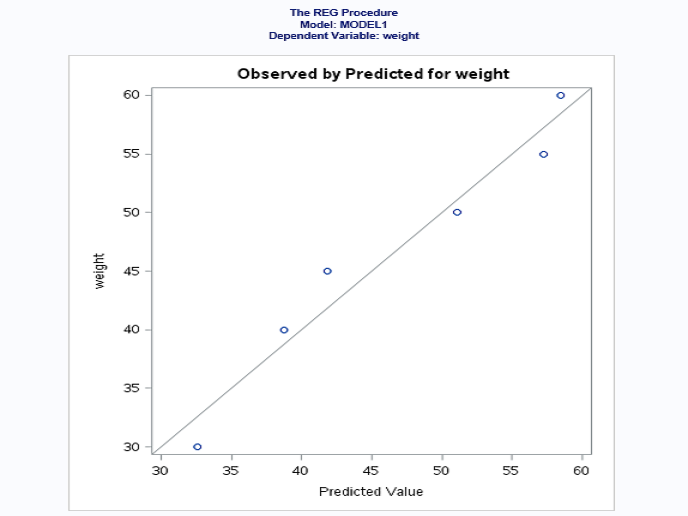
• R-squared value is 0.9541 (95.41%) > 0.7 (70%). This means that your model is a good fit.

• P value is 0.0008 < 0.05. This means that the height is a significant variable in your model.

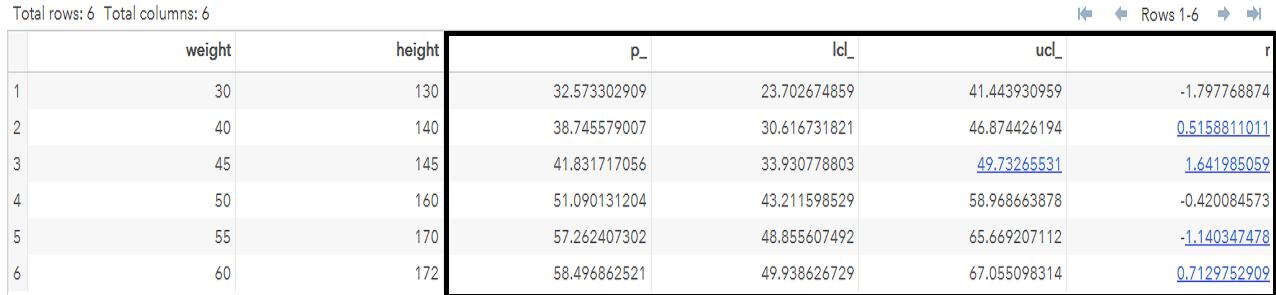
• The value of r is calculated to know if there are any outliers in any observations. If the value of r is greater than 2 and less than -2, then that observation has outliers. (Note: -2 < r < 2.)

In this case, there is no observation that falls under the outliers range. ucl is upper confidence limit and lcl is lower confidence limit.

Final Conclusion

The weight of the person is explained 95% by a significant variable (height).

Multiple Linear Regression

Modeling and establishing the relationship between one dependent variable and two or more independent variables is known as Multiple Linear Regression.

y = β0 + β1x1 + β2x2 + β3x3 + ϵ

x1, x2,and x3 are independent variables.

y is a dependent variable.

β0 is constant.

β1, β2, and β3 are regression coefficients.

ϵ is an error.

Data realstate_data ;
input sales_price no_of_bedroom no_of_flats no_of_garrage;
datalines;
300000 1 10 2
400000 1 10 3
600000 2 5 2
800000 3 3 2
1000000 4 3 2
;
proc reg data=work.realstate_data alpha=0.05 plots(only)=(diagnostics residuals observedbypredicted);;
model 'sales_price'n='no_of_bedroom'n 'no_of_flats'n 'no_of_garrage'n /;
output out=WORK.realstate_data_stats p=p_ lcl=lcl_ ucl=ucl_ rstudent = r ;
run;
quit;

• sales_price is the dependent variable.

• no_of_bedroom, no_of_flats, and no_of_garrage are independent variables.

Output

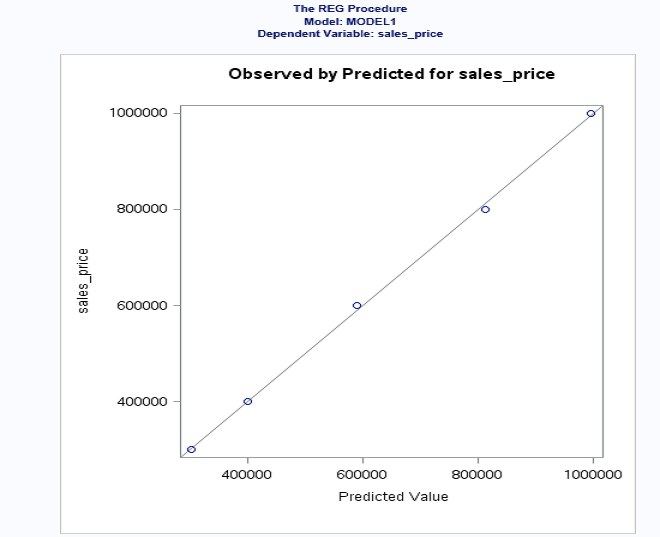
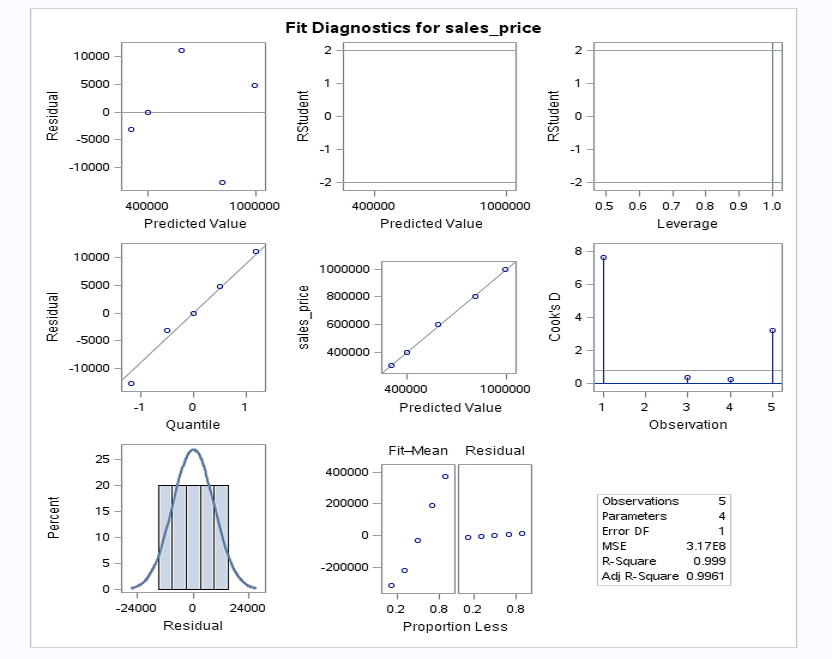
The value of R-squared is 0.9990 (99.99%)  > 0.7 (70%). This means that your model is a good fit.

The value of P for all independent variables is > 0.05, so there's no significant variable in your model.

I hope this article gives you understanding for implementing linear regression with SAS.