Solving a Clustering Problem Using the k-Means Algorithm With Oracle
Clustering algorithms let machines group data points or items into groups with similar characteristics. See how to use the k-means algorithm with Oracle to do clustering.
Join the DZone community and get the full member experience.
Join For FreeIn this article, I will solve a clustering problem with Oracle data mining.
Data science and machine learning are very popular today. But these subjects require extensive knowledge and application expertise. We can solve these problems with various products and software that have been developed by various companies. In Oracle, methods and algorithms for solving these problems are presented to users with the DBMS_DATA_MINING package.
With the DBMS_DATA_MINING package, we can create models such as clustering, classification, regression, anomaly detection, feature extraction, and association. We can interpret the efficiency with the models we create. The results we obtain from these models can be put into our business scenario.
The DBMS_DATA_MINING package does not come up by default on the Oracle database. For this reason, it's necessary to install this package first. You can set up your database Oracle Data Mining by following this link.
With the installation of the Oracle Data Mining package, three new dictionary tables are created:
SELECT * FROM ALL_MINING_MODELS;
SELECT * FROM ALL_MINING_MODEL_SETTINGS;
SELECT * FROM ALL_MINING_MODEL_ATTRIBUTES;The ALL_MINING_MODELS table contains information about all the models.

The ALL_MINING_MODELS_SETTINGS and ALL_MINING_MODELS_ATTRIBUTES tables contain parameters and specific details about these models.
Now, let's prepare an easily understood data set to solve a sample clustering problem.
CREATE TABLE KMEANSDATA
(
INSTANCE NUMBER,
X_AXIS NUMBER,
Y_AXIS NUMBER
);
INSERT INTO KMEANSDATA (INSTANCE, X_AXIS, Y_AXIS)
VALUES (1, 3, 5);
INSERT INTO KMEANSDATA (INSTANCE, X_AXIS, Y_AXIS)
VALUES (2, 2, 1);
INSERT INTO KMEANSDATA (INSTANCE, X_AXIS, Y_AXIS)
VALUES (3, 1, 1);
INSERT INTO KMEANSDATA (INSTANCE, X_AXIS, Y_AXIS)
VALUES (4, 4, 3);
INSERT INTO KMEANSDATA (INSTANCE, X_AXIS, Y_AXIS)
VALUES (5, 6, 1);
INSERT INTO KMEANSDATA (INSTANCE, X_AXIS, Y_AXIS)
VALUES (6, 7, 5);
INSERT INTO KMEANSDATA (INSTANCE, X_AXIS, Y_AXIS)
VALUES (7, 4, 4);
INSERT INTO KMEANSDATA (INSTANCE, X_AXIS, Y_AXIS)
VALUES (8, 5, 6);
INSERT INTO KMEANSDATA (INSTANCE, X_AXIS, Y_AXIS)
VALUES (9, 3, 8);
INSERT INTO KMEANSDATA (INSTANCE, X_AXIS, Y_AXIS)
VALUES (10, 5, 6);
COMMIT;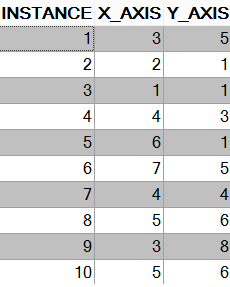
I created a simple dataset to understand the problem. My goal is to cluster the closest one in this data set with the k-Means algorithm.
k-Means is one of the simplest unsupervised learning algorithms. It solves the well-known clustering problem. It's a simple way to classify a given dataset through a certain number of clusters.
The following links provide detailed descriptions of the k-Means algorithm.
There are 10 records in the dataset. I want to collect these records in three different clusters, so I will choose a k value of 3. First, I look at the default parameter settings of my algorithm.
SELECT *
FROM TABLE (DBMS_DATA_MINING.GET_DEFAULT_SETTINGS)
WHERE setting_name LIKE 'KMNS%'OR setting_name like '%CLUS_NUM_CLUSTERS%';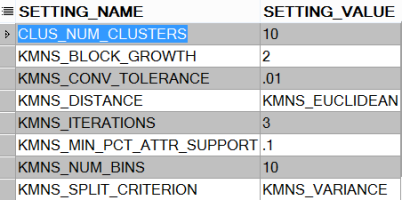 The default k parameter (
The default k parameter (CLUS_NUM_CLUSTERS) of the algorithm is set to 10, as seen in the default settings. I am creating a new table to set this to 3 to solve my problem and updating the relevant parameters.
CREATE TABLE kmeanssettings
AS
SELECT *
FROM TABLE (DBMS_DATA_MINING.GET_DEFAULT_SETTINGS)
WHERE setting_name LIKE 'KMNS%' OR setting_name like '%CLUS_NUM_CLUSTERS%';
UPDATE kmeanssettings
SET setting_value = 3
WHERE setting_name = 'CLUS_NUM_CLUSTERS';
UPDATE kmeanssettings
SET setting_value = 10
WHERE setting_name = 'KMNS_ITERATIONS';
COMMIT;
SELECT * FROM kmeanssettings; I have updated the relevant parameters as shown. Now, I will create my model using these settings:
I have updated the relevant parameters as shown. Now, I will create my model using these settings:
BEGIN
DBMS_DATA_MINING.CREATE_MODEL (
model_name => 'K_MEANNS_MODEL',
mining_function => DBMS_DATA_MINING.CLUSTERING,
data_table_name => 'KMEANSDATA',
case_id_column_name => 'INSTANCE',
target_column_name => NULL,
settings_table_name => 'KMEANSSETTINGS');
END;Our code runs and we have created our model according to the current settings. Now, let's take this model data set and examine the clustering results:
BEGIN
DBMS_DATA_MINING.APPLY (model_name => 'K_MEANNS_MODEL',
data_table_name => 'KMEANSDATA',
case_id_column_name => 'INSTANCE',
result_table_name => 'KMEANS_RESULT');
END;Now, let's examine the table:
SELECT * FROM KMEANS_RESULT;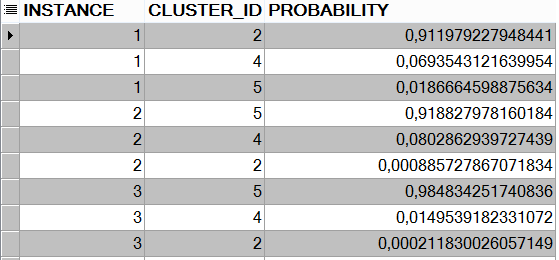
When we look at the result set, we see a total of 30 records. For this reason, we had 10 records in our total data set, and we gave the algorithm the number of clusters. In this case, the probability of each record separately for each set in the output of the algorithm is calculated (3X10 = 30). To see the exact result, find the maximum probability record of each element and list it.
SELECT t1.instance,
t1.CLUSTER_ID,
t1.probability,
t2.x_axis,
t2.y_axis
FROM (SELECT INSTANCE, CLUSTER_ID, PROBABILITY
FROM (SELECT T.*,
MAX (PROBABILITY)
OVER (PARTITION BY INSTANCE ORDER BY PROBABILITY DESC)
MAXP
FROM KMEANS_RESULT T)
WHERE MAXP = PROBABILITY) t1,
KMEANSDATA t2
WHERE t1.instance = t2.instance order by cluster_id;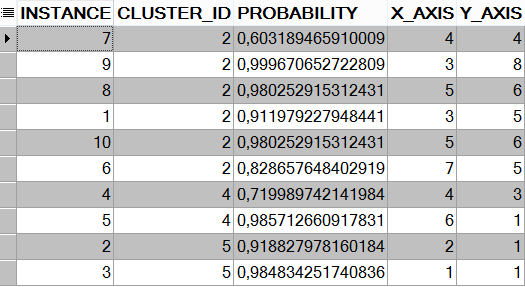 We see that our data set is distributed to three different clusters. Finally, let's look at the last situation on the chart.
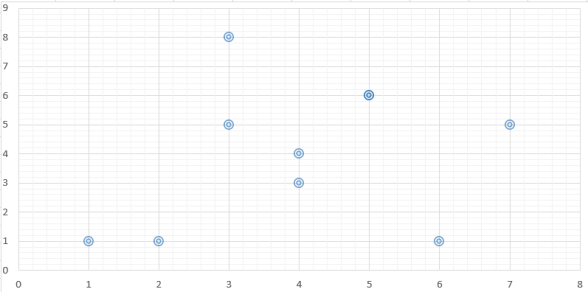
We see that our data set is distributed to three different clusters. Finally, let's look at the last situation on the chart.
 As can be understood from the graph, our model is logically clustered according to the k-Means algorithm.
As can be understood from the graph, our model is logically clustered according to the k-Means algorithm.
Opinions expressed by DZone contributors are their own.

Comments