Spotting Outliers With Isolation Forest Using sklearn

Isolation forest is an algorithm to detect outliers. It partitions the data using a set of trees and provides an anomaly score looking at how isolated the point is in the structure found. The anomaly score is then used to tell apart outliers from normal observations. In this post we will see an example of how IsolationForest behaves in simple case. First, we will generate one-dimensional data from bimodal distribution, then we will compare the anomaly score with the distribution of the data and highlighting the regions considered where the outliers fall.

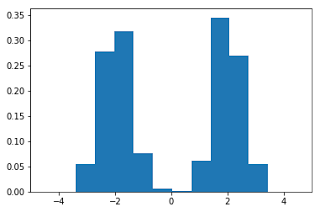
To start, let's generate the data and plot the histogram:

import numpy as np
import matplotlib.pyplot as plt

x = np.concatenate((np.random.normal(loc=-2, scale=.5,size=500), 
                    np.random.normal(loc=2, scale=.5, size=500)))

plt.hist(x, normed=True)
plt.xlim([-5, 5])
plt.show()

Here, we note that there are three regions where the data has low probability to appear: one on the right side of the distribution, another one on the left, and another around zero. Let's see if using IsolationForest we are able to identify these three regions:

from sklearn.ensemble import IsolationForest

isolation_forest = IsolationForest(n_estimators=100)
isolation_forest.fit(x.reshape(-1, 1))

xx = np.linspace(-6, 6, 100).reshape(-1,1)
anomaly_score = isolation_forest.decision_function(xx)
outlier = isolation_forest.predict(xx)

plt.plot(xx, anomaly_score, label='anomaly score')
plt.fill_between(xx.T[0], np.min(anomaly_score), np.max(anomaly_score), 
                 where=outlier==-1, color='r', 
                 alpha=.4, label='outlier region')
plt.legend()
plt.ylabel('anomaly score')
plt.xlabel('x')
plt.xlim([-5, 5])
plt.show()

In the snippet above, we have trained our IsolationForest using the data generated, computed the anomaly score for each observation, and classified each observation as an outlier or non-outlier. The chart shows the anomaly scores and the regions where the outliers are. As expected, the anomaly score reflects the shape of the underlying distribution and the outlier regions correspond to low probability areas.