Statistics for Rookies: Learn Data-Driven Decision-Making the Fun Way
Learn about the basics of inferential statistics and see what inferential statistics can do for you in terms of data-driven decision-making.
Join the DZone community and get the full member experience.
Join For FreeThis article is an excerpt from my forthcoming e-book, Statistics for Rookies: Learn Data-Driven Decision-Making the Fun Way.
Inferential Statistics: Sampling Techniques
Inferential statistics is the generalization of a sample population’s patterns and insights into the overall population. For us to understand this definition and cement the idea of inferential statistics in our minds, we need to understand the basics of inferential statistics:
Population (N)
Sample population (n)
Sampling techniques
Random sampling
Stratified sampling
Distributions
Before we start talking about these basics, though, it's a good idea to understand what inferential statistics can do for us.
Inferential statistics helps us move from a simple guess to an educated guess. By deploying various inferential statistical analyses and tests, we can either confirm whether what we guessed was right or wrong. These guesses can be termed as hypotheses, which we will cover later.
Definition of population:
Population is the collection of all individuals or items under consideration in a statistical study.
Definition of sample population:
The sample is the part of the population from which information is collected.
Population vs. Sample
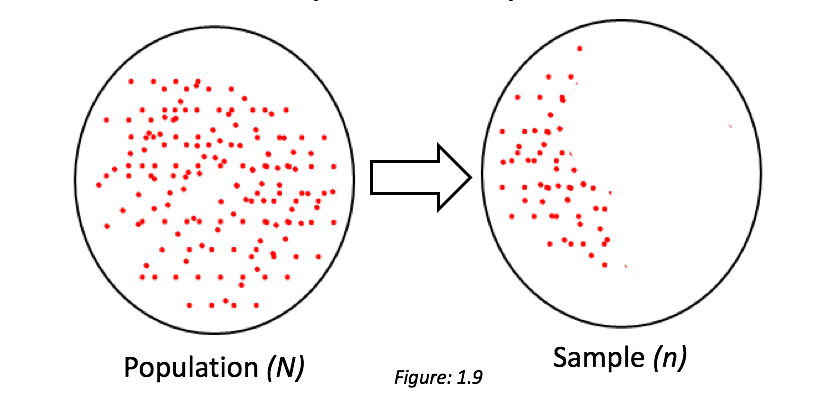
In statistics, we rely a lot on samples to draw inferences about the entire population. Inferential statistics provide a way to base our conclusions on the sample to the population by inferring the parameters of a population from data around the statistics of the sample. (Parameters can also be termed as μ "mean" and σ "standard deviation.")
I know this is getting a bit heavy, so let me put it this way: inferential statistics gives us a way to generalize the patterns observed on the overall population based on the inferential analyses and tests performed on the sample data.
This section can be considered the most important part of my book. We will develop the basic intuition of picking the most appropriate sample. It is also worth mentioning that it is very important for a researcher to work with samples rather working with the entire population.
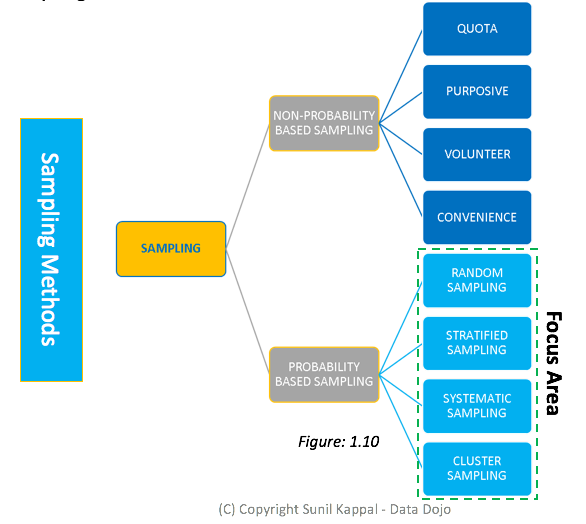
So, what are those sampling techniques?
There are a variety of sampling techniques available. However, as the theme of this book (statistics for rookies) suggests, I will discuss only two main sampling techniques: random sampling and stratified sampling. However, for the brainiacs who adore the intricacies of statistics, I have created a hierarchical view of various sampling methods:
The following table briefly describes various sampling methods with the associated pros and cons. Following that is an example based on survey data.

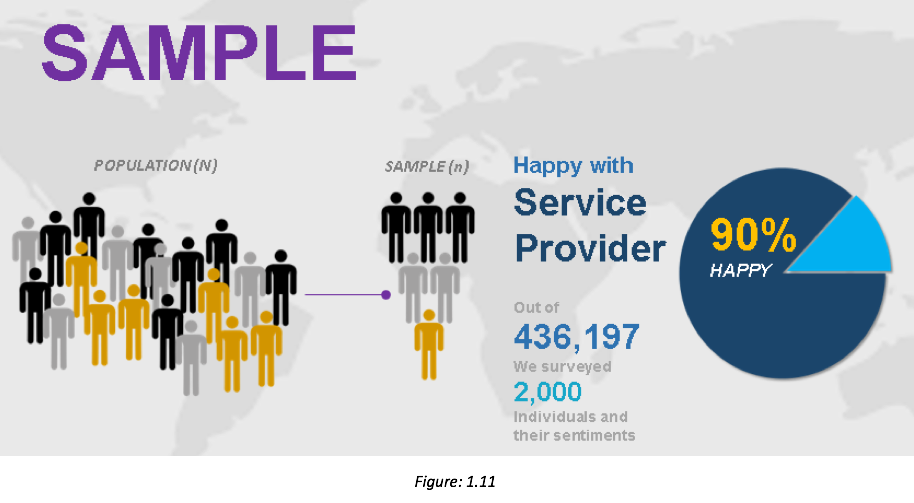
A survey was conducted with 2,000 people from the population of a particular state. In the above example, the “sample” is the 2,000 people surveyed from the state. This can be considered one example of sample size.
Random Sample
In a purely random sample, every unit of the population has an equal chance of being selected, removing bias from the selection procedure. To conduct a random sample, first, a population and a target sample size are defined. Units of the population are then chosen at random.
Because the selection is random, the sample is assumed to be representative of the population, and the information collected can be used to develop inferences about the whole population.
Caveat: Conducting a truly random sample may be challenging if the population is large, dispersed, or hidden.
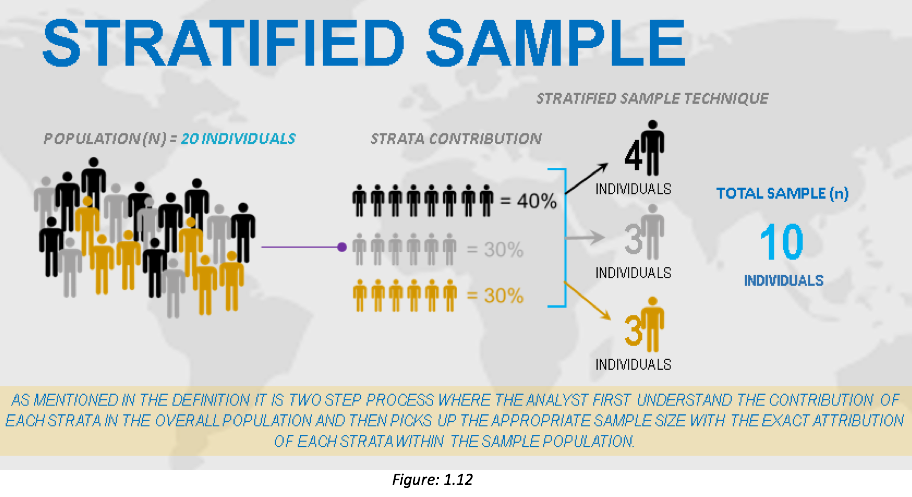
Stratified Sample
Stratified sampling is a random sampling method in which you divide members of a population into strata, or homogeneous subgroups. Stratified sampling is the process of selecting a sample that allows identified subgroups in the defined population to be represented in the same proportion that they exist in the population.
Steps to perform stratified sampling:
Identify and define the population.
Determine the desired sample size.
Identify the variables and subgroups (strata) for which you want to guarantee exact and equal representation.
Its advantages include that it provides a precise sample, that it can be used for both proportions and stratification sampling, and that the sample represents the desired strata.
Cluster Sampling
This can be defined as the process of randomly selecting intact groups, not individuals, within the defined population sharing similar characteristics. This can be also called multistage sampling.
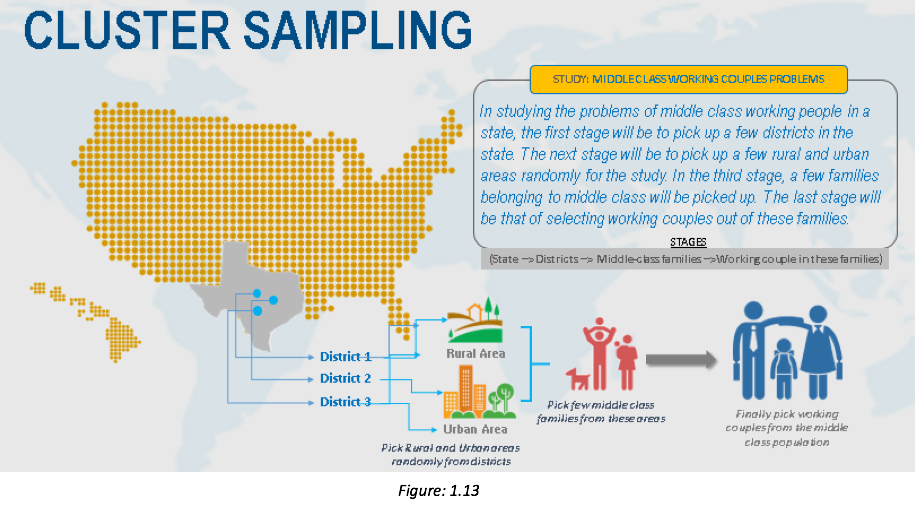
Steps to perform cluster sampling:
Identify and define the population.
Determine the desired sample size.
Identify and define a logical cluster.
List all clusters that make up the population.
Estimate the average number of population members per cluster.
Determine the number of clusters needed by dividing the sample size by the estimated size of a cluster.
Randomly select the needed number of clusters by using a table of random numbers.
Include in your study all population members in each selected cluster.
Its advantages include that it is efficient, that you don’t need excessive details about the population members, and that it is very useful for educational research.
Systematic Sampling
Systematic sampling is the process of selecting individuals within the defined population from a list by taking every Nth name.
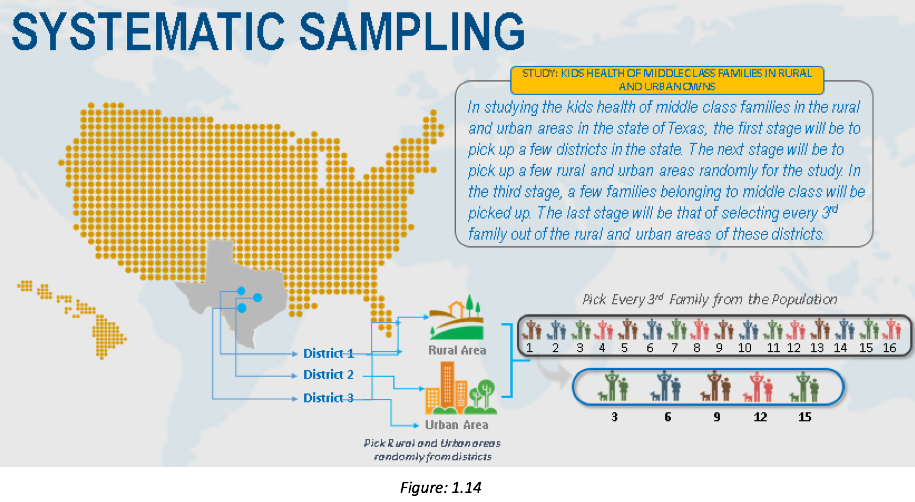
Steps to perform systematic sampling:
Identify and define the population.
Determine the desired sample size.
Obtain a list of the population.
Determine what N is equal to by dividing the size of the population by the desired sample size.
Start at some random place in the population list. Close your eyes and point your finger to a name!
Starting at that point, take every Nth name on the list until the desired sample size is reached.
If you reach the end of the list before you reach the desired sample, go back to the top of the list.
Its main advantage is that the sample selection process is simple.
Conclusion
To conclude, the process of selecting a number of individuals for a study in such a way that the individuals represent the larger group from which they were selected is called sampling. The group of individuals selected for a study whose characteristics exemplify the larger group from which they are selected is called a sample. The larger group from which individuals are selected to participate in a study is called a population.

Stay tuned for more details on the full release of this e-book!
Opinions expressed by DZone contributors are their own.

Comments