The Developer's Guide to Collections: Sets
Time for another deep dive into Java collections! This time, we focus on the concept of sets, the set interface, and everything you can do with sets.
Join the DZone community and get the full member experience.
Join For FreeThe set is one of the most mathematical abstractions in the Java Collections Framework (JCF) and plays an integral role in numerous use cases, including status or state flags, unique collections, and ordered groups of unique elements. In order to support these various goals, the Set interface and its implementation classes include semantics that closely mirror the concepts and characteristics of set theory developed by Georg Cantor.
In this continuation of The Developer's Guide to Collections series, we explore the Set interface and its associated implementations, paying special attention to the mathematical underpinnings that the interface mimics. We also take a look at the hierarchy that turns the Set interface into workable and usable implementation classes. Lastly, we compare the advantages and disadvantages of each of the implementation classes and under what conditions each is best suited. In order to start this deep-dive, we must start with the most simple, yet fundamental aspect of sets in the JCF: Set theory.
The Concept of a Set
The concept of a set was first formalized by German Mathematician Georg Cantor in the late 1800s and is often called set theory. In mathematics, a set is a collection of unique elements, denoted by curly braces, such as A = {1, 2, 4}. If some value, a, is contained in the set A, a is considered an element or member of set A and is denoted with the symbols a ∈ A. In some cases, membership of a set is more informally referred to as an in relationship (i.e. a is in A). A set that contains no elements is called the empty set or null set and is denoted as {} or the symbol ∅ (i.e. an empty set, A, is A = {} or A = ∅). More formally, an empty set is a set, A, with a cardinality of zero: |A| = 0.
One set, A, is considered a subset of another set, B, if all elements of A are contained in B, as denoted by A ⊆ B. For example, A = {1, 2} is a subset of B = {1, 2, 3, 4}. If one subset, A, has all of its elements contained in B and is not equal to B (i.e. A ⊆ B and A ≠ B), it is considered a proper subset, as denoted by A ⊂ B. For example, A = {1, 2} is a proper subset of B = {1, 2, 3, 4} (i.e. A ⊂ B), but C = {1, 2, 3, 4} is not a proper subset of B (i.e. C ⊄ B), although C is a subset of B (i.e. C ⊆ B since C = B).
Sets also have a series of associated binary operations that add or remove elements from a set. The first of these operations is the union of two sets A and B, denoted by A ∪ B, which results in the combination of elements of A and B. For example, if A = {1, 3, 4} and B = {1, 2, 5, 7}, then A ∪ B = {1, 2, 3, 4, 5, 7}. Note that since the elements of a set are distinct, the element 1 is only included once. The intersection of two sets A and B, denoted by A ∩ B, results in the elements that are common between A and B. For example, if A = {1, 2, 3, 4} and B = {2, 4, 5}, A ∩ B = {2, 4}. Lastly, the difference between two sets A and B (sometimes formally referred to as the asymmetric difference), as denoted by A \ B, is the set of all members of A that are not members of B. For example, if A = {1, 2, 3, 4} and B = {2, 4, 5}, then A \ B = {1, 3}. These basic binary operations are best visually illustrated below using Venn diagrams.
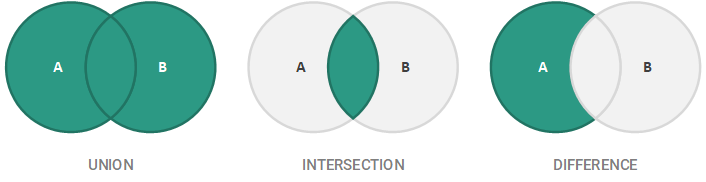
In summary, we have the following characteristics and operations for sets:
- Set: A collection of unique values
- Element: A value contained in a set
- Null or empty set: A set of zero elements (a set with a cardinality of zero)
- Subset: A set whose elements are contained in another set
- Proper subset: A set that is a subset of another set but not equal
- Union: The combined elements of two sets
- Intersection: The elements common between two sets
- Difference: The elements contained in one set but not contained in another
In the following section, we will translate these mathematical principles into the Set interface and explore the features common between the formal definition of a set and the Java Set interface.
The Set Interface
The striking part of the Set interface in Java Development Kit (JDK) 9 is that it does not introduce any new methods not found in the Collection interface. The only differences between a Set and Collection are found in the semantics of the mutation methods. The JDK 9 Set interface is listed in the snippet below:
public interface Set<E> extends Collection<E> {
int size();
boolean isEmpty();
boolean contains(Object o);
Iterator<E> iterator();
Object[] toArray();
<T> T[] toArray(T[] a);
boolean add(E e);
boolean remove(Object o);
boolean containsAll(Collection<?> c);
boolean addAll(Collection<? extends E> c);
boolean retainAll(Collection<?> c);
boolean removeAll(Collection<?> c);
void clear();
boolean equals(Object o);
int hashCode();
default Spliterator<E> spliterator() { /* ... */ }
}The only method whose default implementation is redefined in the Set interface is the spliterator. As we saw previous in the List interface, this redefinition of the spliterator method is done in order to optimize the returned Spliterator for Set operations, rather than general-purpose collections. We will explore this default implementation in more detail in the following sections.
The main differences in the Set and Collection interfaces are found in the semantics of the mutation methods, such as add, addAll, removeAll, and retainAll. In standard collections, these methods simply add, remove, and retain elements in a collection, respectively. In a Set, these operations correspond to the binary set characteristics and operations described in the mathematical set concept. For example, adding an element into a Set that already exists does not change the set (the addition is not performed) since sets may only contain unique values.
Additionally, an addAll acts as a union of the set with the provided collection (preserving unique values); removeAll acts a difference of the set with the provided collection; and retainAll acts as an intersection of the set with the provided collections. Likewise, the constructors of the Set class also ensure that the elements of the supplied Collection are added only if there does not exist a duplicate value already present in the Set.
add(E e)
This optional operation–one that is not required by an implementation and may throw an UnsupportedOperationException if the implementation does not support it–adds an element to the Set if a duplicate element is not already contained in the Set and returns true if the Set was altered (i.e. if the addition was successful). A duplicate element of element a is defined as any element, b, such that a.equals(b) returns true. If a duplicate of the supplied element exists in the Set, no addition is performed and the add method returns false.
addAll(Collection c)
This optional operation adds all of the elements of the supplied collection to the Set, ensuring that no duplicate values are added, and returns true if the Set was altered. If the supplied collection is a Set, this method effectively results in a union of the two sets. This union is illustrated in the figure below.

removeAll(Collection c)
This optional operation removes all of the elements present in the supplied collection from the Set, returning true if the Set was altered. If the supplied collection is a Set, this method effectively results in the asymmetric difference of the two Sets. This symmetric difference is illustrated in the figure below.
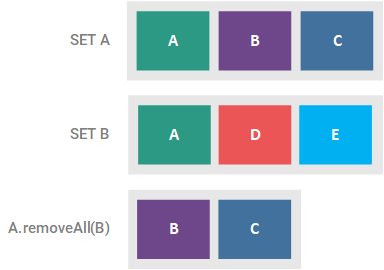
retainAll(Collection c)
This optional operation retains only the elements present in the supplied Set, returning true if the Set is altered. If the supplied collection is a Set, this method effectively results in the intersection of the two sets. This intersection is illustrated in the figure below.

spliterator
Just as with many of the other Collection types, the Set interface overrides the spliterator method in order to return a Spliterator more suited to the characteristics of the Set type. In the case of Set, its Spliterator has the required characteristics that each element in the Spliterator be distinct, as depicted in the following JDK 9 default implementation for the Set#spliterator method:
@Override
default Spliterator<E> spliterator() {
return Spliterators.spliterator(this, Spliterator.DISTINCT);
}Spliterators are an involved topic and beyond the scope of this series. For more information, see the official Spliterator documentation.
equals & hashCode
The equals method of a Set is based on an element-by-element equality of two sets. Therefore, in order for an object to be equal to a Set, it must be a Set object or one that extends Set, must have the same number of elements as the Set, and each of its elements must match the elements of the Set. In a likewise fashion, the hash code for a Set is the sum of the hash codes of its elements, resulting in a hash code that the hash codes of two Sets, a and b, are equal so long as the two sets are equal (i.e. a.equals(b)).
Summary
In general, any method that adds an element to a Set ensures that no duplicates are added and that at any given time, all elements of a Set are unique. This amounts to a class invariant and is never disobeyed for the life of the Set. When supplied Set objects, the methods that operate on collections perform the binary set operations as follows:
- Union:
addAll - Intersection:
retainAll - Asymmetric difference:
removeAll
In general, the specification for the Set class closely mimics that characteristics and operations for a mathematical set, while still implementing the standard Collection interface.
The Set Hierarchy
Based on a foundational understanding of the mathematical concepts behind a set and our understanding of how the Set interface incorporates these concepts, we can now explore the class hierarchy for the Set interface. The JDK 9 Set hierarchy is illustrated in the figure below, where green boxes represent interfaces, blue boxes represent abstract classes, and purple boxes represent concrete implementation classes.
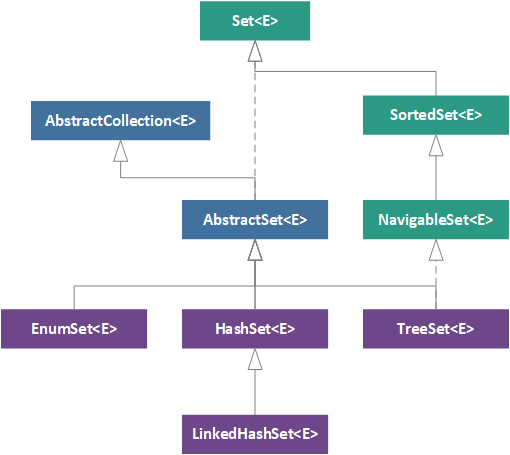
As covered in The Developer's Guide to Collections, the root of the Set hierarchy is the Set interface, followed by the AbstractSet abstract class (which in turn extends the AbstractCollection abstract class). From this abstract class, three concrete implementations are derived: (1) EnumSet, (2), HashSet, and (3) LinkedHashSet. Apart from these direct ancestors of the Set interface, there are also two other interfaces included in the hierarchy: (1) SortedSet and (2) NavigableSet. The last concrete implementation class, TreeSet, implements the NavigableSet interface, which in turn implements the SortedSet interface.
SortedSet
The SortedSet interface provides a total ordering of the elements, where each element is ordered relative to the other elements in the Set. This order is accomplished either through use of an explicit Comparator object or through natural ordering (if each element implements the Comparable interface). In order to support this ordering, the Iterator returned by classes that implement SortedSet will traverse the Set in ascending order, based on its stated order (i.e. either explicit Comparator ordering or its natural ordering). This interface also provides the following methods that allow for ordered access of the elements in the SortedSet:
first: Returns the first (lowest) element in theSetlast: Returns the last (highest) element in theSetsubSet(E fromElement, E toElement): Returns a newSetcontaining the elements from thefromElement, inclusive, to thetoElement, exclusiveheadSet(E toElement): Returns a newSetcontaining the elements from the head of theSet, inclusive, to thetoElement, exclusivetailSet(E fromElement): Returns a newSetcontaining the elements from thefromElement, inclusive, to the tail of theSet
NavigableSet
The NavigableSet expands on this definition by providing methods that allow for clients to obtain the closest target to some search criteria. This interface provides the following methods to support this search-based access to a Set:
lower(E element): Returns greatest element less than the supplied elementhigher(E element): Returns least element greater than the supplied elementfloor(E element): Returns the greatest element less than or equal to the supplied elementceiling(E element): Returns the least element greater than or equal to the supplied element
For all of these methods, if no element can be found matching the desired criteria, null is returned. With an understanding of the hierarchical structure that makes up the sets in Java, we can now look at some of the concrete implementation classes, along with their relative advantages and disadvantages, in greater detail.
EnumSet
The EnumSet class is a special purpose Set designed to support enumerations (enums). In many applications, there exists a need for some means of compactly representing flag values associated with some state. For example, if we create a typography or word processing application, we may want flags to denote if a specific set of text is bolded, underlined, or italicized. In many native applications (such as those written in C or C++), bit fields are used, where each desired flag is given a successive bit value (e.g. 0x01, 0x02, 0x04, etc.) and bitwise operations are used to set flags and masks are used to discover if certain flags are set.
While these types of flags are highly efficient, they are cumbersome and prone to errors. As an alternative, Java provides the EnumSet, which is created based on some number of enum constant values (which may include none or all) from an enum class and represents them as a bit vector. This internal representation is highly efficient and very compact, providing a high enough performance advantage to be suited for most flag-based use cases. An example of a possible use for the EnumSet is depicted in the listing below.
public interface Style {
public String apply(String text);
}
public enum BasicStyle implements Style {
BOLD {
public String apply(String text) { return "<strong>" + text + "</strong>"; }
},
UNDERLINE {
public String apply(String text) { return "<u>" + text + "</u>"; }
},
ITALIC {
public String apply(String text) { return "<em>" + text + "</em>"; }
};
}
public class HtmlFormatter {
public String format(String text, Set<? extends Style> styles) {
String formattedText = text;
for (Style style: styles) {
formattedText = style.apply(formattedText);
}
return formattedText;
}
}
HtmlFormatter formatter = new HtmlFormatter();
String text = formatter.format("Hello, world!", EnumSet.of(BasicStyle.BOLD, BasicStyle.ITALIC));
System.out.println(text); // Output: <em><strong>Hello, world!</strong></em>For the sake of comparison, we could implement the same logic in a similar manner using bit fields and bitwise comparison operations:
public interface Styles {
public static final int BOLD = 0x01;
public static final int UNDERLINE = 0x02;
public static final int ITALIC = 0x04;
}
public class HtmlFormatter {
public String format(String text, int styles) {
String formattedText = text;
if ((styles & Styles.BOLD) == Styles.BOLD) {
formattedText = "<strong>" + formattedText + "</strong>";
}
if ((styles & Styles.UNDERLINE) == Styles.UNDERLINE) {
formattedText = "<u>" + formattedText + "</u>";
}
if ((styles & Styles.ITALIC) == Styles.ITALIC) {
formattedText = "<em>" + formattedText + "</em>";
}
return formattedText;
}
}
HtmlFormatter formatter = new HtmlFormatter();
String text = formatter.format("Hello, world!", Styles.BOLD | Styles.UNDERLINE);
System.out.println(text);Although the bit field alternative may appear more compact, it is much less precise in its language. For example, we can provide any integer value as a style, not just enumerated styles (or an object that implements the Style interface). Additionally, the use of enums and the EnumSet allows for encapsulation of formatting logic and iteration over any number of styles, respectively. In the case of bit fields, we must check to see if each of the possible style values has been provided and format the supplied string accordingly.
HashSet
A HashSet is simply a Set backed by a HashMap and permits null values while making no guarantees about the order of the elements in the Set. In general, the add, remove, contains, and size methods are executed in constant time (assuming a properly constructed hashCode method for the objects that represent its elements). In the case of iteration, the HashSet class is linear with respect to the sum of the number of elements and the number of buckets (or capacity). In order to tune a HashMap object, two options are provided:
- Initial capacity: The capacity of the
Setupon creation - Load factor: The ratio of elements to the capacity of the
HashSetbefore the capacity is automatically increased (see the HashMap documentation for more information)
In general, if the ordering of elements is not needed, the HashSet class provides the best overall performance and should be considered the default Set implementation used for unordered sets.
TreeSet
The TreeSet provides total ordering of its elements through either an explicit Comparator object or through natural ordering. Internally, this implementation is backed by a TreeMap which allows for elements to be ordered upon creation and iterated in order using its Iterator implementation. In general, this class provides log(n) performance for its add, remove, and contains methods and should be used when ordering of elements is required. In most other cases, a HashSet should be used. It should also be noted that this Set implementation rejects null values if natural ordering is used or if the explicitly supplied Comparator object does not support nulls.
LinkedHashSet
The LinkedHashSet is a compromise between the unordered HashSet and totally ordered TreeSet. This Set implementation is backed by a linked list and ensures that its elements are iterated in order of insertion, with the most recent addition occupying the last location in the set. For example, if some element A was added to the set and then some element B was added, iterating through this set would result in A followed by B.
These insertion-ordered characteristics are important for clients that require that a Set implementation deterministically iterates over its elements. In general, the execution performance of add, remove, and contains is nearly that of a HashSet. Additionally, this Set implementation supports all optional operations and allows for null values to be added (at most one null value).
Comparison
The following table provides some general guidelines that aid in deciding which Set implementations are best for certain scenarios and for understanding the performance trade-offs between these different implementations. For more information on the advantages and disadvantages of each Set implementation, see this Set Implementation Oracle article.
| Set | Description |
EnumSet |
Primarily used as an alternative to bit fields. This set should be used whenever a series of enum constants should be grouped together in a collection, such as iteration over a set of flags. |
HashSet |
A generally well-performing Set implementation backed by a HashMap. This implementation allows for its initial capacity and load factor to be tuned upon creation and should be the default implementation used when the ordering of the elements in a set is not required. |
TreeSet |
An ordered set that ensures that its elements are ordered according to an explicit Comparator object or by natural ordering (depending on the constructor used) and exhibits a log(n) efficiency when executing its add, remove, and contains methods. This implementation should only be used when total ordering is needed for its elements and a HashSet should be used instead is total ordering is not required. |
LinkedHashSet |
A compromise between the efficiency of the HashSet and the total ordering of the TreeSet: This implementation provides insertion ordering with performance nearly identical to that of the HashSet. This implementation should be used when consistent and deterministic ordering of iteration is needed (rather than total ordering). If consistent ordering is unneeded, a HashSet should be used instead. |
Conclusion
Sets are one of the more mathematical aspects of the JCF and have a number of very important use cases, including flag values (as formerly represented by bit fields) and as collections of unique elements. Although the mathematical characteristics of sets may seem orthogonal to the standard Collection interface methods, the JCF succinctly incorporates these formal concepts with its existing methods, resulting in a Set interface that does not add any additional methods to those inherited from the Collection interface. Its implementations also provide a useful array of features, including encapsulation of enum constants, constant-time performance, and ordering of elements. While sets are not the most widely used of the collection types, they play an important role in many precise use cases and should be in the toolbox of any experienced Java developer.
If you enjoyed this article and want to learn more about Java Collections, check out this collection of tutorials and articles on all things Java Collections.
Opinions expressed by DZone contributors are their own.

Comments