Using a Chi-Square Test to Satisfy Benford's Law With Python

here's a fun quick excursion using a very short python program that illuminates the somewhat counterintuitive basis for benford's law. quick, interesting and refreshing. we're all geeks here right?

a while back i wrote about how the leading digits of factorials follow benford’s law . that is, if you look at just the first digit of a sequence of factorials, they are not evenly distributed. instead, 1’s are most popular, then 2’s, etc. specifically, the proportion of factorials starting with n is roughly log ₁₀ (1 + 1/ n ).

someone has proved that the limiting distribution of leading digits of factorials exactly satisfies benford’s law . but if we didn’t know this, we might use a chi-square statistic to measure how well the empirical results match expectations. as i argued in the previous post , statistical tests don’t apply here, but they can be useful anyway in giving us a way to measure the size of the deviations from theory.

benford’s law makes a better illustration of the chi-square test than the example of prime remainders because the bins are unevenly sized, which they’re allowed to be in general. in the prime remainder post, they were all the same size.

the original post on leading digits of factorial explains why we compute the leading digits the way we do. only one detail has changed: the original post used python 2 and this one uses python 3. integer division was the default in python 2, but now in python 3 we have to use // to explicitly ask for integer division, floating point division being the new default.

here’s a plot of the distribution of the leading digits for the first 500 factorials.

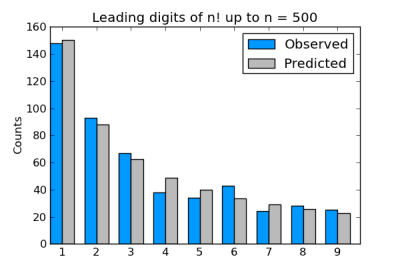
and here’s code to compute the chi-square statistic:

    from math import factorial, log10

    def leading_digit_int(n):
        while n > 9:
            n = n//10
        return n

    def chisq_stat(o, e):
        return sum( [(o - e)**2/e for (o, e) in zip(o, e)] )

    # waste the 0th slot to make the code simpler.
    digits = [0]*10

    n = 500
    for i in range(n):
        digits[ leading_digit_int( factorial(i) ) ] += 1

    expected = [ n*log10(1 + 1/n) for n in range(1, 10) ]

    print( chisq_stat(digits[1:], expected) )

this gives a chi-square statistic of 7.693, very near the mean value of 8 for a chi-square distribution with eight degrees of freedom. (there are eight degrees of freedom, not nine, because if we know how many factorials start with the digits 1 through 8, we know how many start with 9.)

so the chi-square statistic suggests that the deviation from benford’s law is just what we’d expect from random data following benford’s law. and as we said before, this suggestion turns out to be correct.