Random Forest as a Classifier: A Spark-based Solution
In this article, the author will demonstrate how to use the Random Forest as a classifier and regressor with Big Data processing engine Apache Spark.
Join the DZone community and get the full member experience.
Join For FreeIn this article, I will demonstrate how to use Random Forest (RF) algorithm as a classifier and a regressor with Spark 2.0. The first part of this article will cover how to use the RF as a classifier; while the second part will focus on how to use the same algorithm as a regressor on real datasets.
Random Forest as a Classifier
Random forest [1, 2] (also sometimes called random decision forest [3]) (RDF) is an ensemble learning technique used for solving supervised learning tasks such as classification and regression. An advantageous feature of RF is that it can overcome the overfitting [4] problem across its training dataset.
A forest in the RF or RDF usually consists of hundreds of thousands of trees. These trees are actually trained on different parts of the same training set [1-3]. More technically, an individual tree that is grown very deep tends to learn from the highly unpredictable patterns. This kind of nature of the trees creates overfitting problems on the training sets. Moreover, low biases make the classifier a low performer even if your dataset quality is good in terms of feature presented [1].
On the other hand, an RF helps to average multiple decision trees together with the goal of reducing the variance to ensure consistency by computing proximities between pairs of cases. However, this increases a small bias or some loss of the interpretability of the results. But eventually, the performance of the final model increased dramatically.
Main Advantages of Using Random Forest Algorithm
As discussed in literature [1, 2, 5] following are the main advantages of using an RF algorithm:
- RF provides excellent accuracy among current classification and regression algorithms
- It can be applied efficiently to large-scale datasets for both classifications as well as regressions analysis making it scalable based on increasing data size. Consequently, it's a perfect algorithm for making predictive analytics on Big Data.
- It can handle thousands of input features and variables at a time. That means high dimensional dataset can be handled and used to make predictive analytics using the RF model efficiently.
- It provides dimensionality reduction facility without deleting unwanted variables from the training dataset. As a result, it gives an estimate of what variables are important and should be considered during model building for the classification
- It has an effective technique embedded for estimating missing or null values. Therefore, it can maintain the accuracy level (i.e., stable performance) even when a large proportion of the dataset are missing [1]. This also implies that it is resilient against the null values
- Generated forests and trained model can be saved for future use that can be applied to other datasets later stages. This way it provides model adaptability for new data types
- It can compute proximities between pairs of cases which provide interesting views on the data. These views help in clustering and locating the outliers after scaling the data eventually
- The above capabilities also can be extended to unlabelled data. That means that RF can also be applied to unsupervised learning problems like clustering, high-level data views generation, and outlier detection
- Even a supervised RF algorithm can be applied to solve unsupervised learning problem. For example anomaly detection from large scale categorical dataset presented at [17]. These advantages make the RF as a suitable algorithm for enabling incremental learning
- Above all, as usually RF algorithm does not overfit, so you can run and build the model by specifying as many trees as you want.
For more on pros and cons of the RF algorithm, readers can refer the book titled "Large Scale Machine Learning with Spark" published recently with the latest machine learning algorithms with Spark 2.0.0 release [10].
How Does It Work?
Particularly, general techniques like bootstrap aggregating and bagging are applied to the trees that are generated while building the forests in RF [1, 2, 5]. This is the typical first step in the RF algorithm also called begging to RF. As already mentioned that typically hundreds to thousands of trees are constructed dynamically (of course based on the parameter setting). Moreover, the number of trees depends on:
- The size and nature of the training set
- Model building parameters like a number of classes, a number of beans and number of maximum depth etc.
Nevertheless, finding the optimal number of trees is a matter of hyperparameter tuning a part of tuning machine learning model. Therefore, optimal numbers of trees say N can be found by performing hyperparameter tuning using cross-validation and train split of the dataset. Alternatively, it can be found by observing the out-of-bag error [6, 7] which is often expressed using in terms of training and test error [1, 2].
After that proximities [8] are computed for each pair of cases when all the trees are built using the complete dataset (unless you randomly split the data into training and test set). Furthermore, "when two cases occupy the same terminal node, proximity is increased by one for each case" [1]. However, at the end of the each iteration, proximity values are normalized by dividing them by the number of trees (that were built and specified during the training period) [1].
You might be wondering why the proximity calculation is so important! The reality is that the proximity calculation has many contributions towards making the prediction better. For example, for replacing missing data, null values and locating the outliers from a set of the cluster. Finally, it also helps produce low-dimensional views of the data [1, 5, 6].
On the one hand, for a classification problem with say n features, the value of n is usually rounded down as √n. That means, only √nfeatures are used in each split on the training set. On the other hand, for a regression analysis problem using RF, the inventors (i.e., Leo Breiman and Adele Cutler et al.) recommend using the rounded value as n/3 with a minimum tree node size of 5 as the default [9].
How Did Spark Implement the RF Algorithm?
Spark has implemented and represented two classes that implement two learning algorithms for classification and regression that both support using both continuous and categorical features. The settings for featureSubsetStrategy are based on the following references [15, 16]. The configuration parameters for the random forest algorithm are:
- Type of random forest (classification or regression),
- Feature type (continuous, categorical),
- The depth of the tree and quantile calculation strategy etc.
While using the RF as a classifier, here goes the parameter setting:
- If the number of trees is 1, then no bootstrapping is used at all; however, if the number of trees is > 1, then the bootstrapping is accomplished. Where, the parameter featureSubsetStrategy signifies the number of features to be considered for splits at each node. The supported values are "auto", "all", "sqrt", "log2", "onethird"
- The supported numerical values are (0.0-1.0] and [1-n]. However, if featureSubsetStrategy is chosen as "auto", the algorithm chooses the best feature subset strategy automatically
- If the numTrees == 1, the featureSubsetStrategy is set to be "all". However, if the numTrees > 1 (i.e., forest), featureSubsetStrategy is set to be "sqrt" for classification ("onethird" for regression)
- Moreover, if a real value "n" is in the range (0, 1.0] is set, n*number_of_features is used consequently. However, if an integer value "n" is in the range (1, the number of features) is set, only n features are used alternatively
- The parameter categoricalFeaturesInfo which is a map is used for storing arbitrary of categorical features. An entry (n -> k) indicates that feature n is categorical with k categories indexed from 0: {0, 1,...,k-1}
- The impurity criterion used for information gain calculation. The supported values are “gini” and “variance”. The former is the only supported value for classification. The latter is used for regression
- The maxDepth is the maximum depth of the tree. (e.g., depth 0 means 1 leaf node, depth 1 means 1 internal node + 2 leaf nodes). However, the suggested value is 4 to get a better result
- The maxBins signifies the maximum number of bins used for splitting the features; where the suggested value is 100 to get better results
- Finally, the random seed is used for bootstrapping and choosing feature subsets to avoid the random nature of the results.
As already mentioned, since RF is fast and scalable enough for the large-scale dataset, Spark is a suitable technology to implement the RF to take the massive scalability. However, if the proximities are calculated, storage requirements also grow exponentially.
The next section shows a step-by-step example of using the RF as a classifier with Spark 2.0. For the demonstration purpose, Spark 2.0.0 will be used. The application that I will be showing is written in Java as Maven project on Eclipse.
Optical Character Prediction with Spark MLlib
Image processing or computer vision which is two classical but still are emerging research areas that often make the proper utilization of many types of machine learning algorithms. There are several use cases where the relationships of linking the patterns of image pixels to higher concepts are extremely complex and hard to define and of course computationally extensive too [10].
From the practical point of view, it's relatively easier for a human being to recognize if an object is a face, a dog, or letters or characters. However, defining these patterns under certain considerations is difficult. Additionally, image related datasets are often noisy. In this section, we will develop a model similar to those used at the core of the Optical Character Recognition (OCR) used as the document scanners. This kind of software help to process paper-based documents by converting printed or handwritten text into an electronic form to be saved in a database.
Data Collection
When an OCR software first processes a document, it divides the paper or any object into a matrix such that each cell in the grid contains a single glyph (also known different graphical shapes), which is just an elaborate way of referring to a letter, symbol, or number or any contextual information from the paper or the object.
To demonstrate the OCR pipeline, let's assume that the document contains only alpha characters in English that matching glyphs to one of the 26 letters: A to Z. We will use the OCR letter dataset from the UCI Machine Learning Data Repository [11]. The dataset was denoted by W. Frey and D. J. Slate et al. While exploring the dataset, I have found that the dataset contains 20,000 examples of 26 English alphabet capital letters as printed using 20 different randomly reshaped and distorted black and white fonts as glyph of different shapes. Therefore, predicting a character or an alphabet from 26 alphabets make this problem a multiclass classification problem having 26 classes.

Figure 1: some of the printed glyphs [courtesy of the article titled Letter recognition using Holland-style adaptive classifiers, ML, V. 6, p. 161-182, by W. Frey and D.J. Slate (1991)].
For more information about the dataset, refer to Letter recognition using Holland-style adaptive classifiers [12]. Figure 1 shows the images that I explained above. It was published by Frey and Slate et al., provides an example of some of the printed glyphs. Distorted in this way, therefore, the letters are computationally challenging for a computer to identify, yet are easily recognized by a human being. Figure 2 shows the statistical attributes of top 20 rows.
Exploration and Preparation of the Dataset
According to the documentation provided by Frey and Slate et al. [11] when the glyphs are scanned using an OCR reader to the computer, they are automatically converted into pixels. Consequently, the mentioned 16 statistical attributes are recorded to the computer too.
Note that the concentration of black pixels across the various areas of the box should provide a way to differentiate among 26 letters of the alphabet using an OCR or a machine learning algorithm to be trained.
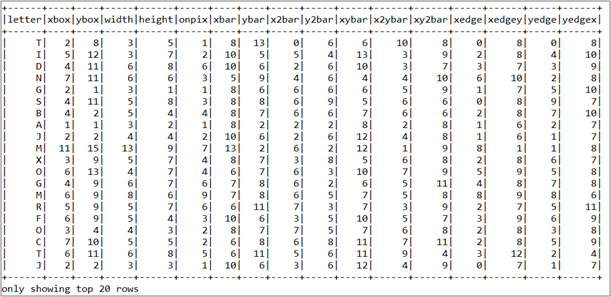
Figure 2: The snapshot of the dataset shown as Data Frame
Recall that SVM, Naïve Bayesian-based classifier or any other classifier algorithms (along with their associated learners) requires all the features to be numeric. Moreover, each feature is scaled to a fairly small interval. Also, SVM works well on dense vectorised features and consequently will poorly perform against the sparse vectorised features. In this case, every feature/variable is an integer. Therefore, we do not need to convert any values into numbers. On the other hand, some of the ranges for these integer variables appear fairly wide. In most of the practical cases, it might require that we need to normalize the data against all the features points. In short, we do need to convert the dataset to from current tab separated OCR data to libsvm format.
Interested readers should refer the following research article for getting in depth knowledge: Chih-Chung Chang and Chih-Jen Lin, LIBSVM: a library for support vector machines, ACM Transactions on Intelligent Systems and Technology, 2:27:1--27:27, 2011. The Software is available at [13].
Interested readers can refer a public script provided on my GitHub repository at [14] that directly converts CSV to libsvm format. Just properly show the input and output file path and run the script, that's all. I’m assuming that readers have downloaded the data or have converted the OCR data to LIBSVM format using my GitHub script or using their own script. Nevertheless, I have uploaded the original and converted dataset along with source codes (including Maven friendly pom.xml file) that can be downloaded from here.
Character Prediction With Spark
The Spark based solution consists of several steps including dataset loading, parsing the data, training and testing set preparation, RF model training, preparing predictions relation statistics and model evaluation that are go as follows:
Step-1: Loading required packages and APIs
import java.util.HashMap;
import org.apache.spark.api.java.JavaPairRDD;
import org.apache.spark.api.java.JavaRDD;
import org.apache.spark.api.java.function.Function;
import org.apache.spark.api.java.function.PairFunction;
import org.apache.spark.mllib.evaluation.MulticlassMetrics;
import org.apache.spark.mllib.regression.LabeledPoint;
import org.apache.spark.mllib.tree.RandomForest;
import org.apache.spark.mllib.tree.model.RandomForestModel;
import org.apache.spark.mllib.util.MLUtils;
import org.apache.spark.sql.SparkSession;
import com.example.SparkSession.UtilityForSparkSession;
import scala.Tuple2;Step-2: Create a Spark session
static SparkSession spark = SparkSession
.builder()
.appName("RandomForestModel")
.master("local[*]")
.config("spark.sql.warehouse.dir", "E:/Exp/") // set the SQL warehouse accordingly.
.getOrCreate();Step-3: Loading and parsing the dataset
String datapath = "input/Letterdata_libsvm.data";
JavaRDD<LabeledPoint> data = MLUtils.loadLibSVMFile(spark.sparkContext(), datapath).toJavaRDD();Step-4: Split the data into training and test sets
JavaRDD<LabeledPoint>[] splits = data.randomSplit(newdouble[]{0.70, 0.30}); // 70% as training and 30% as test set
JavaRDD<LabeledPoint> trainingData = splits[0];
JavaRDD<LabeledPoint> testData = splits[1];Step-5: Train the random forest model
At first, prepare the related parameters to train the model as follows:
Integer numClasses = 26; // 26 alphabets means 26 classes
HashMap<Integer, Integer> categoricalFeaturesInfo = new HashMap<>(); // Empty categoricalFeaturesInfo indicates all features are continuous.
Integer numTrees = 10; // Deafult is 5 but it is better practice to have more trees. If >1 then it is considered as a forest.
String featureSubsetStrategy = "auto"; // Let the algorithm choose the best feature subset strategy.
String impurity = "gini"; // For information gain
Integer maxDepth = 20; //Maximum depth of the tree
Integer maxBins = 40; // Number of maximum beans to be used
Integer seed = 12345L; // Random seedNow train the model using the above parameters as follows:
final RandomForestModel model = RandomForest.trainClassifier(trainingData,
numClasses,
categoricalFeaturesInfo,
numTrees,
featureSubsetStrategy,
impurity,
maxDepth,
maxBins,
seed);Step-6: Evaluate the model
We will evaluate the random forest model in two levels. Level-1 is weaker which returns only the test error as discussed above theory part. Now at first we evaluate the model on test instances as follows:
JavaPairRDD<Double, Double> predictionAndLabel =
testData.mapToPair(new PairFunction<LabeledPoint, Double, Double>() {
@Override
public Tuple2<Double, Double> call(LabeledPoint p) {
returnnew Tuple2<>(model.predict(p.features()), p.label());
}
});Now compute and print the test error as follows:
Double testErr =
1.0 * predictionAndLabel.filter(new Function<Tuple2<Double, Double>, Boolean>() {
@Override
public Boolean call(Tuple2<Double, Double> pl) {
return !pl._1().equals(pl._2());
}
}).count() / testData.count();
System.out.println("Test Error: " + testErr);The above println() method prints the follows value on the console:
Test Error: 0.00497429945282706
This value signifies that the test error is very low that also signifies that the classification accuracy is pretty high.
Now let’s evaluate the model using more robust statistics (i.e, evaluation level-2). Now at first we evaluate the model on test instances as follows:
JavaRDD<Tuple2<Object, Object>> predictionAndLabels = testData.map(
new Function<LabeledPoint, Tuple2<Object, Object>>() {
public Tuple2<Object, Object> call(LabeledPoint p) {
Double prediction = model.predict(p.features());
returnnew Tuple2<Object, Object>(prediction, p.label());
}
}
);Now let's compute and get the evaluation metrics as follows:
MulticlassMetrics metrics = new MulticlassMetrics(predictionAndLabels.rdd());
System.out.println(metrics.confusionMatrix());
System.out.println(metrics.confusionMatrix());
double precision = metrics.precision(metrics.labels()[0]);
double recall = metrics.recall(metrics.labels()[0]);
double f_measure = metrics.fMeasure();
double query_label = 8.0;
double TP = metrics.truePositiveRate(query_label);
double FP = metrics.falsePositiveRate(query_label);
double WTP = metrics.weightedTruePositiveRate();
double WFP = metrics.weightedFalsePositiveRate();
System.out.println("Precision = " + precision);
System.out.println("Recall = " + recall);
System.out.println("F-measure = " + f_measure);
System.out.println("True Positive Rate = " + TP);
System.out.println("False Positive Rate = " + FP);
System.out.println("Weighted True Positive Rate = " + WTP);
System.out.println("Weighted False Positive Rate = " + WFP);If you see the Figure 2 carefully, you will find that the character ‘I’ was actually encoded as 8.0 using our script. In a nutshell, the above metrics actually, predict the label (i.e., class) of 8.0. I received the following results:
Precision = 1.0
Recall = 1.0
F-measure = 0.995025700547173
True Positive Rate = 1.0
False Positive Rate = 0.0
Weighted True Positive Rate = 0.995025700547173
Weighted False Positive Rate = 1.1034125704803483E-4Conclusion
This way the RF can be used as a classifier. Please note due to the random nature of the data, you might get different prediction value. Readers are suggested to find more on machine learning algorithms with Spark MLlib at [9]. Moreover, a recent book titled “Large Scale Machine Learning with Spark” would be a good starting point from the technical as well as theoretical perspective to learn machine learning algorithms with latest Spark release (i.e., Spark 2.0.0) [10]. In next article, I will show how to use the RF as a regressor for the regression related task. The maven friendly pom.xml file, associated source codes and datasets can be downloaded from my GitHub repository here.
Opinions expressed by DZone contributors are their own.

Comments