Demystifying Dynamic Programming: From Fibonacci to Load Balancing and Real-World Applications
This article discusses when and why to employ DP and its advantages over other coding patterns. We will also discuss real-world applications of Dynamic Programming.
Join the DZone community and get the full member experience.
Join For FreeDynamic Programming (DP) is a technique used in computer science and mathematics to solve problems by breaking them down into smaller overlapping subproblems. It stores the solutions to these subproblems in a table or cache, avoiding redundant computations and significantly improving the efficiency of algorithms. Dynamic Programming follows the principle of optimality and is particularly useful for optimization problems where the goal is to find the best or optimal solution among a set of feasible solutions.
You may ask, I have been relying on recursion for such scenarios. What’s different about Dynamic Programming?
Recursion also involves breaking down a problem into smaller subproblems and solving them recursively. Recursion is often simple and elegant but can suffer from efficiency issues, particularly if there are redundant calculations.
For example, consider computing the Fibonacci sequence. The Fibonacci sequence is defined by the recurrence relation:
Here’s the recursion tree for the solution to this problem with n = 5:
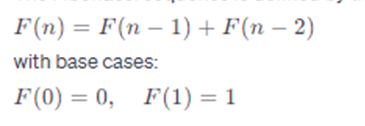

We can see above that fib(3) is evaluated twice, fib(2) is evaluated thrice, fib(1) is evaluated five times, and fib(0) is evaluated thrice. These are repeated overlapping subproblems. We can use the dynamic programming pattern to save the result once and use it wherever the subproblem is repeated.
Total recursive calls made for fib(5) --> 15 and the Time Complexity --> O (2n)
The naive recursive solution to compute Fibonacci numbers has exponential time complexity due to redundant calculations. Dynamic Programming can optimize this by storing the results of subproblems.
In Dynamic Programming, there are two approaches to save the computations and reuse them.
- Top-Down Approach with Memoization
- Bottom-Up Approach with Tabulation
Top-Down Approach With Memoization
In this approach, the problem is solved in a recursive manner, breaking it down into smaller subproblems. However, to avoid redundant calculations, the solutions to subproblems are memoized or stored in a data structure (typically a cache or a table).
Before solving a subproblem, the algorithm checks whether the solution to that subproblem is already in the memoization table.
If the solution is found in the table, it is reused; otherwise, the subproblem is solved, and the result is stored in the table for future use.
This approach is also known as "top-down" because it starts with the original problem and works its way down to smaller subproblems.
Let us solve the Fibonacci sequence problem using memoization.

As you can see in the above flowchart, we start from the top and recursively find the solutions.
Before the actual computation, we check if the solution is already cached and use it if available.
If not, we perform the computations and store the result in the cache for subsequent use.
The number of recursive calls made with memorization to find the 5th element in the Fibonacci sequence is six, i.e. (n+1), and the time complexity is O(n).
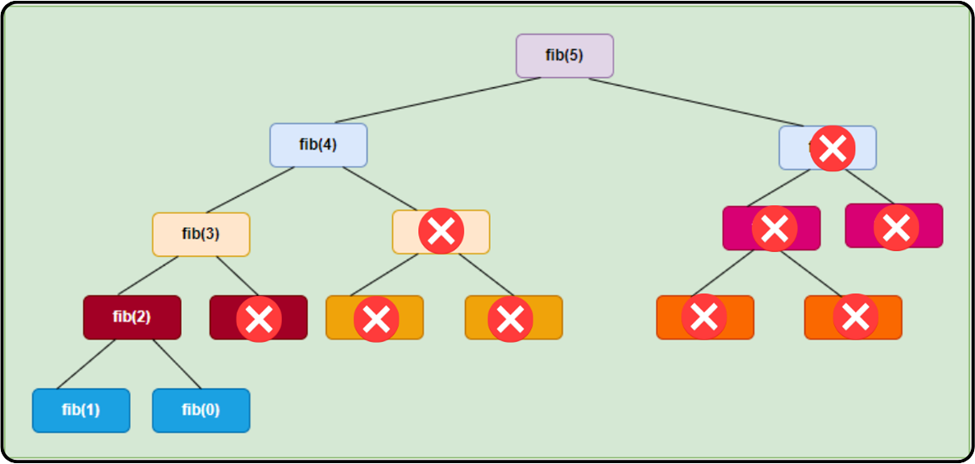
Number of Recursive Calls – (n+1) and the Time complexity O(n).
Here is the sample code using memoization.
import java.util.HashMap;
import java.util.Map;
public class TopDownFibonacci {
private static Map<Integer, Integer> memoizationCache = new HashMap<>();
public static int fibonacci(int n) {
if (n <= 1) {
return n;
}
if (memoizationCache.containsKey(n)) {
return memoizationCache.get(n);
}
int result = fibonacci(n - 1) + fibonacci(n - 2);
memoizationCache.put(n, result);
return result;
}
public static void main(String[] args) {
int n = 5;
System.out.println("Fibonacci(" + n + ") = " + fibonacci(n));
}
}
Bottom-up Approach With Tabulation
In the bottom-up approach, the problem is solved by starting with the smallest subproblems and iteratively solving larger subproblems.
The solutions to subproblems are stored in a table (tabulation) from the bottom (smallest subproblems) to the top (original problem).
The algorithm iterates through the subproblems, solving each one based on the solutions of its smaller subproblems.
This approach is also known as "bottom-up" because it starts with the smallest subproblems and builds up to the original problem.
Let’s now solve the same problem using the bottom-up approach.

In this approach, the loop iterates from 2 to n, and at each iteration, the value of dp[i] is computed using only the previously calculated values (dp[i-1] and dp[i-2]). This ensures that each Fibonacci number is computed in constant time, leading to a linear time complexity.
dp is the array used for subproblems result tabulation.
public class BottomUpFibonacci {
public static int fibonacci(int n) {
if (n <= 1) {
return n;
}
int[] dp = new int[n + 1];
dp[0] = 0;
dp[1] = 1;
for (int i = 2; i <= n; i++) {
dp[i] = dp[i - 1] + dp[i - 2];
}
return dp[n];
}
public static void main(String[] args) {
int n = 5;
System.out.println("Fibonacci(" + n + ") = " + fibonacci(n));
}
}
The time complexity of the Fibonacci sequence program using tabulation is also O(n).
Not all the recursive solutions have this characteristic of repeated overlapping subproblems.
So, how do I know if a problem can be solved using Dynamic Programming? It can be, if it meets the below characteristics.
Key Characteristics of Dynamic Programming
- Overlapping subproblems: The larger problem can be broken down into smaller subproblems, and the solutions to these subproblems are reused multiple times.
- Optimal substructure: The optimal solution to the larger problem can be constructed from the optimal solutions of its subproblems.
Recursion vs. Dynamic Programming
- Efficiency: Dynamic programming is often more efficient than pure recursion for problems with overlapping subproblems because it avoids redundant calculations.
- Memory usage: Dynamic programming may use more memory due to the memoization table, while recursion typically uses less memory.
- Readability: Recursion is often more concise and readable. Dynamic programming solutions can be more complex due to the need to manage memoization.
- Applicability: Dynamic programming is particularly suited for optimization problems with overlapping subproblems. Recursion is a more general technique applicable to a wide range of problems.
In practice, these techniques are not mutually exclusive, and some algorithms may combine both recursive and dynamic programming approaches for optimal solutions.
Many problems in the real world use the dynamic programming pattern. Let’s look at one such example: Load Balancer.
Load Balancer
Find the optimal way to handle a given workload by using servers with different workload-handling capacities. Imagine you have a set of servers, each with a different capacity to handle workloads. The goal is to distribute the incoming workload among these servers in an optimal way, ensuring that no server is overloaded and the overall system operates efficiently.
Dynamic Programming Tabulation Approach
Define the Subproblems
Break down the main problem into subproblems. In this case, the subproblems involve finding the optimal way to distribute the workload for a subset of servers or a specific workload range.
Build the Solution Bottom-up
Use a tabulation approach to iteratively solve subproblems and build up the solution to the main problem. This involves solving smaller instances of the problem and combining their solutions to solve larger instances.
Example
Let's consider a simplified scenario with three servers and their respective workload capacities:
- Server A: 10 units
- Server B: 15 units
- Server C: 20 units
Now, we have a workload of 30 units that needs to be distributed optimally among these servers. The dynamic programming algorithm, using tabulation, iteratively considers different combinations and distributions of the workload to find the optimal solution.

A sample code for the load balancer solution using Dynamic Programming:
import java.util.Arrays;
public class LoadBalancerDynamicProgramming {
public static void main(String[] args) {
int[] serverCapacities = {10, 15, 20};
int totalWorkload = 30;
int optimalDistribution = findOptimalDistribution(serverCapacities, totalWorkload);
System.out.println("Optimal Distribution: " + (optimalDistribution == Integer.MAX_VALUE ? "No valid distribution" : optimalDistribution));
}
private static int findOptimalDistribution(int[] serverCapacities, int totalWorkload) {
int[] dp = new int[totalWorkload + 1];
Arrays.fill(dp, Integer.MAX_VALUE);
dp[0] = 0;
for (int i = 1; i <= totalWorkload; i++) {
for (int capacity : serverCapacities) {
if (i >= capacity && dp[i - capacity] != Integer.MAX_VALUE) {
dp[i] = Math.min(dp[i], 1 + dp[i - capacity]);
}
}
}
return dp[totalWorkload];
}
}
Real-World Examples
Supply Chain Optimization
Amazon's vast network of warehouses, distribution centers, and delivery routes involves intricate logistical challenges. Dynamic programming could be applied to optimize routes, manage inventory, and improve overall supply chain efficiency.
Recommendation Systems
Amazon, Meta, and Google heavily rely on recommendation systems to enhance user experience and drive sales. Techniques like collaborative filtering or personalized recommendation algorithms might involve optimization aspects where dynamic programming or similar methods are applicable.
Cloud Computing Services
Amazon Web Services (AWS), MS Azure, and Google Cloud provide cloud computing services, and optimization algorithms could be employed to manage resource allocation, scaling, and other aspects to ensure efficient use of computing resources in these companies.
Search Engines
DP is used to check if white spaces can be added to a given search query to create valid words and expand the search to find all possible queries that can be formed by adding white spaces. This process is commonly known as "word segmentation" or "query expansion."
In conclusion, Dynamic Programming (DP) emerges as a powerful technique, offering a systematic and efficient approach to problem-solving in computer science and mathematics. By breaking down complex problems into smaller, overlapping subproblems and storing their solutions, DP optimizes algorithms, avoiding redundant computations and significantly improving efficiency.
Must Read for Continuous Learning
- System Design
- Head First Design Patterns
- Clean Code: A Handbook of Agile Software Craftsmanship
- Java Concurrency in Practice
- Java Performance: The Definitive Guide
- Designing Data-Intensive Applications
- Designing Distributed Systems
- Clean Architecture
- Kafka — The Definitive Guide
- Becoming An Effective Software Engineering Manager
Opinions expressed by DZone contributors are their own.

Comments