Diffie Hellman Key Exchange

In early 70’s to send a secret message, both parties (sender and receiver) had to exchange the key to encrypt and decrypt the message. Exchanging the secret key may lead to compromising the security, as while exchange this key if someone intercepted the secret key then the interceptor can decrypt all messages. This problem is called the key exchange problem in computer science. 

The key exchange problem is not just limited to communication but also arises in network communication. To solve key exchange problems, Whitfield Diffie and Martin Hellman presented the Diffie-Hellman Key Exchange algorithm in 1976. 

Diffie-Hellman Key Exchange provides a way of generating a shared key between two users in a way that communication does not reveal the secret key over a public network and some time the shared key also used for encrypting and decrypting the communication.

The Diffie-Hellman key exchange works like mixing colors by exchanging key colors.

Let’s assume we have a color. We can create a new color by adding another color to it. Now when a new color is ready it is not possible to identify the original color. That is, reverse operation is not possible.

A similar example is taken to visualize Diffie-Hellman Key Exchange algorithm.

Let’s say we have two users, Alice and Bob.

• They both agree to use random color which is known to everyone (e.g. yellow).
• They both have selected a private (secret for them) color for themselves (red and sea-green)
• Before sharing a color, both mixed their private color with public color. i.e. Alice mixed yellow color in red and Bob mixed sea green color in yellow.
• Both exchange new colors with each other.
• To make sure exchange identity, both mixed their private color in the new color which they received.
• After mixing private color both will have identical color as final color, which identifies the exchange of color is successful (securely exchange the keys).
• If a third person has intercepted the color exchange, it would be difficult to determine the secret color.

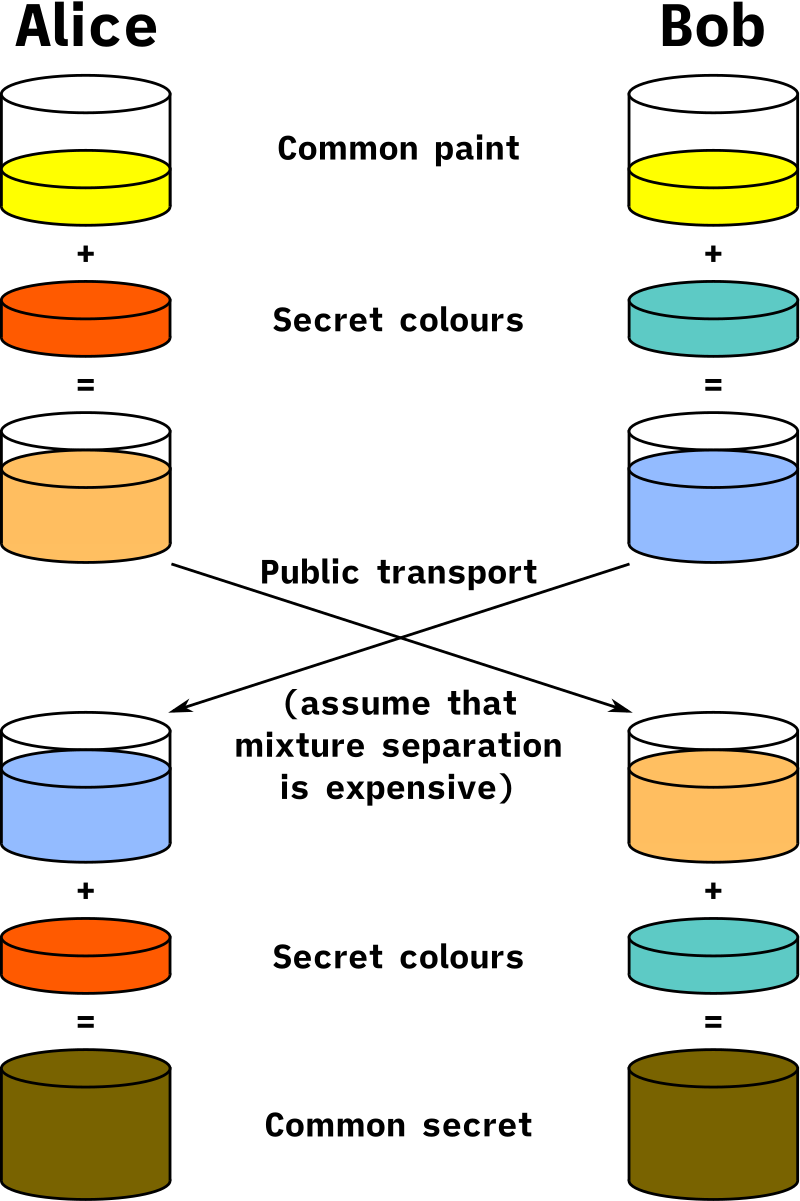
Diffie-Hellman Key Exchange is based on a similar concept, but it uses mathematics instead of color mixing.

The Math Behind the Diffie-Hellman Key Exchange

Diffie-Hellman uses modular exponentiation, which is also known as repeated sequence algorithm. For more information like how it works, refer to this link.

Modern crypto algorithms work with at least 128-bit long keys. To perform such large operation we need modular exponentiation.

Diffie-Hellman uses two numbers:

1. A Prime number 
2. The primitive root of the prime number

Let’s consider that there is a huge prime number, known to all participants, it’s public information. We call it “p,” or modulus.

There is also another public number called “g” or base, which is less than p which is the primitive root of “p.”

For example, let’s say p = 13, g = 6

The second step is both participants (Alice and Bob) will pick a secret number. Let’s say the sender's secret key is “a” and the receiver's secret key is “b," and let's say a = 3, and b = 10

Similar to color mixing, Alice and Bob uses the below equation to mix their secret keys into public numbers:

After the exchange the A and B will verify using the below equation:

If we have A = ga mod p and B = gb mod p, we can calculate gab mod p, without revealing a or b (which are called secret exponents).

This Is How It Works

• Alice and Bob agree to use two public integers: modulus p and base g (where p is prime, and g is a primitive root modulo p).
• Alice chooses a secret integer a, then calculates and sends to Bob the number A = g^a mod p.
• Bob chooses a secret integer b, then calculates and sends to Alice the number B = g^b mod p.
• Alice computes s = B^a mod p  
• Bob computes s = Ab mod p
• Alice and Bob now share a secret number without reveling it.

Diffie-Hellman Key Exchange algorithm is unaffected by sniffing attacks (data interception) but it is vulnerable to man-in-the-middle attacks (attacker secretly relays and possibly alters the communication between two parties).

For demonstration purposes, I have implemented Diffie-Hellman Key Exchange using C#.