Feature Selection Using Genetic Algorithms (GA) in R
Ever been to the Galapagos Islands? No? Well then this post is the second best thing! Read on to learn about GA and implementing them in R.
Join the DZone community and get the full member experience.
Join For FreeThis is a post about feature selection using genetic algorithms in R, in which we will review:
- What are genetic algorithms (GA)?
- GA in ML.
- What does a solution look like?
- The GA process and its operators.
- The fitness function.
- Genetics Algorithms in R.
- Trying it yourself.
- Relating concepts.
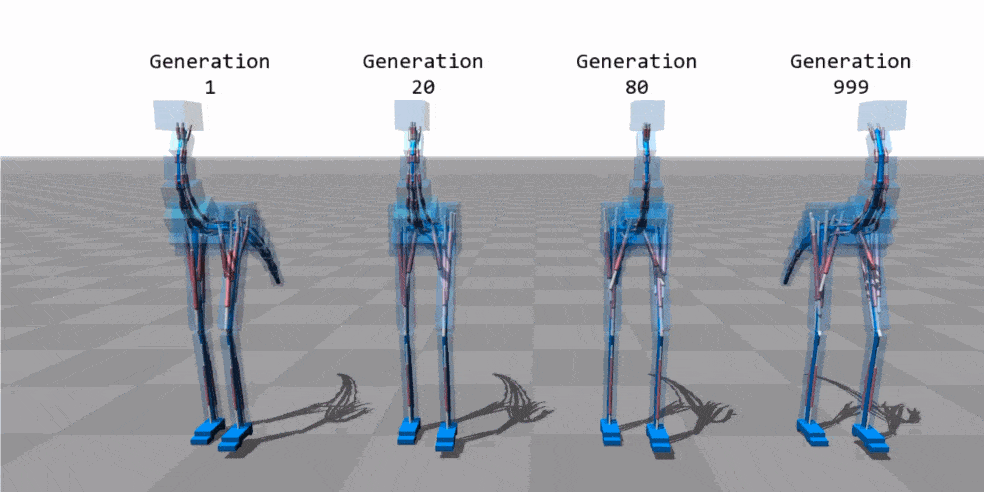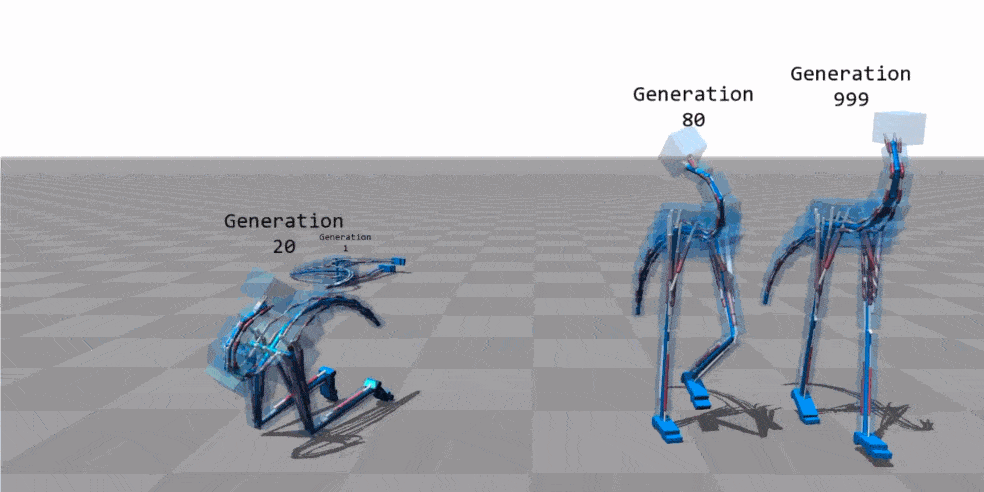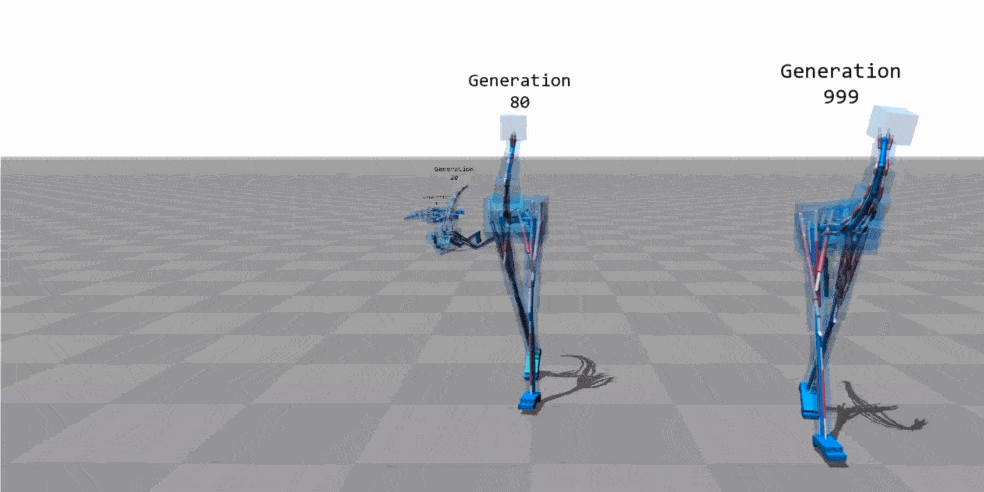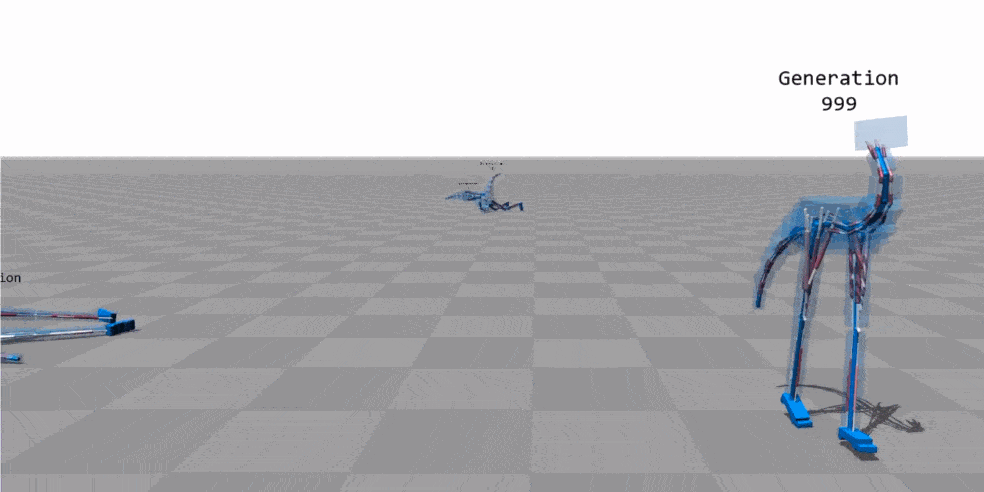
Animation source: "Flexible Muscle-Based Locomotion for Bipedal Creatures" - Thomas Geijtenbeek
[Find me on Twitter and LinkedIn]
The Idea Behind the Project
Imagine a black box which can help us to decide between an unlimited number of possibilities, with a criterion such that we can find an acceptable solution (both in time and quality) to a problem that we formulate.
What Are Genetic Algorithms?
Genetic Algorithms (GA) are a mathematical model inspired by Charles Darwin's idea of natural selection.
Natural selection preserves only the fittest individuals over generations.
Imagine a population of 100 rabbits in the year 1900. If we look at the population today, we are going to see rabbits that are fastes and more skilled at finding food than their ancestors.
GA in ML
In machine learning, one of the uses of genetic algorithms is to pick up the right number of variables in order to create a predictive model.
To pick up the right subset of variables is a problem of combinatory logic and optimization.
The advantage of this technique over others is that it allows the best solution to emerge from the best of the prior solutions. An evolutionary algorithm which improves the selection over time.
The idea of GA is to combine the different solutions generation after generation to extract the best genes (variables) from each one. That way it creates new and more fit individuals.
We can find other uses of GA such as hyper-tunning parameters, finding the maximum (or minimum) of a function, or searching for the correct neural network architecture (neuroevolution), among others.
GA in Feature Selection
Every possible solution of the GA, i.e. the selected variable, is considered as a whole, thus it will not rank variables individually against the target.
And this is important because we already know that variables work in groups.
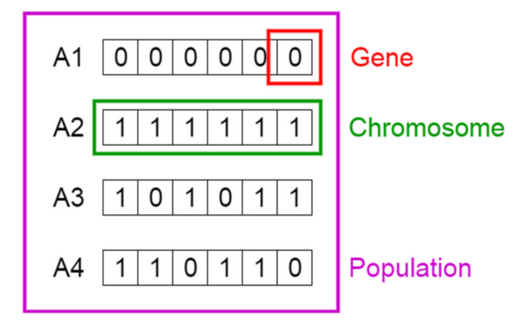
What Does a Solution Look Like?
Keeping it simple for the example, imagine we have a total of 6 variables,
One solution can be picking up three variables, let's say var2, var4, and var5.
Another solution can be var1 and var5.
These solutions are the so-called individuals or chromosomes in a population. They are possible solutions to our problem.
Credit image: Vijini Mallawaarachchi
From the image, Solution 3 can be expressed as a one-hot vector: c(1,0,1,0,1,1). Each 1 indicates the solution containing that variable. In this case: var1, var3, var5, var6.
While Solution 4 is c(1,1,0,1,1,0).
Each position in the vector is a gene.
GA Process and Its Operators
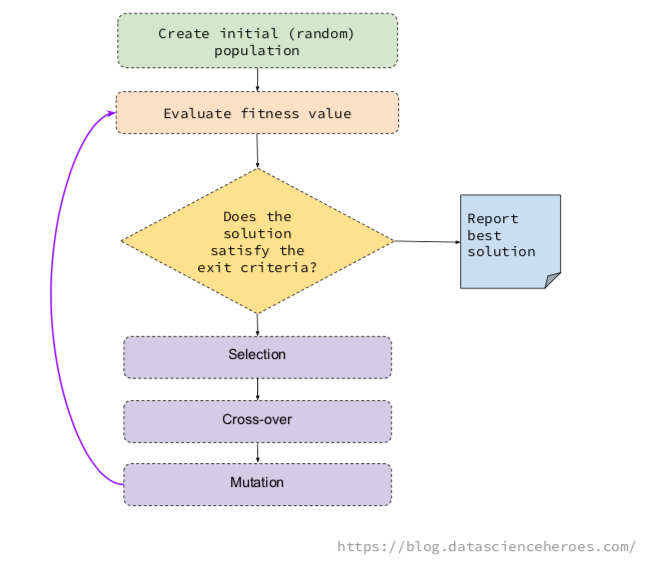
The underlying idea of a GA is to generate some random possible solutions (called population), which represent different variables, to then combine the best solutions in an iterative process.
This combination follows the basic GA operations, which are selection, mutation, and cross-over.
- Selection: Pick up the fittest individuals in a generation (i.e. the solutions providing the highest ROC).
- Cross-over: Create two new individuals, based on the genes of two solutions. These children will appear to the next generation.
- Mutation: Change a gene randomly in the individual (i.e. flip a
0to1).
The idea is that for each generation we will find better individuals, like a faster rabbit.
I recommend the post by Vijini Mallawaarachchi about how a genetic algorithm works.
These basic operations allow the algorithm to change the possible solutions by combining them in a way that maximizes the objective.
The Fitness Function
This objective maximization is, for example, to keep with the solution that maximizes the area under the ROC curve. This is defined as the fitness function.
The fitness function takes a possible solution (or chromosome, if you want to sound more sophisticated), and evaluates the effectiveness of the selection.
Normally, the fitness function takes the one-hot vector c(1,1,0,0,0,0) and creates, for example, a random forest model with var1 and var2, and returns the fitness value (ROC).
The fitness value in this code is calculated as ROC value/number of variables. By doing this, the algorithm penalizes the solutions with a large number of variables. Similar to the idea of Akaike information criterion, or AIC.
Genetics Algorithms in R!
My intention is to provide you with clean code so you can understand how it works, while at the same time getting to try new approaches, like modifying the fitness function. This is a crucial point.
To use on your own data set, make sure data_x (data frame) and data_y (factor) are compatible with the custom_fitness function.
The main library is GA, developed by Luca Scrucca. See the here for examples.
Important: The following code is incomplete. Clone the repository to run the example.
# data_x: input data frame
# data_y: target variable (factor)
# GA parameters
param_nBits=ncol(data_x)
col_names=colnames(data_x)
# Executing the GA
ga_GA_1 = ga(fitness = function(vars) custom_fitness(vars = vars,
data_x = data_x,
data_y = data_y,
p_sampling = 0.7), # custom fitness function
type = "binary", # optimization data type
crossover=gabin_uCrossover, # cross-over method
elitism = 3, # best N indiv. to pass to next iteration
pmutation = 0.03, # mutation rate prob
popSize = 50, # the number of indivduals/solutions
nBits = param_nBits, # total number of variables
names=col_names, # variable name
run=5, # max iter without improvement (stopping criteria)
maxiter = 50, # total runs or generations
monitor=plot, # plot the result at each iteration
keepBest = TRUE, # keep the best solution at the end
parallel = T, # allow parallel procesing
seed=84211 # for reproducibility purposes
)# Checking the results
summary(ga_GA_1)── Genetic Algorithm ───────────────────
GA settings:
Type = binary
Population size = 50
Number of generations = 50
Elitism = 3
Crossover probability = 0.8
Mutation probability = 0.03
GA results:
Iterations = 17
Fitness function value = 0.2477393
Solution =
radius_mean texture_mean perimeter_mean area_mean smoothness_mean compactness_mean
[1,] 0 1 0 0 0 1
concavity_mean concave points_mean symmetry_mean fractal_dimension_mean ...
[1,] 0 0 0 0
symmetry_worst fractal_dimension_worst
[1,] 0 0# Following line will return the variable names of the final and best solution
best_vars_ga=col_names[ga_GA_1@solution[1,]==1]
# Checking the variables of the best solution...
best_vars_ga[1] "texture_mean" "compactness_mean" "area_worst" "concavity_worst" 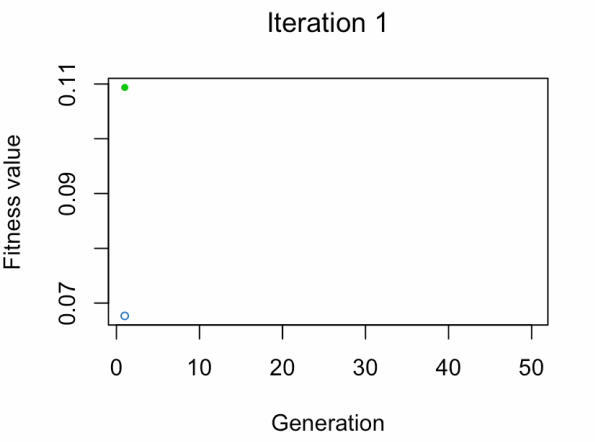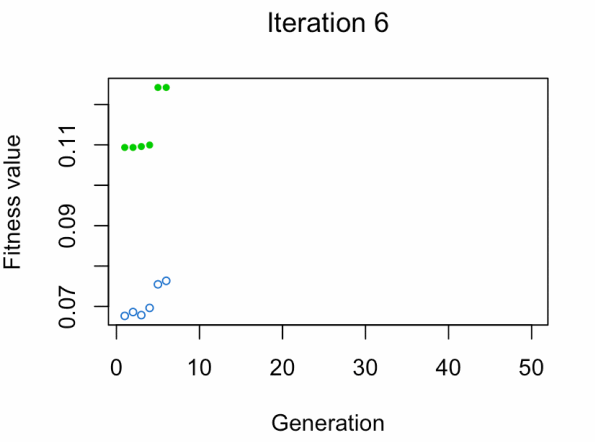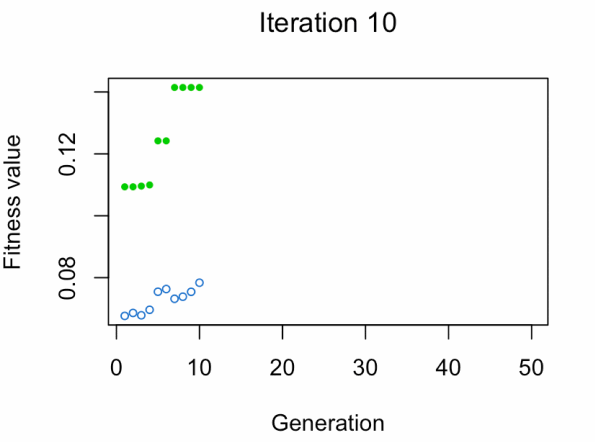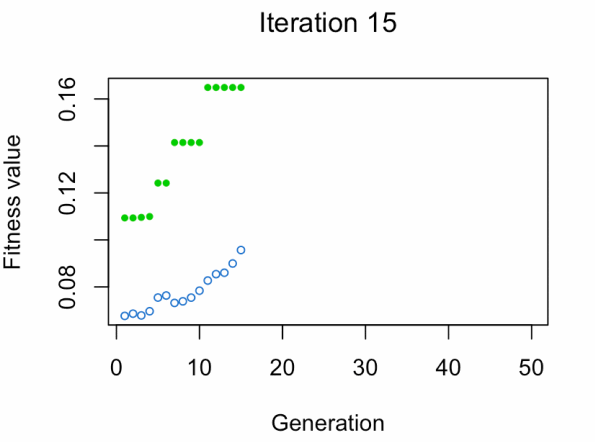
- Blue dot: Population fitness average.
- Green dot: Best fitness value.
Note: Don't expect the result that fast.
Now we calculate the accuracy based on the best selection!
get_accuracy_metric(data_tr_sample = data_x, target = data_y, best_vars_ga)[1] 0.9508279The accuracy is around 95.08%, while the ROC value is close to 0.95 (ROC = fitness value * number of variables, check the fitness function).
Analyzing the Results
I don't like to analyze the accuracy without the cutpoint (Scoring Data), but it's useful to compare with the results of this Kaggle post.
The author of the above post got a similar accuracy result using recursive feature elimination, or RFE, based on 5 variables, while our solution stays with four variables.
Try it Yourself
Try a new fitness function, some solutions still provide a large number of variables, you can try squaring the number of variables.
Another thing to try is the algorithm to get the ROC value, or even to change the metric.
Some configurations last a long time. Balance the classes before modeling and play with the p_sampling parameter. Sampling techniques can have a big impact on models. Check the Sample size and class balance on model performance post for more info.
How about changing the rate of mutation or elitism? Or trying other cross-over methods?
Increase the popSize to test more possible solutions at the same time (at a time cost).
Feel free to share any insights or ideas to improve the selection.
Clone the repository to run the example.
Relating Concepts
There is a parallelism between GA and deep learning, the concept of iteration and improvement over time is similar.
I added the p_sampling parameter to speed up things. And it usually accomplishes its goal. Similar to the batch concept used in deep learning. Another parallel is between the GA parameter run and the early stopping criteria in the neural network training.
But the biggest similarity is both techniques come from observing the nature. In both cases, humans observed how neural networks and genetics work, and create a simplified mathematical model that imitate their behavior. Nature has millions of years of evolution, why not try to imitate it?
--
I tried to be brief about GA, but if you have any specific question on this vast topic, please leave it in the comments.
Thanks for reading!
Find me on Twitter and Linkedin.
Want to learn more? �� Data Science Live Book
Published at DZone with permission of Pablo Casas, DZone MVB. See the original article here.
Opinions expressed by DZone contributors are their own.

Comments