Markov Models and Hidden Markov Models
Join the DZone community and get the full member experience.
Join For FreeIn this post will give introduction to Markov models and Hidden Markov models as mathematical abstractions, with some examples.
In probability theory, a Markov model is a stochastic model that assumes the Markov property. A stochastic model models a process where the state depends on previous states in a non-deterministic way. A stochastic process has the Markov property if the conditional probability distribution of future states of the process.
| System state is fully observable | System state is partially observable | |
|
System is autonomous |
Markov chain | Hidden Markov model |
System is controlled |
Markov decision process | Partially observable Markov decision process |
Markov chain
A Markov chain named by Andrey Markov, is a mathematical system that representing transitions from one state to another on a state space. The state is directly visible to the observer. It is a random process usually characterized as memoryless: the next state depends only on the current state and not on the sequence of events that preceded it. This specific kind of "memorylessness" is called the Markov property.
Let's talk about the weather. we have three types of weather sunny, rainy and cloudy.
Let's assume for the moment that the weather lasts all day and it does not change from rainy to sunny in the middle of the day.
Weather prediction is try to guess what the weather will be like tomorrow based on a history of observations of weather
simplified model of weather prediction
Wewill collect statistics on what the weather was like today based on what the weather was like yesterday the day before and so forth. We want to collect the following probabilities.
Using above expression, we can give probabilities of types of weather for tomorrow and the next day using n days of history.
The larger n will be problem in here. The more statistics we must collect Suppose that n=5 then we must collect statistics for 35 = 243 past histories Therefore we will make a simplifying assumption called the "Markov Assumption".
This is called a "first-order Markov assumption" since we say that the probability of an observation at time n only depends on the observation at time n-1. A second-order Markov assumption would have the observation at time n depend on n-1 and n-2. We can the express the joint probability using the “Markov assumption”.
So this now has a profound affect on the number of histories that we have to find statistics for, we now only need 32 = 9 numbers to characterize the probabilities of all of the sequences. (This assumption may or may not be a valid assumption depending on the situation.)
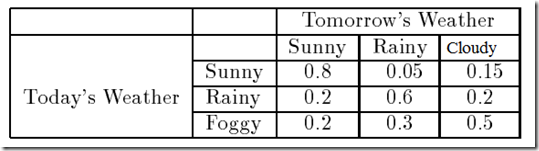
Arbitrarily pick some numbers for P (wtomorrow | wtoday).
Tabel2: Probabilities of Tomorrow's weather based on Today's Weather
“What is w0?” In general, one can think of w as the START word so P(w1w2) is the probability that w1 can start a sentence.
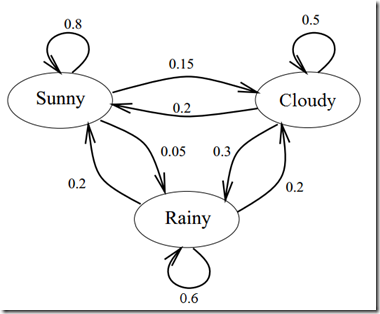
For first-order Markov models we can use these probabilities to draw a probabilistic finite state automaton.
eg:
1. Today is sunny what's the probability that tomorrow is sunny and the day after is rainy
First we translates into
- P(w2= sunny,w3=rainy|w1=sunny)
| P(w2= sunny,w3=rainy|w1=sunny) | = P(w2=sunny|w1=sunny) * P(w3=rainy|w2=sunny,w3sunny) |
| = P(w2=sunny|w1=sunny) * P(w3=rainy|w2=sunny) | |
| = 0.8 * 0.05 | |
| =0.04 |
Hidden Markov model
A hidden Markov model (HMM) is a statistical Markov model in which the system being modeled is assumed to be a Markov process with unobserved (hidden) states. A HMM can be considered the simplest dynamic Bayesian network. Hidden Markov models are especially known for their application in temporal pattern recognition such as speech, handwriting, gesture recognition, part-of-speech tagging, musical score following, partial discharges and bioinformatics.
Example
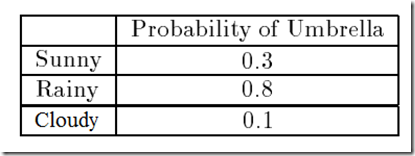
Well suppose you were locked in a room for several days and you were asked about the weather outside The only piece of evidence you have is whether the person who comes into the room carrying your daily meal is carrying an umbrella or not.
Table 3: Probabilities of Seeing an Umbrella
The equation for the weather Markov process before you were locked in the room.
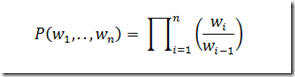
Now we have to factor in the fact that the actual weather is hidden from you We do that by using Bayes Rule.
Where ui is true if your caretaker brought an umbrella on day i and false if the caretaker did not. The probability P(w1,..,wn) is the same as the Markov model from the last section and the probability P(u1,..,un) is the prior probability of seeing a particular sequence of umbrella events.
The probability P(w1,..,wn|u1,..,un) can be estimated as,
Assume that for all i given wi, ui is independent of all uj and wj. I and J not equal
Next post will explain about “Markov decision process” and “Partially observable Markov decision process”.
Published at DZone with permission of Madhuka Udantha, DZone MVB. See the original article here.
Opinions expressed by DZone contributors are their own.

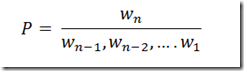
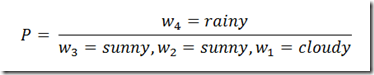
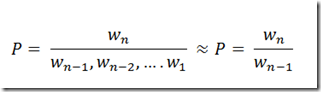
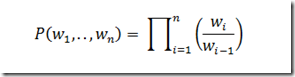
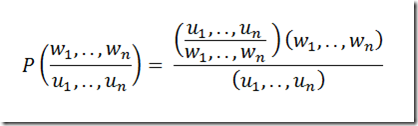
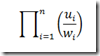
Comments