Multi-Touch Attribution Models
In this comprehensive guide, explore some of the traditional and advanced multi-touch attribution models and the algorithms behind them.
Join the DZone community and get the full member experience.
Join For FreeMulti-Touch Attribution (MTA) is an advanced approach in digital marketing analytics that assigns credit to each touchpoint a consumer interacts with during their journey towards a conversion. Unlike traditional models that attribute conversion success to a single touchpoint, MTA recognizes the complexity of consumer behavior by analyzing how different channels and interactions contribute to the final outcome. This method is increasingly crucial in a multi-channel marketing landscape as it provides more accurate insights into the effectiveness of various marketing strategies and campaigns.
In the technical realm, MTA employs algorithms and statistical methods to distribute credit for conversion across multiple customer interactions, ranging from first exposure to the final conversion action. In this article, we are going to explore some of the traditional and advanced multi-touch attribution models and the algorithms behind them.
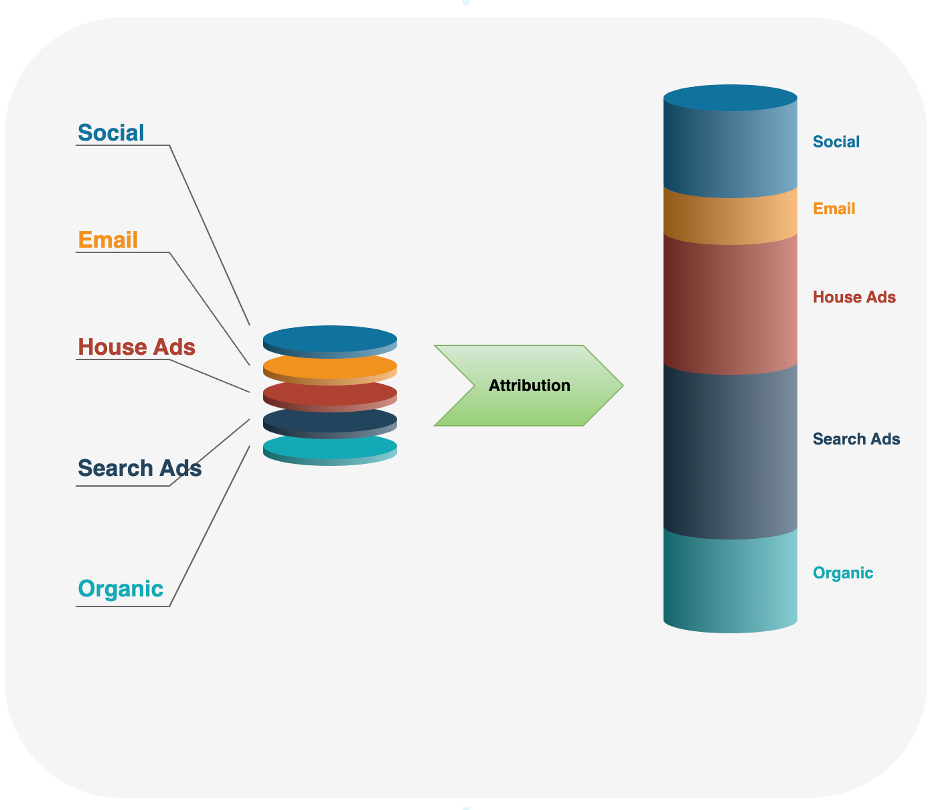
Figure 1: Attribution model assigns weights to each channel
Traditional Models
Assume we have a series of n touchpoints leading to a conversion, and let C represent the total conversion value. The contribution value assigned to each touchpoint i will be denoted as Vi. Below are the various traditional attribution models
- Last-click attribution assigns full credit for a conversion to the final touchpoint before a purchase. While straightforward, its major flaw is the disregard for all preceding customer interactions, potentially undervaluing the importance of early engagement and awareness initiatives in the marketing funnel.

- First-click attribution credits the initial interaction in the customer's journey with the entire conversion. This approach overlooks the contribution of subsequent touchpoints, often resulting in a skewed understanding of mid-funnel and closing strategies' effectiveness.

- Linear attribution evenly distributes credit across all touchpoints. However, this model's critical limitation is its failure to acknowledge the varying influence of different interactions, potentially oversimplifying the impact of each marketing effort. Credit is evenly distributed across all touchpoints.

- Position-based (U-shaped) attribution emphasizes the first and last interactions (usually 40% credit each), with the rest spread across other touchpoints. This model might not accurately capture the significance of mid-funnel activities and can oversimplify complex customer journeys. Most credit goes to the first and last touchpoints, with the rest distributed evenly among the middle touchpoints.

- W-Shaped Attribution: An extension of the U-shaped model, it also gives additional weight to the mid-funnel touchpoint (typically a lead conversion), along with the first and last touchpoints.
These traditional attribution models, while providing basic frameworks for understanding marketing impact, often fall short of accurately reflecting the intricate, multi-faceted nature of modern consumer journeys. They tend to either oversimplify the process or bias certain touchpoints, leading to potentially skewed marketing insights and decisions. As the digital landscape evolves, more sophisticated and nuanced approaches like Multi-Touch Attribution are gaining prominence to address these limitations.
Advanced Models
Time Decay Attribution Model
The Time Decay Attribution Model is a popular method used in marketing analytics to attribute credit for conversions based on the timing of customer touchpoints. This model operates on the principle that touchpoints closer in time to the conversion are more influential than earlier ones.
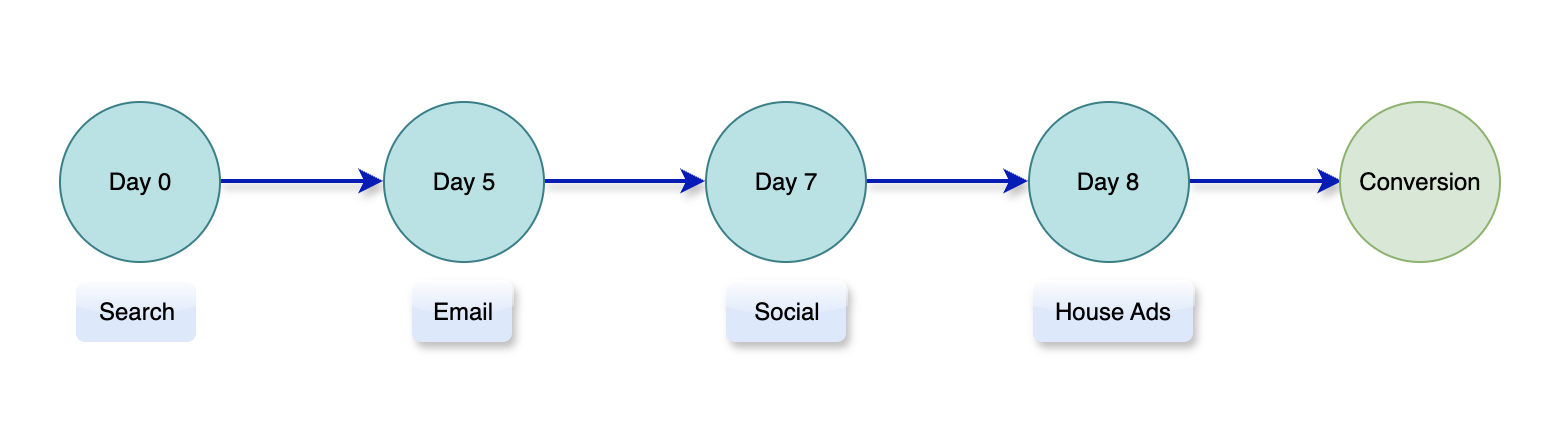
Concept
The Time Decay model assigns more credit to marketing interactions that occur closer to the time of conversion. It's based on the rationale that these later interactions are likely more impactful in influencing the customer's final decision. It is particularly useful in long sales cycles where multiple touchpoints occur over an extended period, allowing marketers to weigh recent interactions more heavily.
Approach
- Touchpoint identification: All touchpoints along the customer journey, from the first interaction to the conversion, are identified.
- Time-based weighting: Each touchpoint is assigned a weight that increases as it gets closer to the conversion event. The weighting typically follows an exponential or logarithmic function, where the increase in credit allocation accelerates as the touchpoint gets closer to the moment of conversion.
- Credit allocation: The model calculates the attribution by distributing the total conversion value among the touchpoints, based on their assigned weights.
A common approach to represent the Time Decay model is through an exponential decay function. If t represents the time of a touchpoint and T is the time of conversion, the weight W assigned to a touchpoint can be expressed as:
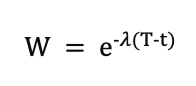
Where:
- e is the base of the natural logarithm.
- λ is a decay rate constant that determines how rapidly the weight of a touchpoint decreases over time. A higher λ means a faster decay.
Markov Chain Attribution Models
The Markov Chain Model in MTA is a sophisticated method used to evaluate the effectiveness of different marketing touchpoints in a customer's journey. In MTA, the Markov Chain Model treats the customer journey as a sequence of states, corresponding to various touchpoints. The key property of a Markov Chain is that the probability of moving to the next state depends only on the current state, not on the previous states. Each touchpoint in a customer's journey is a state in the Markov Chain. The model analyzes transitions between these states to understand how customers move through the sales funnel and how each touchpoint influences their journey toward conversion.
Background
Markov Chains were developed by Andrey Markov in the early 20th century. Their adoption in marketing attribution is a relatively recent innovation, leveraging their capacity to model complex, non-linear customer journeys. The use of Markov Chains in marketing attribution became prominent with the rise of multi-channel digital marketing strategies. In an environment where customers interact with multiple marketing touchpoints across different channels before converting, traditional attribution models like last-click or first-click became insufficient. Markov Chain models offered a more dynamic and holistic view.
Algorithmic Approach
- Defining states: Each unique touchpoint, along with the start, conversion, and non-conversion, is defined as a state.
- Transition probability matrix: Construct a matrix that represents the probabilities of transitioning from one state (touchpoint) to another, based on historical data.
- Building the chain: Use the transition probabilities to model the customer journey as a Markov Chain.
- Calculating conversion probabilities: Compute the likelihood of reaching the conversion state from each touchpoint.
- Assessing touchpoint influence: Analyze the impact of removing individual touchpoints on the overall conversion probability, indicating their contribution to the journey.
The table below shows the customer journey of four customers and its conversion factor.
| Customer | Channel | Conversion |
| A | Email ->House Ads | No |
| B | Search Ads -> House Ads | Yes |
| C | House Ads | No |
| D | Search Ads -> Social | Yes |
The customer journey of the table above can be visualized as a Directed Acyclic Graph (DAG) with probability for each transition as below.
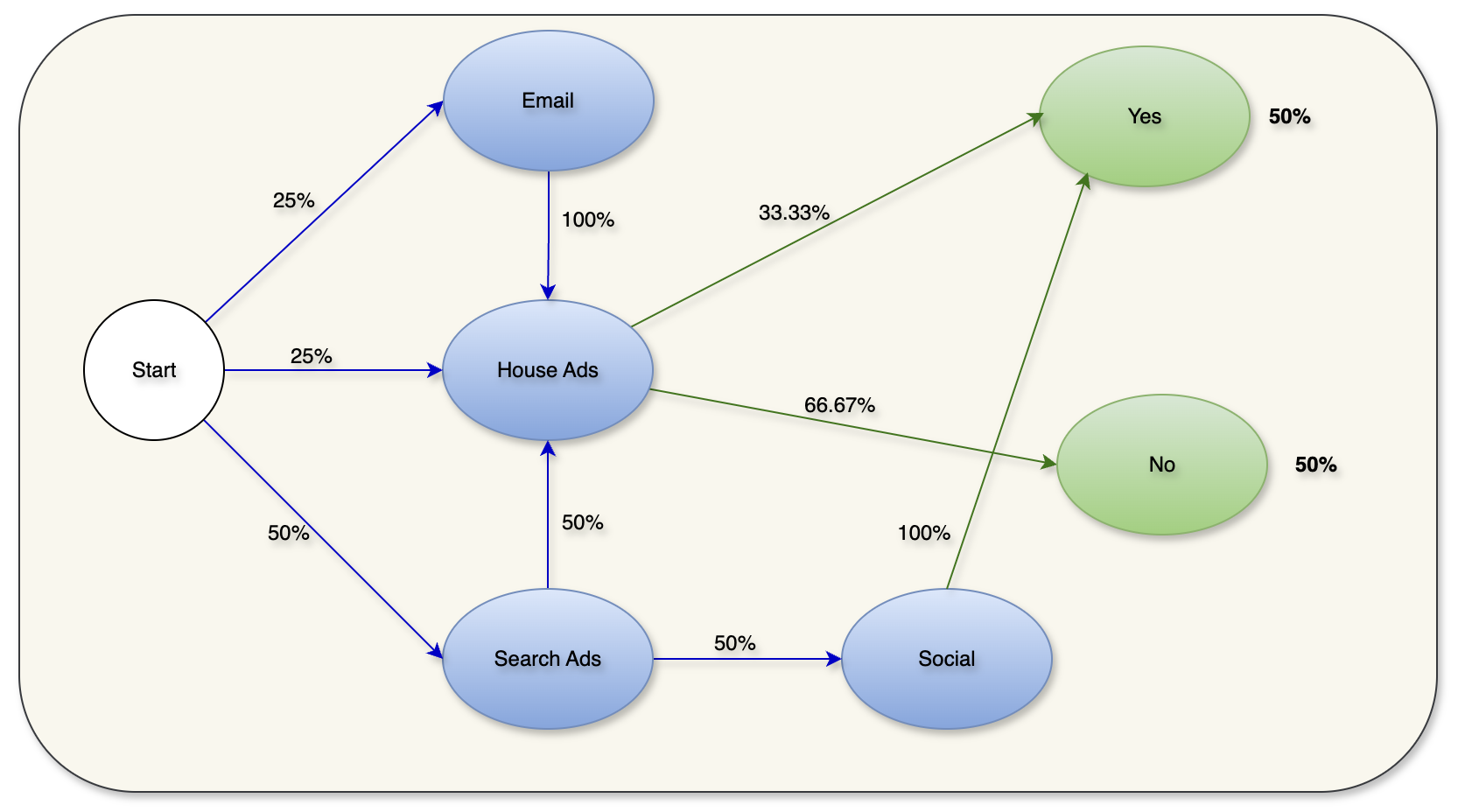
Figure 2: Customer Journey DAG
Removal Effect
An important aspect of Markov chain attribution is how the removal of a given touchpoint from the graph affects the likelihood of conversion.
Let’s remove the Email node from the graph above to understand this behavior.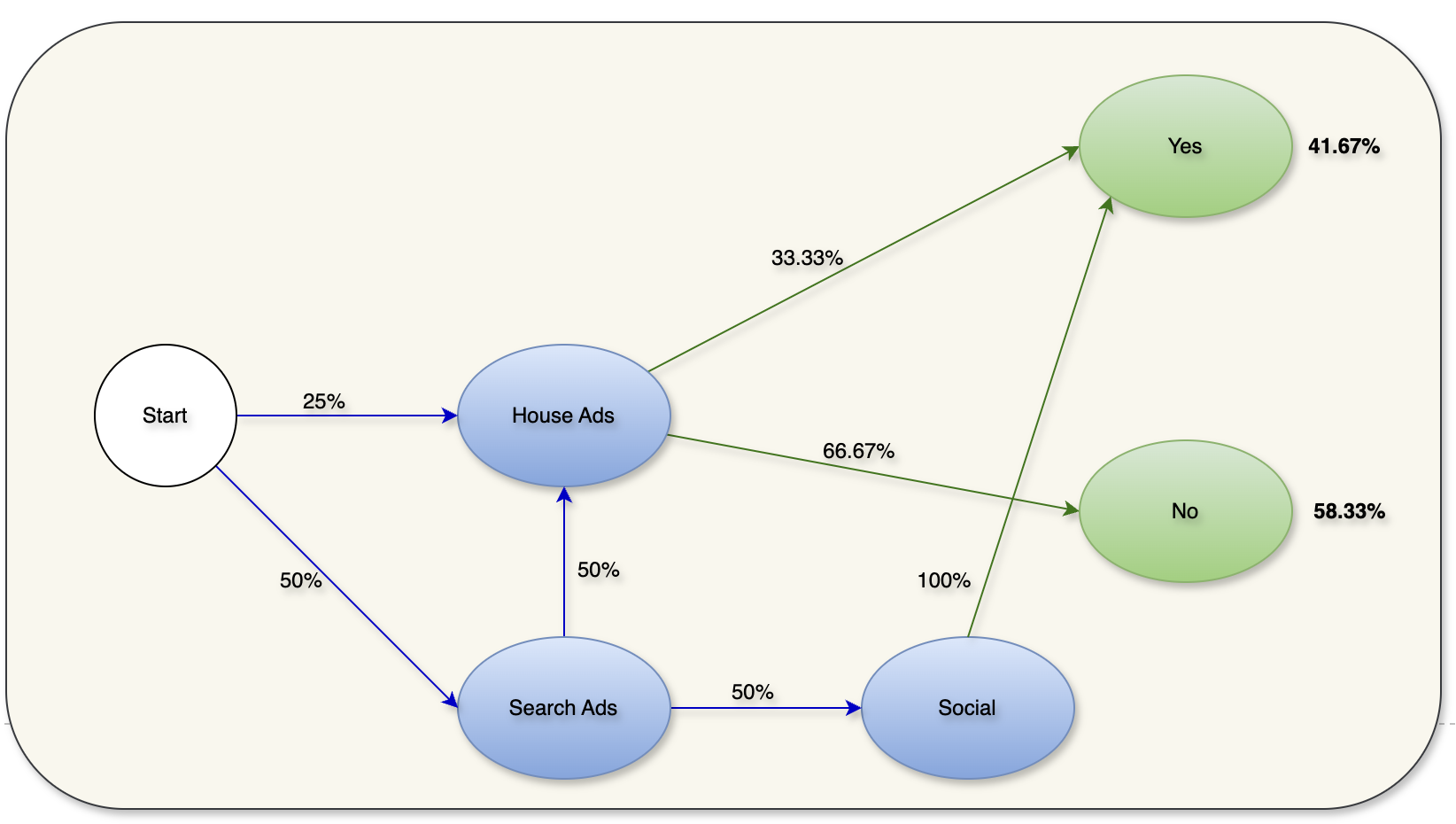
Figure 3: DAG with Email node removed
By removing the email, the conversion probability was reduced to 41.67% from 50%. Now the removal effect of the channel can be calculated using the formula below:

Based on the above formula, the conversion probability of Email can be calculated as:
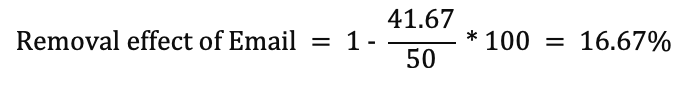
Similarly, the removal effect of other channels can be calculated using the above formula and the share of each channel can be calculated as follows:

| Channel | Conversion Probability | Removal Effect | Share |
| House Ads | 25% | 50% | 0.273 |
| Search Ads | 16.67% | 66.67% | 0.364 |
| Social | 25% | 50% | 0.273 |
| 41.67% | 16.67% | 0.090 |
Markov Chain Limitations
- Markov Chains assume that the next state (or touchpoint) only depends on the current state and not on the history of states. This assumption might not accurately represent marketing scenarios where the effect of a touchpoint could depend on previous interactions.
- The model often overlooks the influence of one channel on the effectiveness of another, potentially underestimating the synergistic or suppressive effects between different marketing channels.
- Markov Chain models require comprehensive and granular data on customer interactions across all channels and touchpoints.
Shapley Value Attribution Model
The Shapley Value Model, originating from cooperative game theory, offers a unique and equitable approach to MTA in marketing. It allocates credit to each touchpoint in a way that fairly represents its contribution to the overall success of a marketing campaign. Its goal is a fair attribution method that considers all possible combinations of touchpoints, ensuring each one gets credit proportional to its impact.
Concept and Background
Developed by Lloyd Shapley in 1953, the Shapley Value is a solution concept in cooperative game theory. It's designed to fairly distribute the payoff among players who cooperate and contribute differently to the coalition. In the scenario of a cooperative game where multiple players join forces to create coalitions, thereby increasing the chances of a successful outcome (or payoff), the Shapley value offers a method for equitably distributing the payoff among the participants.
At its core, the Shapley value calculates the average contribution of each player to the coalitions they participate in. This calculation takes into account the variability in the influence (or worth) each player brings and the order in which they join the coalitions, considering that every sequence of joining has an equal chance of occurring. Therefore, players are compensated based on their contribution across all possible permutations. When applied to marketing analytics, the players in this scenario are the various campaign channels, and the coalitions represent the different ways these channels interact and engage with accounts throughout the customer's journey. Utilizing cooperative game theory and the Shapley value, we can achieve a stable and fair measure of each channel’s influence, allocating credit for sales conversions among them proportionally to their individual contributions to the overall outcome.
Algorithmic Approach
- Enumerate all possible coalitions: List all possible combinations (subsets) of touchpoints that might lead to a conversion.
- Calculate the payoff of each coalition: Determine the value (e.g., conversion rate) that each subset of touchpoints achieves.
- Distribute value among touchpoints: For each touchpoint, calculate its contribution across all possible coalitions it's part of, based on the difference it makes to the coalition’s value.
The Shapley Value for a touchpoint is calculated using the formula:
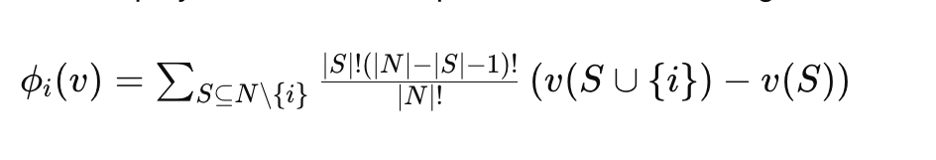
Where:
- ϕi(v) is the Shapley Value for touchpoint i.
- N is the set of all touchpoints.
- S is a subset of touchpoints excluding i.
- v(S) is the payoff (value) of the subset S.
- The sum is taken over all subsets S of N that don't include i.
Let’s take the example of touchpoints involved in conversion:
- N = { Search Ads, Social, Email }
Following is the ratio of each Coalition resulted in conversion:
| Coalition | Channels | Ratio |
| S1 | 0.04 | |
| S2 | Search Ads | 0.12 |
| S3 | Social | 0.08 |
| S4 | Email + Search Ads | 0.17 |
| S5 | Social + Search Ads | 0.22 |
| S6 | Email + Social | 0.11 |
| S7 | Search + Social + House Ads | 0.26 |
The payoff or worth of each coalition is determined by the characteristic function. In this example, the worth is represented as the sum of the conversion ratio of each channel in a coalition.
To find the payoff value of Coalition S5, use:
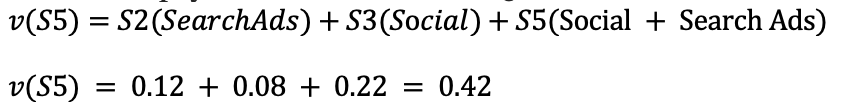
So the payoff of each coalition can be calculated as shown below:
| Function | Channels | Calculation | Payoff |
| v(S1) | S1 | 0.04 | |
| v(S2) | Search Ads | S2 | 0.12 |
| v(S3) | Social | S3 | 0.08 |
| v(S4) | Email + Search Ads | S1 + S2 + S4 | 0.33 |
| v(S5) | Social + Search Ads | S2 + S3 + S5 | 0.42 |
| v(S6) | Email + Social | S1 + S3 + S6 | 0.23 |
| v(S7) | Search + Social + House Ads | S1+ S2 + S3 + S4 + S5 + S6 | 1.0 |
Understanding the value contributed by each coalition allows for the calculation of Shapley values. These are determined by averaging the incremental contribution (marginal contribution) of each channel across all possible sequences of coalition formation. Essentially, the Shapley value method offers a systematic approach to apportion the total value generated by the grand coalition (the collective payoff) among the three channels. This approach ensures a fair distribution based on the unique contribution each channel makes to the overall outcome.
Indeed, the motivation behind the formulation of Shapley Values lies in accounting for the specific timing at which each channel or touchpoint joins a coalition. This timing is crucial because it affects the player's marginal contribution to the overall outcome. In essence, the Shapley Value method is about calculating each channel's incremental contribution, averaged across all potential sequences in which the channel or touchpoint could join the group. If the channel or touchpoint comes first, its individual payoff is considered a marginal contribution, if it comes later in the order, its subset of coalition including the prior touch points in the sequence minus the one without the current channel or touch point would be considered as its marginal contribution for the coalition. The Shapley value is the average expected marginal contribution of one channel or touchpoint after all possible combinations have been considered.
In the scenario you described, this involves simulating every possible order in which the touchpoints (Email, Social, and Search Ads) could engage with the customer. For each of these sequences, you would assess the additional value (marginal payoff) brought by each touchpoint when it's added to the sequence. Then, by averaging these incremental values across all sequences, you obtain the Shapley Value for each touchpoint.
This method ensures a fair and comprehensive evaluation of each touchpoint’s contribution by considering every possible way they could interact in the customer's journey, thereby reflecting their true value in the grand scheme of the marketing strategy.
Let’s consider the grand coalition S7 and find the Shapley value to distribute the payoff to each channel based on the arrival order of each channel.
| Arrival Order | Email Marginal Contribution | Social Marginal Contribution | Search Ads Marginal Contribution |
| Email + Social + Search | v(S1) = 0.04 | v(S6) – v(S1) = 0.19 | v(S7 ) – v(S6) = 0.77 |
| Email + Search + Social | v(S1) = 0.04 | v(S7 ) – v(S4) = 0.67 | v(S4) – v(S1) = 0.29 |
| Social + Email + Search | v(S6) – v(S3) = 0.15 | v(S3) = 0.08 | v(S7 ) – v(S6) = 0.77 |
| Social + Search + Email | V(S7) – v(S5) = 0.58 | v(S3) = 0.08 | v(S5) – v(S2) = 0.30 |
| Search + Email + Social | v(S4) – v(S2) = 0.11 | v(S7 ) – v(S4) = 0.67 | v(S2) = 0.12 |
| Search + Social + Email | v(S7) – v(S5) = 0.58 | v(S5) – v(S2) = 0.30 | v(S2) = 0.12 |
| Shapley Value or Average Marginal Contribution |
0.25 | 0.332 | 0.395 |
Shapley Value Limitations
- Calculating the Shapley value can be computationally expensive, especially with a large number of players (or marketing channels). The model requires the evaluation of every possible combination of players, which grows exponentially with the number of players.
- When direct information about specific coalitions is missing, you can use available data to estimate their values. This can be done through statistical modeling, machine learning techniques, or even simpler heuristic methods.
Bayesian Probability Models
The Bayesian Attribution Model is an advanced approach within the realm of MTA that leverages Bayesian statistics to infer the impact of various marketing touchpoints on consumer behavior and conversion rates. This model is particularly notable for its ability to handle uncertainty and integrate prior knowledge into its analytical framework.
Concept and Functionality
Bayesian Attribution is rooted in Bayesian probability, which updates the probability estimate for a hypothesis as more evidence or information becomes available. This approach is particularly useful in situations where data is incomplete or uncertain. In the context of MTA, the Bayesian model assesses the probability of conversion given the exposure to different marketing touchpoints. It updates these probabilities as new data becomes available, making it a dynamic and continuously evolving model.
Algorithmic Approach
- Defining prior probabilities: Start with initial assumptions or "priors" about the effectiveness of different touchpoints. These priors can be based on historical data or expert opinion. In case of no prior data, uniform probability distribution or other statistical methods can be used. Let's assume we have prior beliefs (based on historical data or expert opinions) about the effectiveness of each channel
- Collecting data: Gather data on customer interactions with various touchpoints along their journey toward a conversion.
- Updating probabilities: As new data comes in, the model updates the probabilities using Bayes' Theorem. This theorem combines prior probabilities with new evidence to produce updated (posterior) probabilities.
- Continuous learning: The model keeps updating its understanding of touchpoint effectiveness as more interaction data is collected, refining its insights over time.
Bayesian Attribution uses Bayes' Theorem, which in its basic form is:
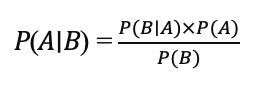
Where:
- P(A∣B) is the posterior probability (e.g., the probability of a conversion given exposure to a specific touchpoint).
- P(B∣A) is the likelihood (e.g., the likelihood of observing the data given the touchpoint's effectiveness).
- P(A) is the prior probability (initial assumption about the touchpoint's effectiveness).
- P(B) is the marginal probability of the data.
Let's explore Bayesian Multi-Touch Attribution in the customer journey example involving Display Ads, Search Ads, Social Media, and Email Ads. Let's assume we have prior beliefs (based on historical data or expert opinions) about the effectiveness of each channel.
| Channel | Prior Probabilities |
| Display Ads (A) | 0.35 |
| Search Ads (B) | 0.30 |
| Social (C) | 0.25 |
| Email (D) | 0.10 |
Calculate the likelihood based on the data points. For example, if 70% of conversions involve Search Ads in the journey, then the likelihood of Search Ads is 0.7.
| Channel | Likelihood |
| Display Ads (A) | 0.75 |
| Search Ads (B) | 0.70 |
| Social (C) | 0.50 |
| Email (D) | 0.35 |
- Marginal Probability = Sum(Likelihood of channel i X Prior Probability of Channel i); for every channel
- Marginal Probability based on above data = (0.75*0.35) + (0.7*0.3) + (0.5*0.25) + (0.35*0.1) = 0.633
Using the Bayes Theorem the posterior probability can be calculated:
| Channel | Posterior Probability |
| Display Ads (A) | (0.75*035/0.633) = 0.42 |
| Search Ads (B) | (0.7*0.3)/0.633 = 0.33 |
| Social (C) | (0.5*0.25)/0.633 = 0.20 |
| Email (D) | (0.35*0.10)/0.633 = 0.05 |
Limitations
The model's accuracy is partly dependent on the prior probabilities assigned to the effectiveness of different channels. These priors can be subjective and might skew the model if not accurately set.
Machine Learning Attribution Models
Machine learning models include regression models, decision trees, random forests, and neural networks. These models analyze complex interactions among touchpoints and can handle various types of data, including unstructured data. Capable of handling large datasets and finding non-linear relationships. They adapt as new data becomes available, providing continuously refined insights. Machine Learning (ML) algorithms have significantly advanced the field of MTA by introducing sophisticated methods to analyze complex customer journeys. These algorithms can decipher intricate patterns in large datasets, enabling marketers to understand and attribute the impact of various touchpoints more accurately.
Concept and Application
ML algorithms in MTA use data-driven approaches to model and predict the impact of each marketing touchpoint on the customer's path to conversion. They go beyond traditional rule-based attribution models by learning from data to identify how different touchpoints contribute to conversions. ML algorithms are employed to analyze the customer journey across multiple channels and touchpoints. They can handle vast and varied datasets, accounting for non-linear relationships and interactions among touchpoints.
Types of Machine Learning Algorithms
- Supervised learning:
- Concept: Supervised learning involves training a model on a labeled dataset, where the input (features) and the desired output (labels) are known. The model learns to map inputs to outputs.
- Common Algorithms: Regression models, decision trees, random forests, support vector machines, and neural networks.
2. Unsupervised learning:
- Concept: Unsupervised learning finds patterns or structures in a dataset without pre-existing labels. The algorithms discover inherent groupings or associations in the data.
- Examples: Clustering algorithms like K-means, hierarchical clustering, and principal component analysis (PCA).
Conclusion
Multi-Touch Attribution (MTA) has emerged as a crucial tool in modern marketing analytics, offering a sophisticated way to understand and quantify the impact of various touchpoints in a customer's journey. By moving beyond the limitations of traditional single-touch attribution models, MTA provides a more nuanced and comprehensive view of the effectiveness of different marketing channels and strategies.
Its ability to distribute credit for conversions more accurately across multiple interactions helps marketers optimize their campaigns, allocate budgets efficiently, and tailor customer experiences more effectively. However, the complexity and data-intensive nature of MTA models, along with the need for advanced analytical skills, mean that their implementation can be challenging. Despite these challenges, the insights gained from MTA are invaluable for businesses looking to navigate the complex, multi-channel landscape of modern digital marketing.
As technology advances and data becomes more accessible, MTA is likely to become even more integral to effective marketing strategy development and evaluation.
References
- Kakalejčík, L., Bucko, J., Resende, P.A. and Ferencova, M., 2018. Multichannel marketing attribution using Markov chains. Journal of Applied Management and Investments, 7(1), pp.49-60.
- Zhao, K., Mahboobi, S.H. and Bagheri, S.R., 2018. Shapley value methods for attribution modeling in online advertising. arXiv preprint arXiv:1804.05327.
- Sinha, R., Arbour, D. and Puli, A.M., 2022. Bayesian Modeling of Marketing Attribution. arXiv preprint arXiv:2205.15965.
- Berman, R., 2018. Beyond the last touch: Attribution in online advertising. Marketing Science, 37(5), pp.771-792.
- Romero Leguina, J., Cuevas Rumín, Á. and Cuevas Rumín, R., 2020. Digital marketing attribution: Understanding the user path. Electronics, 9(11), p.1822.
- One Feature Attribution Method to (Supposedly) Rule Them All: Shapley Values
- Data-Driven Marketing Attribution
- Markov Chain Attribution Modeling [Complete Guide]
- Markov Chain Attribution Modeling [Complete Guide]
Opinions expressed by DZone contributors are their own.

Comments