Time Series Analysis vs. DSP Terminology
Digital signal processing and time series analysis are very similar — but the terminology that they use is very different. This article is here to clarify the confusion.
Join the DZone community and get the full member experience.
Join For FreeTime series analysis and digital signal processing are closely related. Unfortunately, the two fields use different terms to refer to the same things.
Suppose you have a sequence of inputs x[n] and a sequence of outputs y[n] for integers n.
Moving Average/FIR
If each output depends on a linear combination of a finite number of previous inputs:
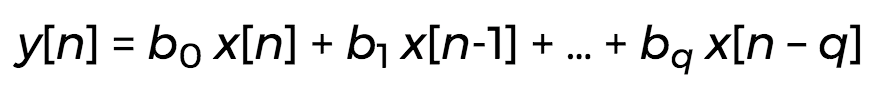
...then time series analysis would call this a moving average (MA) model of order q, provided b0 = 1. Note that this might not really be an average, i.e. the bs are not necessarily positive and don't necessarily sum to 1.
Digital signal processing would call this a finite impulse response (FIR) filter of order q.
Autoregressive/IIR
If each output depends on a linear combination of a finite number of previous outputs:
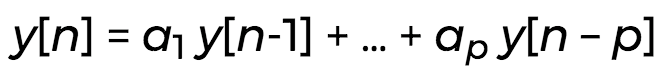
...then time series analysis would call this an autoregressive (AR) model of order p.
Digital signal processing would call this an infinite impulse response (IIR) filter of order p.
Sometimes, you'll see the opposite sign convention on the as.
ARMA/IIR
If each output depends on a linear combination of a finite number of previous inputs and outputs:
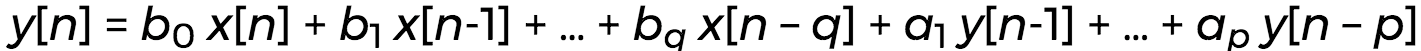
...then time series analysis would call this an autoregressive moving average (ARMA) model of order (p, q), i.e. p AR terms and q MA terms.
Digital signal processing would call this an infinite impulse response (IIR) filter with q feedforward coefficients and p feedback coefficients. Also, as above, you may see the opposite sign convention on the as.
ARMA Notation
Box and Jenkins use as for input and zs for output. We'll stick with xs and ys to make the comparison to DSP easier.
Using the backward shift operator B that takes a sample at n to the sample at n-1, the ARMA system can be written as:
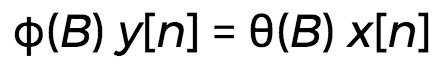
...where φ and θ are polynomials, and:
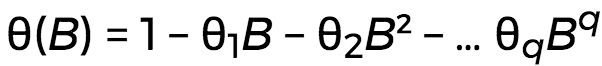
System Function Notation
In DSP, filters are described by their system function, the z-transform of the impulse response. In this notation (as in Oppenheim and Shafer, for example), we have:
Related
Published at DZone with permission of John Cook, DZone MVB. See the original article here.
Opinions expressed by DZone contributors are their own.

Comments