What Is Breadth-First Search?

Why Should I Care?

A lot of algorithms are implemented for you as part of your chosen language. That means that they are interesting to learn about, but you'll rarely write them yourself.

Graph traversal algorithms are different. We use graphs all the time, from linking related products in an e-commerce application to mapping relationships between people in a social network.

Searching a graph is something that is not only useful in theory but that you will almost certainly need to do in practice too.

In 5 Minutes or Less:

Here's a graph data structure:

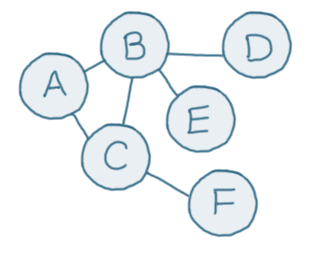
The "nodes" in the graph (A-F) are called "vertices." Each vertex is connected to one or more others with "edges," which are the lines between the nodes. However, a graph is only useful if we can do something with it. We might want to find out whether a certain element is stored in our graph, or how many "hops" it takes to get between two elements.

These kinds of problems are called "graph traversal," and Breadth-First Search (or BFS) is one algorithm to do this. Let's take a look.

How Breadth-First Search Works

In the last issue, we looked at the "queue" data structure.

You'll remember that it's a "First In, First Out" data structure: the first element to be added is the first element to be processed (or "dequeued"). If you're last in the queue, you'll be processed last:

We'll use a queue to implement Breadth-First Search (BFS).

This is the BFS algorithm:

• Pull the next "vertex" from the queue.
• For each vertex connected to this one (that we haven't already visited), mark it as "visited" and add it to the queue.
• Repeat until the queue is empty.

By doing so, we're radiating outwards from our starting point, visiting all of the nodes directly connected to the starting point first. Then, visiting all of the nodes connected to those, etc.

This will make more sense as we work through it.

Implementing BFS

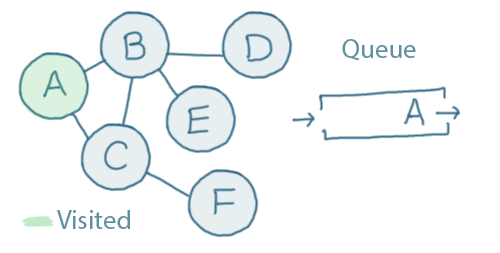
We start by picking a place to start, we'll choose A.

So, the first step is to add A to the queue and mark it as "visited":

You'll remember that the BFS algorithm requires us to repeat the following steps until the queue is empty:

• Pull the next "vertex" from the queue.
• For each vertex connected to this one (that we haven't already visited), mark it as "visited" and add it to the queue.

A is the first (and only) element in the queue.

A is connected to both B and C. We haven't visited either of those, so we'll add them to the queue and mark them as visited:

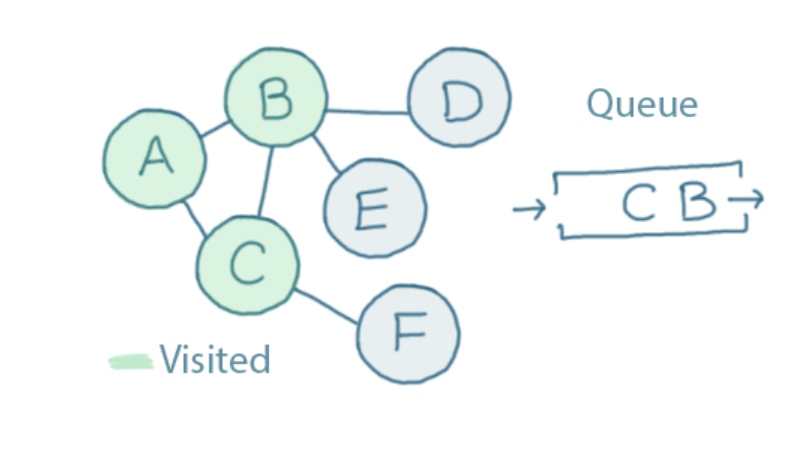
Now, we repeat the same thing again.

B is next in the queue.

B is connected to A, C, D and E. We've already visited A and C, so we only queue up D and E (and mark them as visited):

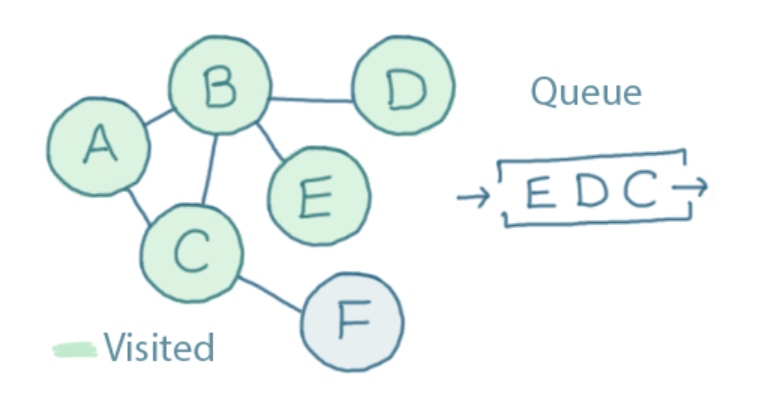
You can probably see where this is going.

Next, we dequeue C. It is connected to A, B and F. The only one we haven't already visited is F, so we add that to the queue and mark it as "visited":

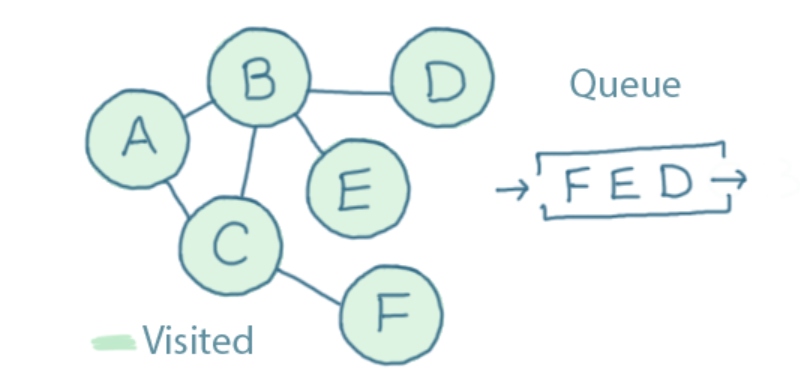
We now have F, E and D left in the queue. We'll dequeue each of them in turn, looking for any connected vertices that we haven't visited yet, but we won't find any.

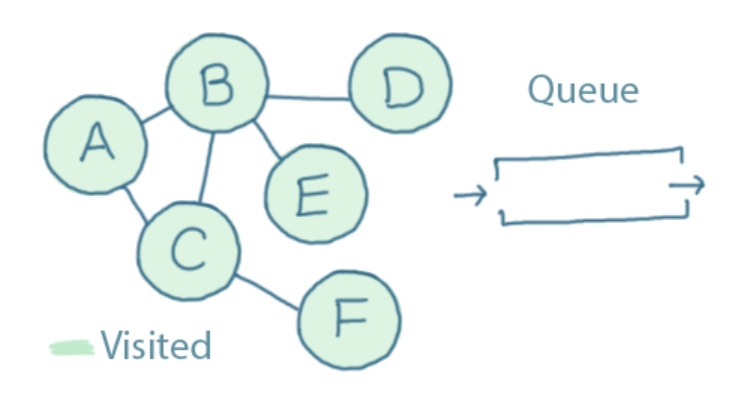
After we've checked each of those, the queue is empty and we're done. We've visited every node:

Applications of BFS

This is all very well, but what would we use it for?

Suppose we're building a social network like LinkedIn. The "graph" in this case would be the map of all connections between people. If we wanted to find out whether Bob knew Jennie through one or more mutual friends, BFS would be a great choice.

We'd start at Bob, and radiate outwards until we found Jennie (or until we were far enough away from Bob that we've given up); or, the graph could be a map of a subway, and the problem of how many mutual friends between Bob and Jennie could instead be, "How many changes does it take to get between two stations?".

Once you learn about graphs and algorithms like Breadth-First Search, a lot of problems start to look like these.

Want to Know More?

Check out these links:

• Applications of graphs in general (not specific to BFS)
• Another description of BFS
• Exploring the time complexity of BFS