A Simple Simulation of Custom Physical Interaction With Python and Matplotlib

Hello!

Here, we are going to simulate some vector field (for instance, an electromagnetic field) in an N-d space.

Our plan is:

1. To define our theoretical base (like arrays in numpy).
2. To define the mechanism of point particles and interaction fields.
3. To visualize an electric field.
4. To visualize the movement of particles in an electromagnetic field.

You may also like: Vector Based Languages.

Theoretical Base

Vector

The basic element of any physical scene is a Vector. What do we need? Arithmetic operations on a vector, distance, module, and a couple of technical things. The vector we will inherit from List. This is how its initialization looks:

class Vector(list):
    def __init__(self, *el):
        for e in el:
            self.append(e)

Now, we can create a vector with

v = Vector(1, 2, 3)

Let's set the arithmetic operation addition:

class Vector(list):
...
    def __add__(self, other):
        if type(other) is Vector:
            assert len(self) == len(other), "Error 0"
            r = Vector()
            for i in range(len(self)):
                r.append(self[i] + other[i])
            return r
        else:
            other = Vector.emptyvec(lens=len(self), n=other)
            return self + other

Result:

v1 = Vector(1, 2, 3)
v2 = Vector(2, 57, 23.2)
v1 + v2
>>> [3, 59, 26.2]

We similarly define all the arithmetic operations (the full code of the vector is at the end). Now, we need a distance function. I could simply make dist (v1, v2) — but this is not beautiful, so we will redefine the % operator:

class Vector(list):
...
    def __mod__(self, other):
        return sum((self - other) ** 2) ** 0.5

Result:

v1 = Vector(1, 2, 3)
v2 = Vector(2, 57, 23.2)
v1 % v2
>>> 58.60068258988115

We also need a couple of methods for faster vector generation and beautiful output. There is nothing tricky here, so here is the entire code of the Vector class.

A Particle

Here, in theory, everything is simple — the point has coordinates, speed, and acceleration. In addition, it has mass and a set of custom parameters (for example, for an electromagnetic field, you can set charge).

Initialization will be the following:

class Point:
    def __init__(self, coords, mass=1.0, q=1.0 speed=None, **properties):
        self.coords = coords
        if speed is None:
            self.speed = Vector(*[0 for i in range(len(coords))])
        else:
            self.speed = speed
        self.acc = Vector(*[0 for i in range(len(coords))])
        self.mass = mass
        self.__params__ = ["coords", "speed", "acc", "q"] + list(properties.keys())
        self.q = q
        for prop in properties:
            setattr(self, prop, properties[prop])

To move, immobilize and accelerate our point, we will write the following methods:

class Point:
...
    def move(self, dt):
        self.coords = self.coords + self.speed * dt

    def accelerate(self, dt):
        self.speed = self.speed + self.acc * dt

    def accinc(self, force):  # Considering exerted force the point obtains acceleration
        self.acc = self.acc + force / self.mass

    def clean_acc(self):
        self.acc = self.acc * 0

Well done, the point itself is done.

The code for Point.

Interaction Field

We call a field of interaction an object that includes a set of all particles from space and exerts force on them. We will consider a special case of our universe, so we will have one custom interaction (of course, this is easy to expand). Declare the constructor and add a point:

class InteractionField:
    def __init__(self, F):  # F - is a custom force, F(p1, p2, r), p1, p2 - points, r - distance inbetween
        self.points = []
        self.F = F

    def append(self, *args, **kwargs):
        self.points.append(Point(*args, **kwargs))

Now, the fun part is to declare a function that returns “tension” at that point. Although this concept refers to electromagnetic interaction, in our case, it is some abstract vector, along which we will move the point. In this case, we will have the property of the point q, in the particular case — the charge of the point (in general — whatever we want, even the vector). So, what is tension at point C? Something like this: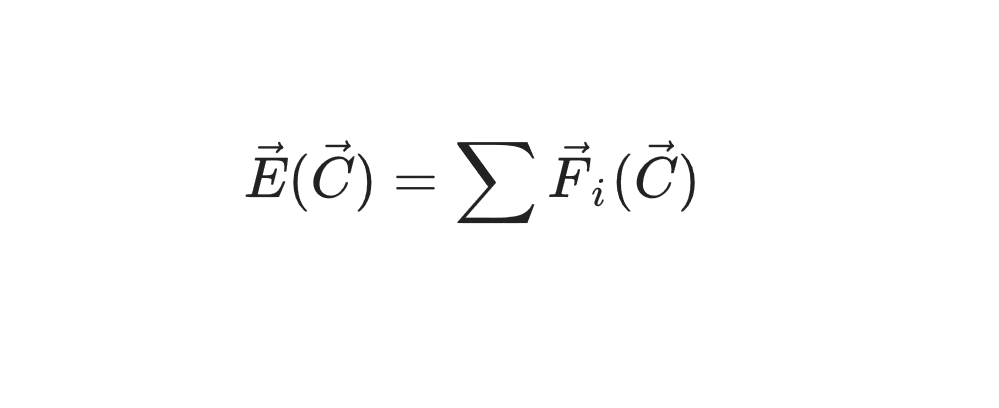

Electric intensity in point C is equal to the sum of the forces of all material points acting on some unit point.

class InteractionField:
...
    def intensity(self, coord):
        proj = Vector(*[0 for i in range(coord.dim())])
        single_point = Point(Vector(), mass=1.0, q=1.0)  # That's our "Single point"
        for p in self.points:
            if coord % p.coords < 10 ** (-10):  # Check whether we compare coord with a point P where P.coords = coord
                continue
            d = p.coords % coord
            fmod = self.F(single_point, p, d) * (-1)    
            proj = proj + (coord - p.coords) / d * fmod 
        return proj

At this point, you can already visualize a vector field, but we will do it at the end. Now, let's take a step in our interaction.

class InteractionField:
...
    def step(self, dt):
        self.clean_acc()
        for p in self.points:
            p.accinc(self.intensity(p.coords) * p.q)
            p.accelerate(dt)
            p.move(dt)

For each point, we determine the intensity in these coordinates and then determine the final force on this particle:

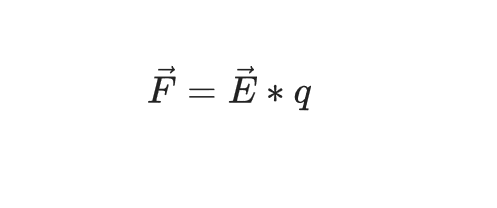
The final code for InteractionField.

Particle Movement and Vector Field Visualization

We finally reached the most interesting part. Let's start with ...

Modeling the motion of particles in an electromagnetic field

u = InteractionField(lambda p1, p2, r: 300000 * -p1.q * p2.q / (r ** 2 + 0.1))
for i in range(3):
    u.append(Vector.randvec(2) * 10, q=random.random() - 0.5)

Actually, the coefficient k should be equal to some kind of billions (9 * 10 ^ (- 9)), but since it will be quenched by the time t -> 0, it is easier to make both of them normal numbers. Therefore, in our physics k = 300,000.

Next, we add ten points (2-dimensional space) with coordinates from 0 to 10 along each axis. Also, we give each point a charge from -0.25 to 0.25. Then, we run through a loop and draw points according to their coordinates (and traces):

X, Y = [], []
for i in range(130):
    u.step(0.0006)
    xd, yd = zip(*u.gather_coords())
    X.extend(xd)
    Y.extend(yd)
plt.figure(figsize=[8, 8])
plt.scatter(X, Y)
plt.scatter(*zip(*u.gather_coords()), color="orange")
plt.show()

What should have happened is:

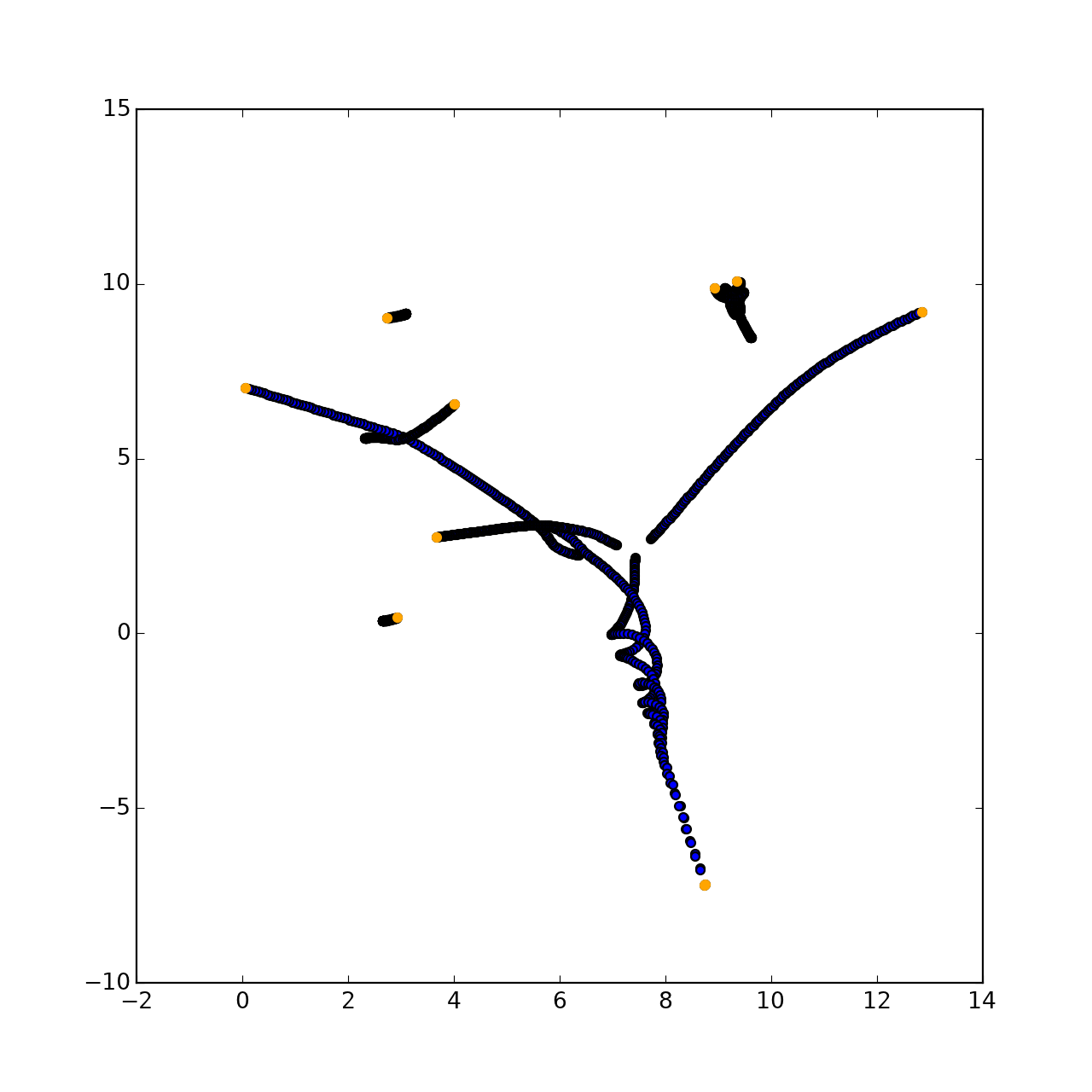
In fact, the plot will be completely random because the trajectory of each point is currently (in 2019) unpredictable.

Vector Field Visualization

We need to go through the coordinates by some step and draw a vector in each of them in the right direction.

fig = plt.figure(figsize=[5, 5])
res = []
STEP = 0.3
for x in np.arange(0, 10, STEP):
    for y in np.arange(0, 10, STEP):
        inten = u.intensity(Vector(x, y))
        F = inten.mod()
        inten /= inten.mod() * 4  # длина нашей палочки фиксирована
        res.append(([x - inten[0] / 2, x + inten[0] / 2], [y - inten[1] / 2, y + inten[1] / 2], F))
for r in res:
    plt.plot(r[0], r[1], color=(sigm(r[2]), 0.1, 0.8 * (1 - sigm(r[2])))) # Цвет по хитрой формуле чтобы добиться градиента

plt.show()

You should have gotten something like this:

You can lengthen the vectors themselves, replace * 4 with * 1.5:

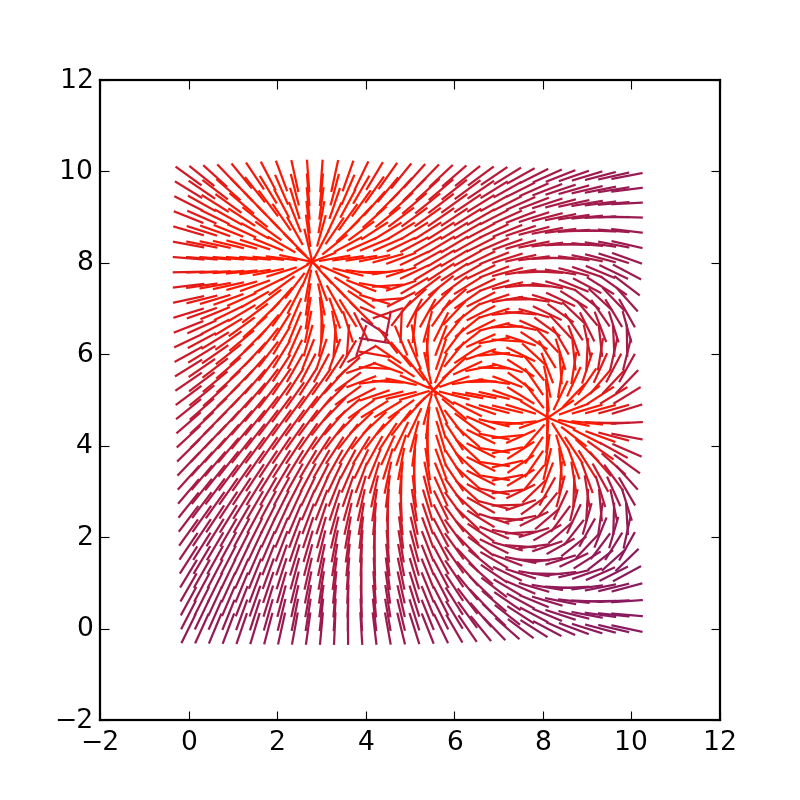
Change dimensionality

Let's create a five-dimensional space with 200 points and an interaction that is not dependent on the square of the distance, but on the 4th degree.

u = InteractionField(lambda p1, p2, r: 300000 * -p1.q * p2.q / (r ** 4 + 0.1))
for i in range(200):
    u.append(Vector.randvec(5) * 10, q=random.random() - 0.5)

Now, all coordinates, speeds, etc. are defined in five dimensions. Now, let's model something:

velmod = 0
velocities = []
for i in range(100):
    u.step(0.0005)
    velmod = sum([p.speed.mod() for p in u.points])   # Adding sum of modules of all the velocities
    velocities.append(velmod)
plt.plot(velocities)
plt.show()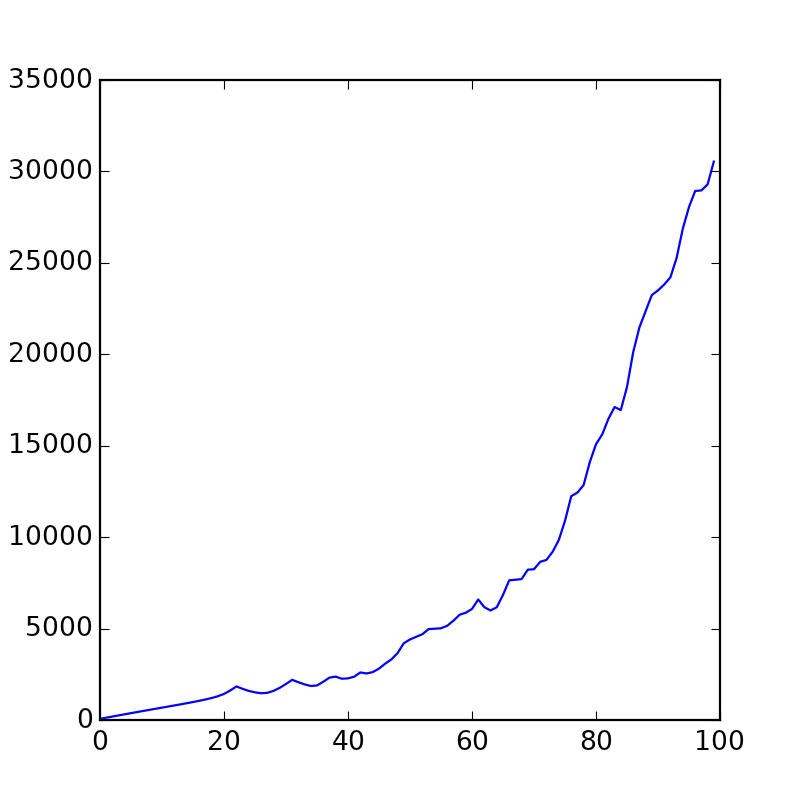

This is a graph of the sum of all speeds at any given time. As you can see, over time they are slowly accelerating.

Well, that was a short instruction on how to simply simulate elementary physical stuff, thank you for your attention.

Video how it works.

Interaction field.

Point.

Vector.

Further Reading

• Yet Another Android Snake With Kivy, Python.