Demystifying Big O Notation

Understanding how efficient your code is just by looking at it can be tricky. Thankfully, the brilliant minds before us have come up with a neat trick: Big O notation. This fancy little concept helps us measure how much time and space an algorithm will consume based on its input. 

So, why should we care? Well, as engineers, our job boils down to two things: solving problems that have never been solved before or solving problems that have been solved but in a more efficient way. Knowing Big O helps us make smarter decisions about which algorithms to use. It’s like having a cheat sheet for predicting how much time and memory your code will need, depending on the input size. Sounds good, right? Let’s break it down with a simple example: O(n), also known as linear time complexity.

O(n): A Linear Approach

Take a look at this function:

const arr = [1, 3, 5, 5, 4, 6, 12, ...];

const addAllArrayElements = (arr) =>{

  let sum = 0;

  for(let i=0; i < arr.length; i++){

    sum += arr[i];

  }

  return sum;

}

Here, we have a simple function that takes an array of numbers and adds them all together. Now, let’s talk Big O. The for loop in this example runs once for each element in the array, which means the time taken grows directly with the size of the array. If there are n elements in the array, the function runs n times. Hence, we call this O(n) — linear time complexity.

Sure, you might point out that adding a value to the sum variable takes some time, too. And you’re right! But in Big O terms, we ignore those small details (like constants) because they don’t significantly change how the function behaves as the input size grows.

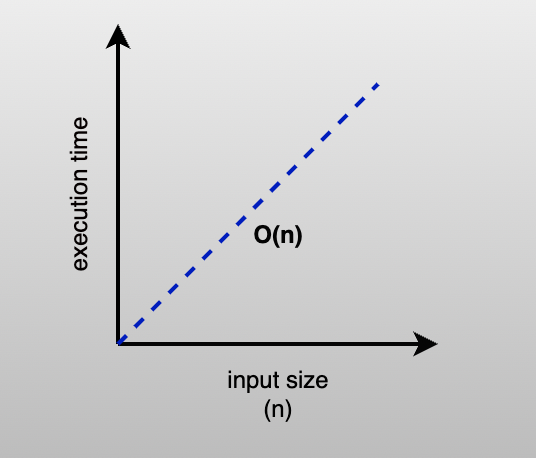
As you can see, the execution time increases linearly with the input size. This is great when working with small arrays, but if the input grows, you might want to rethink your approach. 

The Power of Loops

Let’s move on to a slightly more complicated example. The key to recognizing Big O complexity lies in loops — they’re the most reliable indicator of how an algorithm scales with input size. Here's a new example:

const arr = [1, 3, 5, 5, 4, 6, 12, ...];

const addAllArrayElementsTwice = (arr) =>{

  let sum = 0;

  for(let i=0; i < arr.length; i++){

    sum += arr[i];

  }

  for(let i=0; i < arr.length; i++){

    sum += arr[i];

  }

  return sum;

}

In this case, we’re looping through the array twice. One loop adds all the elements, and the second one adds them all over again. So, what’s the time complexity here? O(2n). But before you get excited thinking you’ve figured it out — hold up! We don’t care about constants in Big O. That means O(2n) is effectively just O(n).

Here’s a good tip: when analyzing an algorithm, think of the process as a whole. Even though we have two loops, it’s still linear, so the time complexity stays O(n).

Nested Loops: O(n²)

Now, let’s crank things up a bit. What happens if we add another nested loop inside the first one?

const arr = [1, 3, 5, 5, 4, 6, 12, ...];

const addAllArrayElementsTwice = (arr) =>{

  let sum = 0;

  for(let i=0; i < arr.length; i++){

    sum += arr[i];

    for(let j=0; j < arr.length; j++){

      sum += arr[j];

    }

  }

  return sum;

}

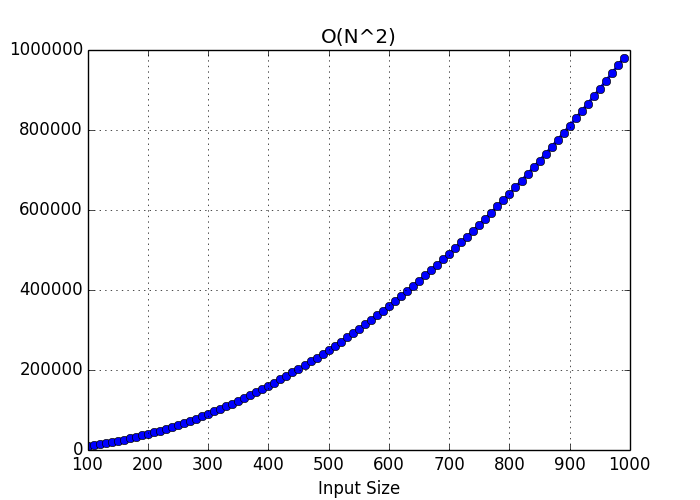
Here, the function does something interesting: for each element in the array, it loops through the array again and adds every element to the sum. This gives us O(n²) time complexity, also known as quadratic time complexity. The outer loop runs n times, and for each outer loop iteration, the inner loop runs n times. So, the total work done grows quadratically with the size of the input.

Want to make it worse? Add another nested loop, and you’re looking at O(n³). The more nested loops, the higher the exponent.

Other Common Time Complexities

There are plenty of other important complexities you’ll encounter as you dive deeper into algorithms. Some of the most common include:

• O(log n): This is usually seen in algorithms that divide the input in half at each step, like binary search.
• O(n log n): You’ll often see this complexity in efficient sorting algorithms like Merge Sort or Quick Sort, where the input is divided into smaller chunks (log n) and then processed linearly (n).

Here's a quick reference to visualize the different complexities:

Wrapping It Up

Big O is a powerful tool for understanding how an algorithm behaves as the input grows. It allows us to make smarter decisions about which algorithms to use based on how they perform with large datasets. Whether it’s O(n), O(n²), or something more complex, knowing the time complexity can help us choose the right approach for solving problems.

Keep an eye on loops and nesting, and soon you’ll start seeing how Big O helps you predict algorithm performance with just a quick glance and make sure to explore more on your own when it comes to Big O Notation.