Essential Math to Master AI and Quantum
Learn the essential subset of mathematical concepts to understand the underpinnings of artificial intelligence and quantum computing.
Join the DZone community and get the full member experience.
Join For FreeThe essential mathematics for both Artificial intelligence (AI) and quantum computing are foundational to understanding and advancing these cutting-edge fields. In AI, concepts like linear algebra, calculus, probability theory, and optimization are pivotal for modeling data, training machine learning algorithms, and making predictions.
Similarly, in quantum computing, these mathematical pillars are indispensable for representing quantum states, designing quantum algorithms, and analyzing quantum phenomena. Whether it's optimizing neural networks or harnessing the power of quantum superposition, a solid grasp of these mathematical principles is crucial for pushing the boundaries of artificial intelligence and quantum computing alike.
Complex Numbers
Complex numbers, which consist of a real and imaginary part (a+ib), and complex arithmetic and functions are fundamental to quantum mechanics. They allow for the representation of quantum states and the mathematical operations performed on them. In AI, complex numbers have also found applications in areas like neural networks and signal processing.
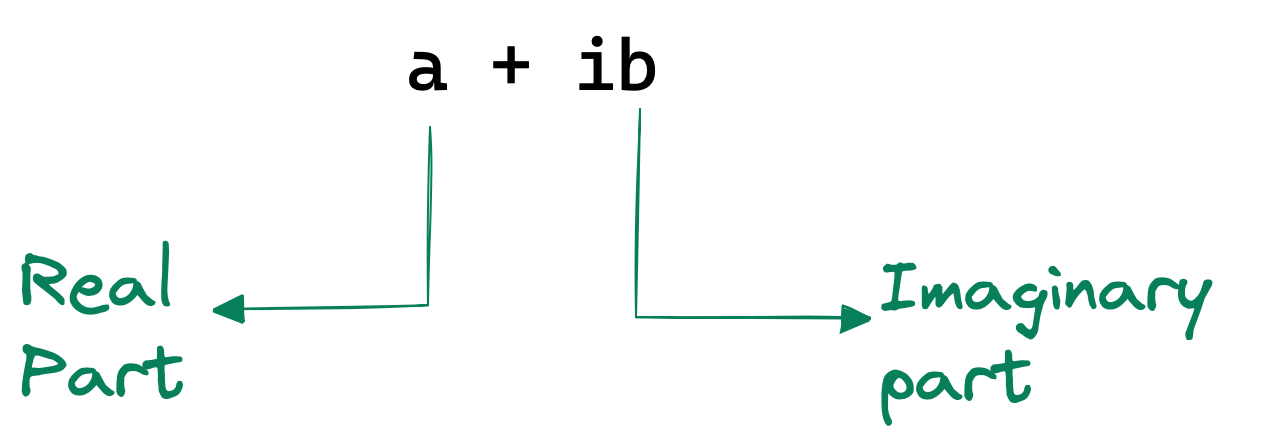
A complex number
Linear Algebra
Linear algebra, including concepts like vectors, matrices, linear transformations, and eigenvalues/eigenvectors, is crucial for both quantum computing and many AI techniques. It provides the mathematical framework for representing and manipulating the states and operators in quantum systems, as well as the data structures and algorithms used in AI.
Calculus and Optimization
Calculus and optimization are crucial for training and tuning AI models, as well as for understanding the dynamics of quantum systems. The key concepts that need basic understanding are differentiation and integration, gradient-based optimization techniques, and variational methods.
Additionally, a good understanding of convex optimization is an add-on in the context of optimization algorithms and loss minimization. Refer to Convex Optimization by Boyd and Vandenberghe.
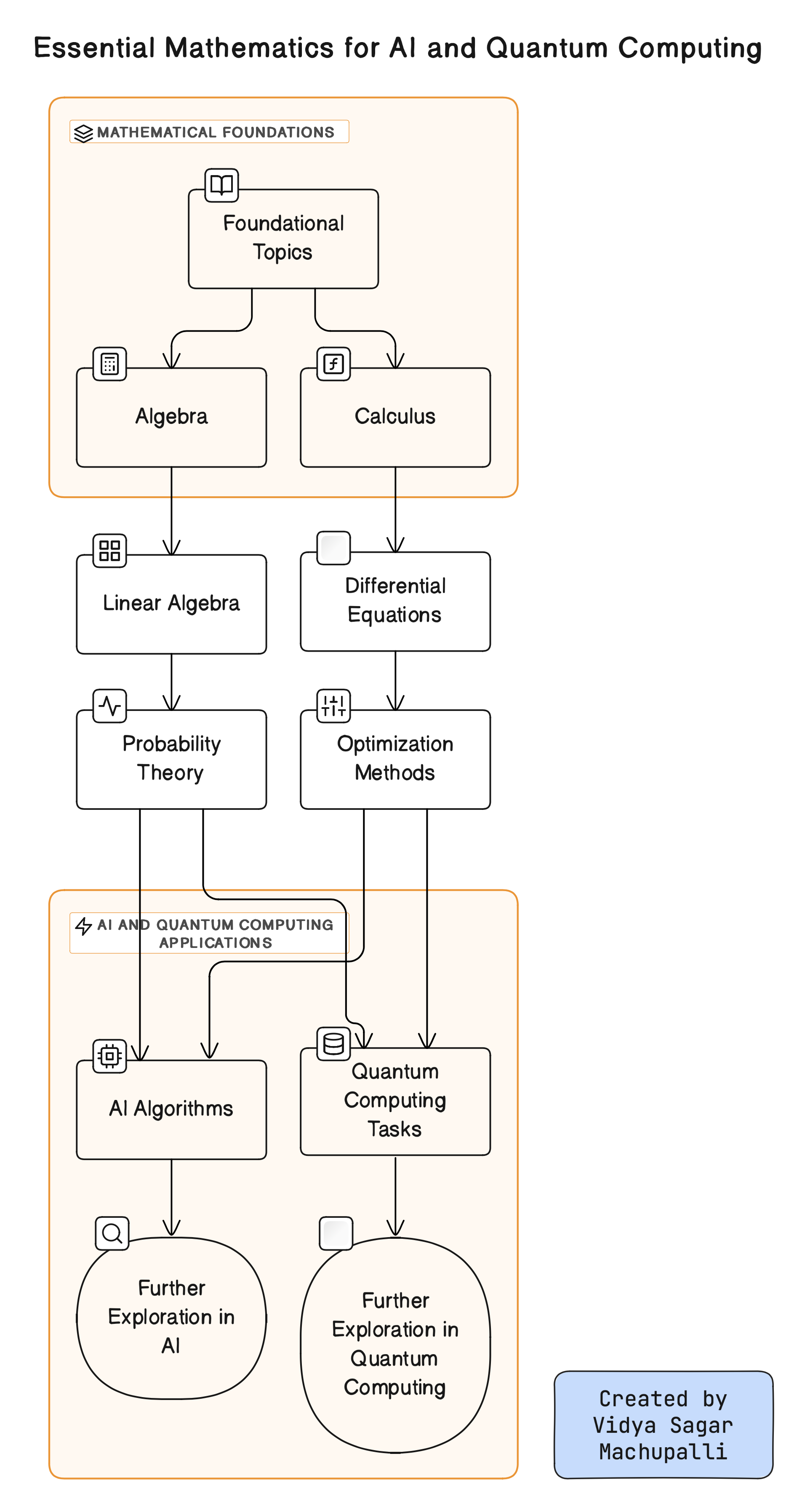
Mathematics for AI and Quantum
Hilbert Spaces
Quantum mechanics utilizes the mathematical structure of Hilbert spaces, which generalize the concepts of vectors and linear algebra to infinite dimensions. This allows for the representation of quantum states as vectors in a Hilbert space. Some AI models, such as those based on kernel methods, also make use of Hilbert space structures.
Probability and Statistics
Both quantum computing and AI rely heavily on probability theory and statistical methods. Quantum mechanics describes the probabilistic nature of measurements, while many AI algorithms, like Bayesian networks and reinforcement learning, are built on probabilistic foundations.
Group Theory and Representation Theory
Symmetry groups, unitary transformations, and irreducible representations are advanced mathematical concepts that are important for understanding the underlying structure of quantum systems and some quantum algorithms.
Conclusion
While the depth of understanding required may vary, a solid grasp of these core mathematical areas is essential for both advancing AI, including deep learning, and developing quantum computing technologies. The essential mathematics for both AI and quantum computing share several key concepts. Linear algebra serves as a cornerstone, enabling the representation of data and quantum states through vectors and matrices. Probability theory underpins both fields, facilitating the understanding of uncertainty in AI models and the probabilistic nature of quantum phenomena. Optimization techniques play a vital role in training machine learning models and optimizing quantum algorithms.
Additionally, concepts from calculus provide the mathematical framework for gradient-based optimization and understanding quantum dynamics. Together, these mathematical foundations form the basis for advancing research and innovation in both AI and quantum computing domains.
Opinions expressed by DZone contributors are their own.

Comments