InOrder Traversal Algorithm in Java

Hello guys, recently one of my readers was asked about how do you print all nodes of a binary search tree in sorted order during a telephonic Java interview. Unfortunately, he didn’t know that InOrder traversal can be used to print nodes in sorted order and he asked me after the interview.

In the past, I have share best data structure courses and data structure interview questions and today, I will teach you about interesting and useful binary tree algorithms called InOrer traversal. We will also see an implementation using the Java programming language. 

What Is InOrder Traversal Algorithm?

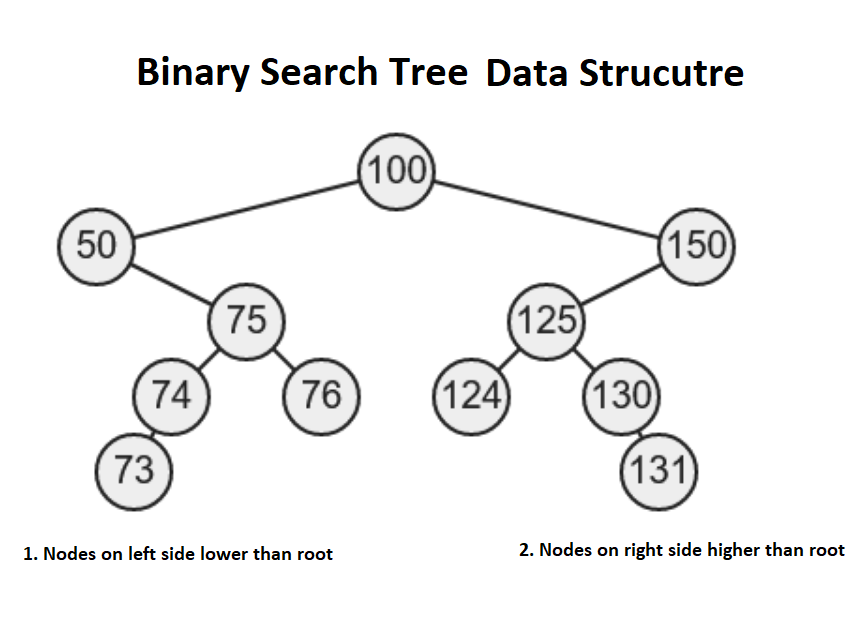
The InOrder traversal is one of the three popular ways to traverse a binary tree data structure, the other two being the preOrder and postOrder. During the in-order traversal algorithm, the left subtree is explored first, followed by root, and finally nodes on the right subtree.

You start traversal from the root≤ then go to the left node, and then again go to the left node until you reach a leaf node. At that point in time, you print the value of the node or mark it visited and moves to the right subtree. Continuing the same algorithm until all nodes of the binary tree are visited. 

The InOrder traversal is also known as the left-node-right or left-root-right traversal or LNR traversal algorithm.

Similar to the preOrder algorithm, it is also a depth-first algorithm because it explores the depth of a binary tree before exploring siblings. Since it is one of the fundamental binary tree algorithms, it’s quite popular in programming interviews.

These traversal algorithms are also the basis to learn more advanced binary tree algorithms, hence every programmer should learn, understand, and know how to implement in-order and other traversal algorithms. Btw, if you are preparing for coding interviews then I highly recommend you to check out Andrei Neagoie's Master the Coding Interview: Data Structures + Algorithms course, it's truly the gem and you will learn a lot. 

The easiest way to implement the inOrder traversal algorithm in Java or any programming language is by using recursion. Since the binary tree is a recursive data structure, recursion is the natural choice for solving a tree-based problem. The inOrder() the method in the BinaryTree class implements the logic to traverse a binary tree using recursion.

From the Interview point of view, InOrder traversal is extremely important because it also prints nodes of a binary search tree in the sorted order but only if a given tree is a binary search tree. 

If you remember, in BST, the value of nodes in the left subtree is lower than the root, and the values of nodes on the right subtree are higher than the root. The InOrder traversal literally means IN order, I mean, nodes are printed in the order or sorted order.

Btw, even though these three algorithms (pre-order, in-order, and post-order) are popular binary tree traversal algorithms but they are not the only ones. You also have other breadth-first ways to traverse a binary tree, like level order traversal.

The Recursive Algorithm to Implement InOrder Traversal of a Binary Tree

The recursive algorithm of InOrder traversal is very simple. You just need to call the inOrder() method of BinaryTree class in the order you want to visit the tree. What is most important is to include the base case, which is key to any recursive algorithm.

For example, in this problem, the base case is you reach the leaf node and there is no more node to explore, at that point of time recursion starts to wind down. Here are the exact steps to traverse the binary tree using InOrder traversal:

1. Visit left node
2. Print value of the root
3. Visit the right node and here is the sample code to implement this algorithm using recursion in Java:

xxxxxxxxxx

private void inOrder(TreeNode node) {

    if (node == null) {

      return;

    }

    inOrder(node.left);

    System.out.printf("%s ", node.data);

    inOrder(node.right);

}

Similar to the preOrder() method in the last example, there is another inOrder() the method which exposes inOrder traversal to the public and calls this private method which actually performs the InOrder traversal.

This is the standard way to write a recursive method which takes input, it makes it easier for a client to call the method.

xxxxxxxxxx

public void inOrder() {

    inOrder(root);

}

You can see that we start with root and then recursive call the inOrder() method with node.left, which means we are going down on the left subtree until we hit node == null, which means the last node was a leaf node.

At this point in time, the inOrder() method will return and execute the next line, which prints the node.data. After that, its again a recursive inOrder() call with node.right, which will initiate the same process again.

Inorder traversal of a Binary Tree in Java

Here is our complete solution to the inorder traversal algorithm in Java. This program uses a recursive algorithm to print the value of all nodes of a binary tree using InOrder traversal.

As I have told you before, during the in-order traversal value of the left subtree is printed first, followed by the root and right subtree. 

xxxxxxxxxx

import java.util.Stack;

/*

 * Java Program to traverse a binary search tree

 * using inorder traversal without recursion 

 * and print all nodes in sorted order

 * In InOrder traversal first left node is visited, followed by root

 * and right node.

 *

 * input:

 *      40

 *     /\

 *    20   50

 *   / \    \

 *  10  30   60

 * /   /  \

 * 5  67  78

 *

 * output: 5 10 20 30 40 50 60 67 78

 */

public class Main {

  public static void main(String[] args) throws Exception {

    // construct the binary tree given in question

    BinaryTree bt = BinaryTree.create();

    // traversing binary tree using InOrder traversal using recursion

    System.out

        .println("printing nodes of binary tree on InOrder using recursion");

    bt.inOrder();

  }

}

class BinaryTree {

  static class TreeNode {

    String data;

    TreeNode left, right;

    TreeNode(String value) {

      this.data = value;

      left = right = null;

    }

  }

  // root of binary tree

  TreeNode root;

  /**

   * traverse the binary tree on InOrder traversal algorithm

   */

  public void inOrder() {

    inOrder(root);

  }

  private void inOrder(TreeNode node) {

    if (node == null) {

      return;

    }

    inOrder(node.left);

    System.out.printf("%s ", node.data);

    inOrder(node.right);

  }

  /**

   * Java method to create binary tree with test data

   *

   * @return a sample binary tree for testing

   */

  public static BinaryTree create() {

    BinaryTree tree = new BinaryTree();

    TreeNode root = new TreeNode("40");

    tree.root = root;

    tree.root.left = new TreeNode("20");

    tree.root.left.left = new TreeNode("10");

    tree.root.left.left.left = new TreeNode("5");

    tree.root.left.right = new TreeNode("30");

    tree.root.right = new TreeNode("50");

    tree.root.right.right = new TreeNode("60");

    tree.root.left.right.left = new TreeNode("67");

    tree.root.left.right.right = new TreeNode("78");

    return tree;

  }

}

Output
 printing nodes of the binary tree on InOrder using recursion
 5 10 20 30 67 78 40 50 60

That’s all about how to implement inOrder traversal of a binary tree in Java using recursion. You can see the code is pretty much similar to the preOrder traversal with the only difference in the order we recursive call the method. In this case, we call inOrder(node.left) first and then print the value of the node.

It’s worth remembering that in order traversal is a depth-first algorithm and prints tree node in sorted order if the given binary tree is a binary search tree.

In the next part of this article, I’ll share inOrder traversal without recursion, meanwhile, you can try practicing following data structure and binary tree problems.

If you have any suggestions to make this algorithm better, feel free to suggest. The interviewer loves people who come up with their own algorithm or give some touch to popular algorithms.