IoU Score and Its Variants for Deep Learning
A deep dive into the hugely popular IoU score, its limitations, and recent improvements with Generalized IoU and Signed IoU.
Join the DZone community and get the full member experience.
Join For FreeScores and metrics in machine learning are used to evaluate the performance of a model on a given dataset. These provide a way to understand how a model is performing and also compare different models and choose the one that performs the best.
In this article, we will focus on the IoU score, which stands for Intersection over Union. IoU is a widely used metric in the field of object detection, where the goal is to locate and classify objects in images or videos. We'll also identify limitations and solutions.

Object Detection
In Machine Learning (well, Deep Learning, here), an Object Detection task refers to inferring a bounding box around an object of interest. This can be paired with a classification task to identify what object is being detected, but that is not of concern to us today. An object detection model is trained using some ground truth bounding boxes. This ground truth could be annotated by a human labeler or by using auto-labeling mechanisms.
IoU Score
The model training needs some signal to identify how to update the model (this is called the forward pass and backpropagation). In the object detection space, Intersection Over Union (IoU) score is the most commonly used metric. IoU is also referred to as the Jaccard index or Jaccard similarity coefficient, which measures how similar two sets are.
IoU measures the overlap between the predicted bounding box and the ground truth bounding box. It is calculated as the Ratio of the Intersection of the two bounding boxes to the Union of the two bounding boxes.
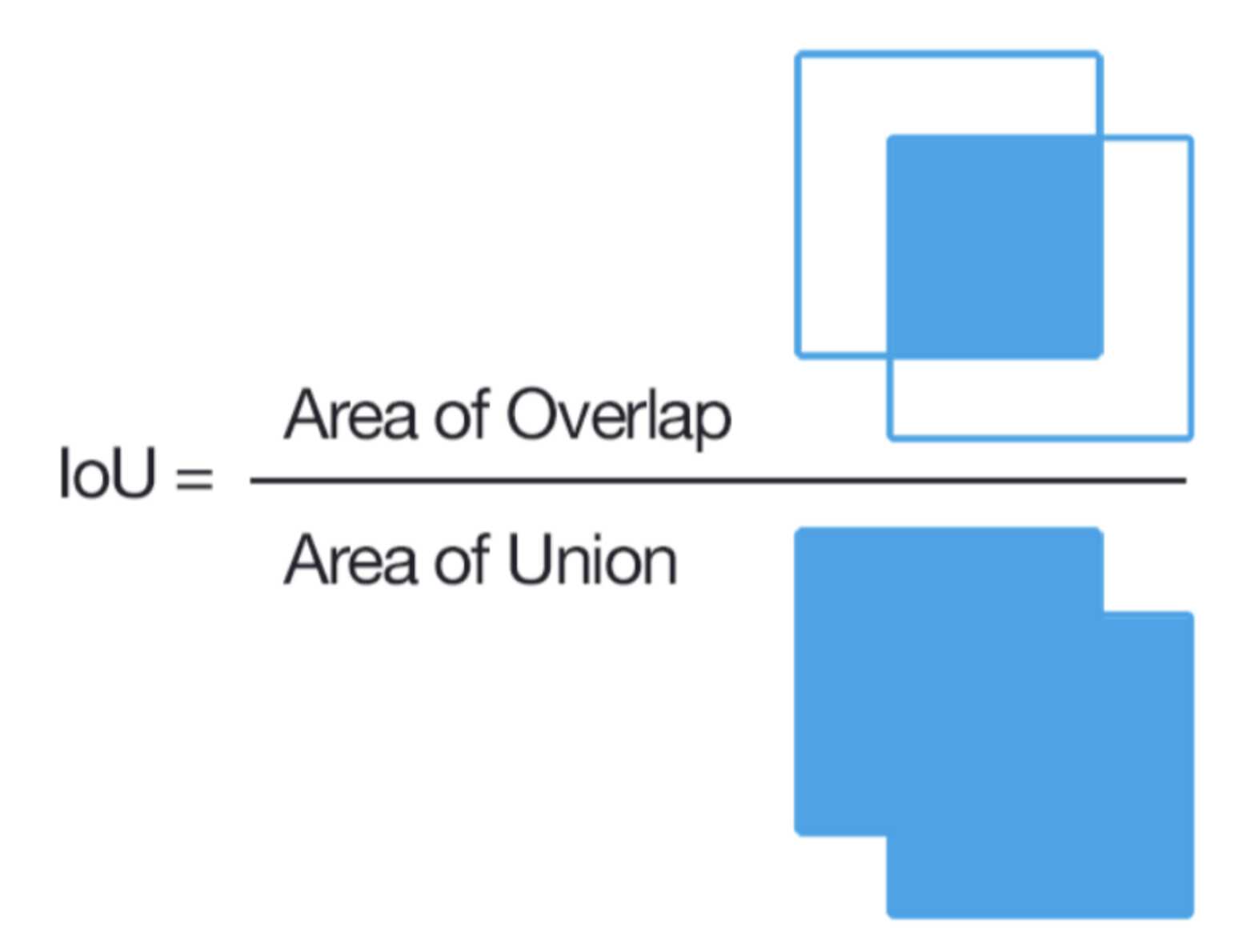
IoU is used as the evaluation metric for object detection tasks because it takes into account both the location and the size of the bounding box. A high IoU score indicates that the predicted bounding box is well-aligned with the ground truth bounding box.
Important Property
The IoU score is bounded in [0, 1] (0 being no overlap and 1 being full/ complete/perfect overlap).
Implementation
While most ML/DL libraries will provide an easy-to-use implementation for IoU, it’s great to be able to do this yourself. (PS.: This also makes for a great interview question ;) )
And here is a neat little trick to solve this problem efficiently (and impress your interviewer).
Remember that we are dealing with axis-aligned rectangles here. This means the edges of the bounding boxes are aligned (parallel) with the Cartesian coordinate system of the image.
There are a few ways to represent rectangles in the Cartesian system. Note that the origin (0,0) of our Cartesian system is in the Top Left corner to make this same as OpenCV and other image processing tools. For simplicity's sake, I have chosen to use the 2-point representation: Top Left (x0, y0) and Bottom Right (x1, y1). In such a representation, obviously:
- Length along X-axis =
x1 - x0 - Length along Y-axis =
y1 - y0 Area =
(x1 - x0) * (y1 - y0)
This allows us to treat the X and Y axis as the same as each other, essentially reducing our problem to 1-D instead of 2-D. The 1-D projection of the 2D boxes on their axes looks like this:
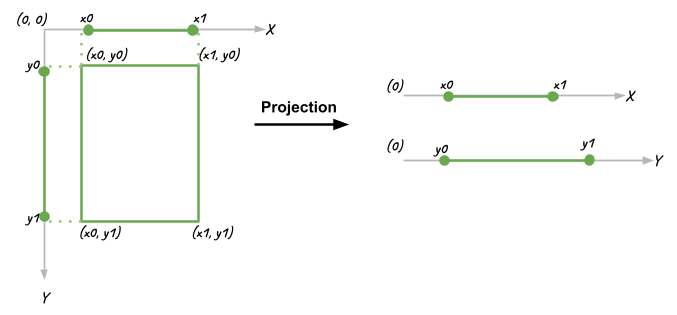
This reduces our problem from finding the intersection of 2D boxes to the overlap of 1D lines. Considerably more intuitive to think about and definitely way easier to code, with a nice reusable block of code.
Here’s how a case with actual overlap looks. In this case, both `overlap_x` and `overlap_y` are positive, non-zero values.

Another case is where there is no overlap. Here, even though overlap is calculated on the X-axis, there is no overlap on the Y-axis. The resulting area of overlap (overlap_x * overlap_y) will be 0.

Other cases are similar and are left as an exercise for the reader.
Calculating this 1-D overlap is simple. All one needs to do is find the start and the end points of this “overlapping” line
overlap = max(0, min(x1, x1) - max(x0, x0))
Here's some Python code to do that:
# Intersection Over Union
def area(length_x, length_y):
if length_x < 0 or length_y < 0:
return 0
return length_x*length_y
## Bounding Box
class Bbox:
def __init__(self, x0, y0, x1, y1):
self.x0 = x0
self.y0 = y0
self.x1 = x1
self.y1 = y1
def area(self):
return area(self.x1 - self.x0, self.y1-self.y0)
def Overlap_1D(x0_a, x1_a, x0_b, x1_b):
return max(0, min(x1_b, x1_a)-max(x0_b, x0_a))
def Intersection(a, b):
overlap_x = Overlap_1D(a.x0, a.x1, b.x0, b.x1)
overlap_y = Overlap_1D(a.y0, a.y1, b.y0, b.y1)
return area(overlap_x, overlap_y)
def IoU(a, b):
intersection = Intersection(a, b)
union = a.area() + b.area() - intersection
return intersection/ float(union)
A = Bbox(0, 0, 5, 5)
B = Bbox(1, 1, 5, 5)
print("IoU", IoU(A, B))OpenCV provides function overloads to do this too:
Union = rect1 | rect2
Intersection = rect & rect2
Hang On, Though!!
A value of one makes sense; when there is complete overlap, there is no uncertainty or improvement.
But what about when there is no overlap? Are all no-overlap cases as bad as each other?
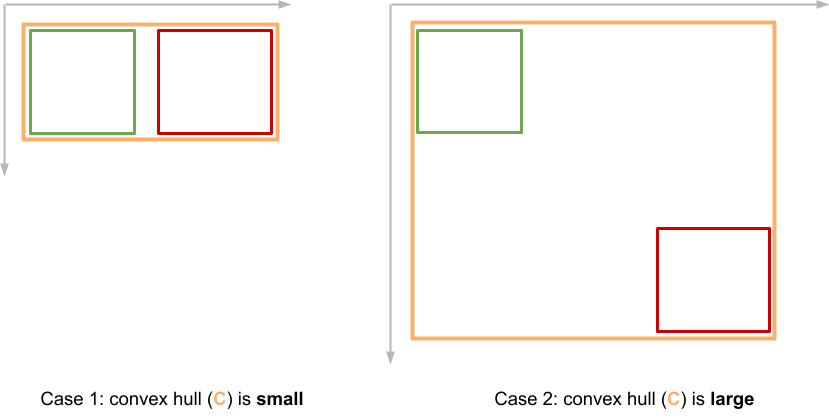
Surely, Case one (below) is a lot better than Case two. Could the IoU metric be improved to account for this?

Enter Signed IoU (SIoU) and Generalized IoU (GIoU). Both these fairly recent approaches solve the problem that the improvement in the bounding box prediction does not directly correlate with improvement in IoU score. Both `SIoU` and `GIoU` are bounded in [-1, 1]. They help with the problem of vanishing gradients where the overlap is 0.
SIoU
Assigns a sign to the area of intersection; The sign is +ve if there is overlap and -ve otherwise. In the equation below, `b` and `b^` refer to bounding boxes.
![image showing formula for signed IoU]()

GIoU
Generalized Intersection Over Union solves this problem by considering the convex hull of the 2 bounding boxes. The next figure shows an example of such a convex hull.
- It is defined as,
GIoU = IoU − ( |C\(A ∪ B)| / |C|)whereC\(A ∪ B)is the area of box A and box B removed from the convex hull. Figures are from the original paper (Generalized Intersection over Union: A Metric and A Loss for Bounding Box Regression)![Image showing convex hull for non-overlapping bounding boxes with varying distances]()
![Image showing formula for Generalized IoU]()
Where IoU is bounded at 0, GIoU continues to provide a loss signal to the network and asymptotically decays to -1.
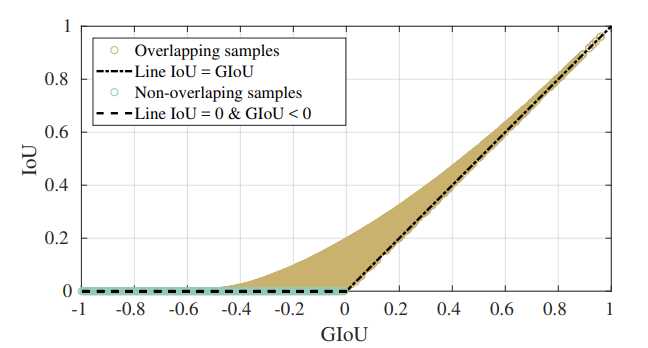
![Image showing how Generalized Io correlates with IoU]() Correlation between GIoU and IOU for overlapping (GIoU > 0) and non-overlapping (GIoU <= 0) samples.
Correlation between GIoU and IOU for overlapping (GIoU > 0) and non-overlapping (GIoU <= 0) samples.
Takeaways
- Scores and metrics are an essential part of the machine learning process, and they provide a way to evaluate the performance of a model on a given dataset.
- Each task has its specific requirements and the scores need to be chosen carefully.
- IoU is a commonly used metric in object detection, and it measures the overlap between the predicted bounding box and the ground truth bounding box.
- IoU is bounded in [0, 1], which means it can not differentiate between bounding boxes close to ground truth vs. far from the ground truth.
- If vanishing gradients for non-overlapping cases is a problem for you, consider GIoU or SIoU as a workaround.
Opinions expressed by DZone contributors are their own.



Comments