Learn the Math for Feedforward Neural Networks
If you're learning about feedforward neural networks for the first time, understanding the math behind them is a great place to start.
Join the DZone community and get the full member experience.
Join For FreeIn my last blog, we were discussing the biological motivations of the artificial neural network. This time, we will discuss the artificial neural network in practice. In ANNs, we have different layers of networks to solve a problem. How many layers required to solve certain problems is a different topic — and I will be writing a blog on that soon. However, we can still proceed to implement the network and make it learn how to solve the problem.
As programmers, we understand code better than anyone else and we can pick anything up pretty quickly. You can also learn about ANNs directly by going through the code. However, so far, I feel that knowing the math behind ANN algorithms helps more in understanding the process. So before going to the code, I will be discussing the math behind it. The image below is a feedforward network. There are several network structures in ANNs, but let’s start with this one first.
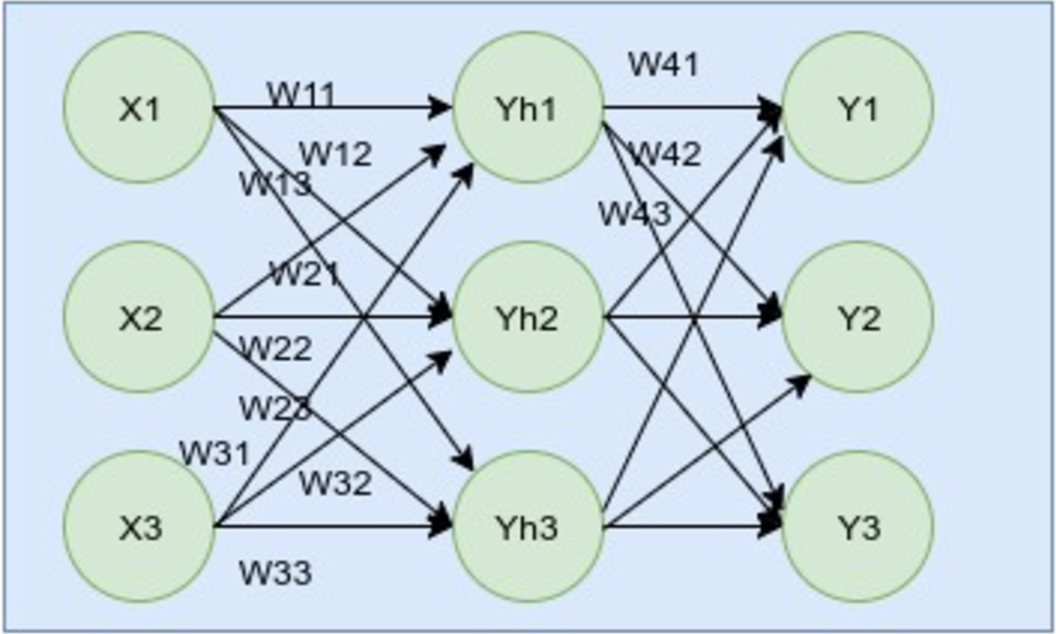
As shown in the above image, the network has three layers: input, hidden, and output. In the input layer, we have the inputs as X1, X2, ... Xn. For the middle and hidden layers, we have its outputs as Yh1, Yh2, …Yhn. For the output layer, we have the outputs as Y1, Y2, Y3. Let’s take the targeted outputs as Ŷ1, Ŷ2, … Ŷn. Similarly, we have different weights among different neurons and have named them like W11 between X1 to Yh1; W12 between X1 to Yh2; W13 between X1 to Yh3; etc. We've done it similarly for the output layer neurons, as well. An important thing to note here is that ANN works on real-valued, discrete-valued, and vector-valued inputs.
To summarize, we have the terms as below. If you’re new to neural networks, I would recommend going through them:
Inputs = X1, X2, X3
Hidden outputs = Yh1, Yh2, Yh3
Putputs = Y1, Y2, Y3
Targeted outputs = Ŷ1, Ŷ2, Ŷ3
Weights to Yh1 = W11, W12, W13
Weights to Yh2 = W21, W22, W23
Weights to Yh3 = W31, W32, W33
Weights to Y1 = W41, W42, W43
Weights to Y2 = W51, W52, W53
Weights to Y3 = W61, W62, W63
Now, we are all set and ready to implement the network mathematically. Every neuron has an activation function like f(x) = sigmoid(x). The activation function takes a parameter. Our first step is creating the input for the activation function. We do that by multiplying the weights by the input value. The formula looks like this:
XWh1 = X1.W11 + X2. W21 + X3. W31
XWh2 = X1.W12 + X2. W22 + X3. W32
XWh3 = X1.W13 + X2. W23 + X3. W33
The outputs that the hidden layers release are:
Yh1 = sigmoid(XWh1)
Yh2 = sigmoid(XWh2)
Yh3 = sigmoid(XWh3)
The outputs from the hidden layer become the input for the output layer and are multiplied by the weights for the output layer. Therefore, the multiplication is like this:
YhWo1= Yh1.W41+Yh2.W51+Yh3.W61
YhWo2= Yh1.W42+Yh2.W52+Yh3.W62
YhWo3= Yh1.W43+Yh2.W53+Yh3.W63
The final output in the output layer is like this:
Y1 = sigmoid(YhWo1)
Y2 = sigmoid(YhWo2)
Y3 = sigmoid(YhWo3)
If you’re reading about neural networks for the first time, you might be wondering what the Sigmoid function is. Here's the formula for it:

We can take different activation functions to solve different problems using ANN. When to choose which activation function is, again, a different topic that we will try to cover in another article. But briefly, the Sigmoid function produces an S-shaped curve when put on a graph. When the input for the network is real-valued and differentiable, we use the Sigmoid function so that we can easily find the gradient out of it.

And that’s it! If we implement what we have just mentioned here, our neural network is ready. The next step is to train it. But before we go detail into how to train it, our next step is to see the implementation in Scala — which we are going to see in our next blog!
Published at DZone with permission of Pranjut Gogoi. See the original article here.
Opinions expressed by DZone contributors are their own.

Comments