Learning Big O Notation With O(n) Complexity

Big O Notation is one of those things that I was taught at university, but I never really grasped the concept. I knew enough to answer very basic questions on it, but that was about it. Nothing has changed since then as I have not used or heard any of my colleagues mention it since I started working. So, I thought I’d spend some time going back over it and write this post summarizing the basics of Big O Notation along with some code examples to help explain it.

So, what is Big O Notation? In simple terms:

• It is the relative representation of the complexity of an algorithm.
• It describes how an algorithm performs and scales.
• It describes the upper bound of the growth rate of a function and could be thought of the worst case scenario.

Now for a quick look at the syntax: O(n²).

n is the number of elements that the function receiving as inputs. So, this example is saying that for n inputs, its complexity is equal to n².

Comparison of the Common Complexities

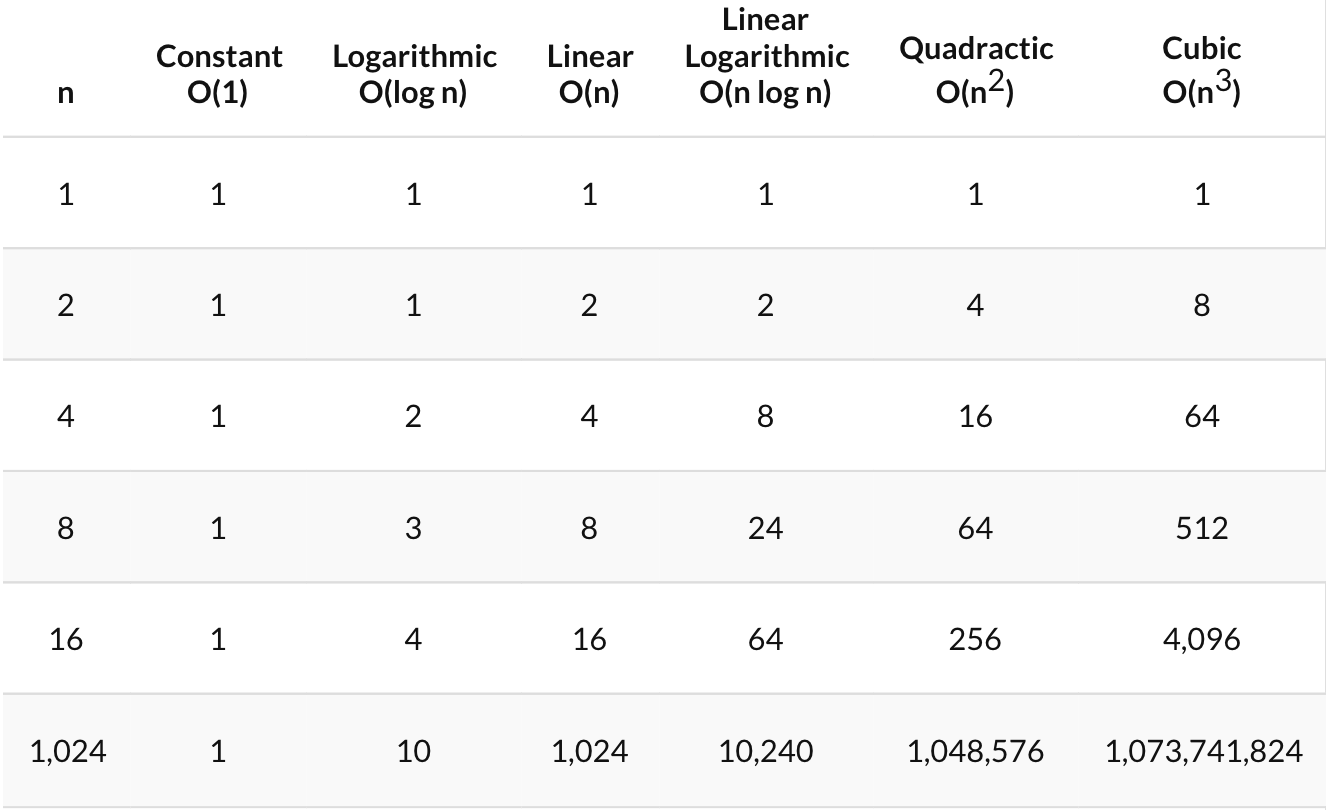
As you can see from this table, as the complexity of a function increases, the number of computations or time it takes to complete a function can rise quite significantly. Therefore, we want to keep this growth as low as possible, as performance problems might arise if the function does not scale well as inputs are increased.

Graph showing how the number of operations increases with complexity.

Some code examples should help clear things up a bit regarding how complexity affects performance. The code below is written in Java but obviously, it could be written in other languages.

O(1)

public boolean isFirstNumberEqualToOne(List<Integer> numbers) {
  return numbers.get(0) == 1;
}

O(1) represents a function that always takes the same take regardless of input size.

O(n)

public boolean containsNumber(List<Integer> numbers, int comparisonNumber) {
  for(Integer number : numbers) {
    if(number == comparisonNumber) {
      return true;
    }
  }
  return false;
}

O(n) represents the complexity of a function that increases linearly and in direct proportion to the number of inputs. This is a good example of how Big O Notation describes the worst case scenario as the function could return the true after reading the first element or false after reading all n elements.

O(n²)

public static boolean containsDuplicates(List<String> input) {
  for (int outer = 0; outer < input.size(); outer++) {
    for (int inner = 0; inner < input.size(); inner++) {
      if (outer != inner && input.get(outer).equals(input.get(inner))) {
        return true;
      }
    }
  }
  return false;
}

O(n²) represents a function whose complexity is directly proportional to the square of the input size. Adding more nested iterations through the input will increase the complexity which could then represent O(n³) with 3 total iterations and O(n⁴) with 4 total iterations.

O(2ⁿ)

public int fibonacci(int number) {
  if (number <= 1) {
    return number;
  } else {
    return fibonacci(number - 1) + fibonacci(number - 2);
  }
}

O(2ⁿ) represents a function whose performance doubles for every element in the input. This example is the recursive calculation of Fibonacci numbers. The function falls under O(2ⁿ) as the function recursively calls itself twice for each input number until the number is less than or equal to one.

O(log n)

public boolean containsNumber(List<Integer> numbers, int comparisonNumber) {
  int low = 0;
  int high = numbers.size() - 1;
  while (low <= high) {
    int middle = low + (high - low) / 2;
    if (comparisonNumber < numbers.get(middle)) {
      high = middle - 1;
    } else if (comparisonNumber > numbers.get(middle)) {
      low = middle + 1;
    } else {
      return true;
    }
  }
  return false;
}

O(log n) represents a function whose complexity increases logarithmically as the input size increases. This makes O(log n) functions scale very well so that the handling of larger inputs is much less likely to cause performance problems. The example above uses a binary search to check if the input list contains a certain number. In simple terms, it splits the list in two on each iteration until the number is found or the last element is read. This method has the same functionality as the O(n) example — although the implementation is completely different and more difficult to understand. But, this is rewarded with a much better performance with larger inputs (as seen in the table).

The downside of this sort of implementation is that a Binary Search relies on the elements to already be in the correct order. This adds a bit of overhead performance wise if the elements need to be ordered before traversing through them.

There is much more to cover about Big O Notation but hopefully you now have a basic idea of what Big O Notation means and how that can translate into the code that you write.