Simplifying Logistic Regression

Logistic regression is one of the most popular machine learning algorithms for binary classification. This is because it is a simple algorithm that performs very well on a wide range of problems. It is used when you know that the data is linearly separable/classifiable and the outcome is binary or dichotomous but it can be extended when the dependent has more than two categories. Logistic regression is used when the outcome is a discrete variable, such as trying to figure out who will win the election, whether a student will pass an exam or not, or whether an email is a spam. This is commonly called as a classification problem because we are trying to determine which class the dataset best fits.

Linear Regression vs. Logistic Regression

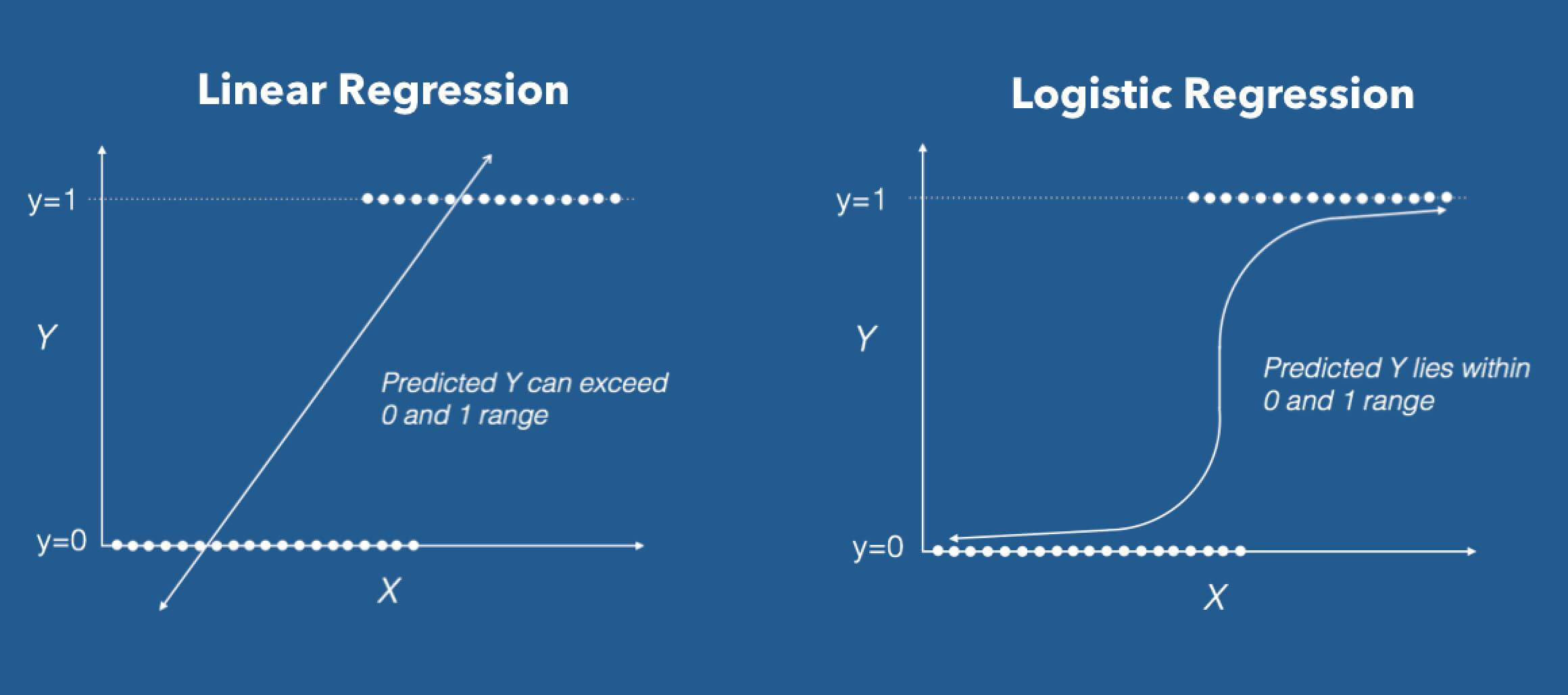
In linear regression, the outcome is continuous. It can have any one of an infinite number of possible values while In logistic regression, the outcome has only a limited number of possible values, generally 0 or 1.

Linear regression needs to establish the linear relationship between dependent and independent variable whereas it is not necessary for logistic regression.

In linear regression, the independent variables can be correlated with each other. On the contrary, in logistic regression, the variable must not be correlated with each other.

Terminology Used for Logistic Regression

• Probability: Probability is the measure of the likelihood that an event will occur.Probability is quantified as a number between 0 and 1.
• Odds: Odds is the ratio of the probability of occurring of an event and probability of not occurring such as odds = P(Occurring)/P(Not occurring) where P = Probability.
• Odds ratio: Odds ratio for a variable in logistic regression that represents how the odds change with 1 unit increase in that variable holding all the other variables as constant. It can be defined as the ratio of two odds.
• Logit: In logistic regression, we need a function that can link independent variables or map the linear combination of variables that could result in any value from 0 to 1. That function is called logit: ln(odds) = ln(p/1-p) = logit(p).

In logistic regression, we estimate an unknown probability for any given linear combination of independent variables.

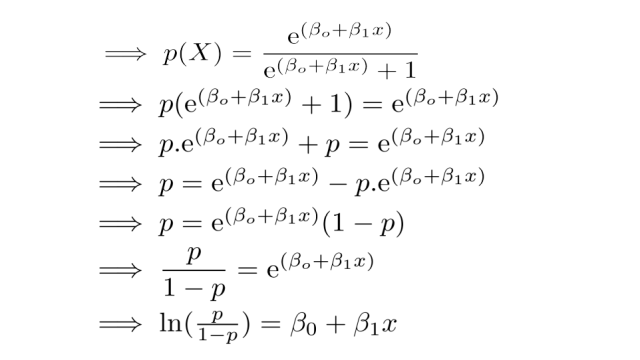
Regression coefficients for logistic regression are calculated using maximum likelihood estimation (MLE).

So, in the above equation, x is the independent variable and the rest of them are regression coefficients. This equation is called estimated regression.

Applications of Logistic Regression

Logistic regression can be applied anywhere that the outcome is binary, such as 0 or 1. Some of the applications of logistic regression are:

1. Predicting whether a student will pass or not on the basis of hours of study or any relevant information.
2. Predicting the approval of loan on the basis of credit score.
3. Predicting the failure of a firm.

This article was first published on the Knoldus blog.