Solving Unique Search Requirements Using TreeMap Data Structure

TreeMap is a Java collection that structures the data in the form of an ordered key and their respective values. It has been available since JDK 1.2. Internally, TreeMap uses a red-black tree to structure the data, which is a self-balancing binary tree. The keys in TreeMap are unique identifiers, and by default, TreeMap arranges the data in a natural ordering of keys. 

For the integer keys, it is stored in the ascending order of the keys, and for the String key, the data will be stored in the alphabetic order. We can always override the default ordering of data and can inject custom sorting by using a comparator during the TreeMap creation to sort in any defined manner as per the logic provided in the comparator. We will discuss in detail a few of the custom hybrid sorting approaches along with some code examples in this article.

One of the most popular searching and sorting data structures is the binary search tree (BST). When it comes to search operation performance, a binary search tree has a worst-case complexity of O(n), which is almost like a linear search. 

Red-black trees have a consistent time complexity of O(log n) as it self-balances itself for every insertion and deletion operation and ensures that the tree is always balanced. This means that the tree adjusts itself automatically in an optimal manner, which ensures the search and find operation is very efficient and never exceeds the O(log n) time complexity for any dataset as well as any kind of search operation. 

It uses a simple but powerful mechanism to maintain a balanced structure by coloring each node in the tree either red or black. It can be called a self-balancing binary search tree. It has good, efficient, worst-case running time complexity.

Why Use TreeMap?

Most of the BST operations (like search, delete, search, and update) take O(log n) time, where n is the number of nodes in the binary search tree. The cost of these operations may become O(n) for a skewed binary tree where all the key is going in one specific path, i.e., it's either a left-skewed binary tree where all elements go on the left path only or a right-skewed binary search tree where all elements go to the right path in the binary search tree. These types of  scenarios with skewed dataset will make the binary search tree highly in-efficient, where all kinds of operations will be very time-consuming.

In addition to the search operation, the insertion or deletion operation will also take O(n) time complexity for the worst-case scenario. This type of situation will result in a totally unbalanced binary search tree, and the height of the tree is almost equal to the number of nodes in the tree. 

If we make sure that the height of the tree remains O(log n) after every insertion and deletion, then we can ensure an upper bound of O(log n) for all these operations, even for the worst-case scenario where the data is highly skewed. This is achieved by introducing the red-black tree, where the tree is always balanced irrespective of the data being skewed or non-skewed. The height of a red-black tree is always O(log n), where n is the number of nodes in the tree.

By default, the red-black tree has the following properties, which are inherently available in the TreeMap dataset.

1. Every node has references to the parent, right child, and left child node in the TreeMap. There can be these three references or reduced references in TreeMap if any node is not present.
2. The left child element key will always have a lesser value compared to the parent element key value.
3. The right child element key will always have a greater than or equal value compared to the parent element key value in TreeMap.
4. Each tree node is colored either red or black.
5. The root node of the tree is always black.
6. Every path from the root to any of the leaf nodes must have the same number of black nodes.
7. No two red nodes can be adjacent; i.e., a red node cannot be the parent or the child of another red node.

If you see the table below, the time complexity is always the same for the red-black tree in any of the data scenarios, and it’s not impacted by the data skewness and always behaves consistently. This makes the TreeMap a very efficient and widely used data structure to deal with high volume data sets where we are not certain about the skewness of the underlying data in the dataset, and we can perform few unique kinds of operations on TreeMap which are not possible in other map data structures like HashMap.

 Time Complexity

Search operation in case of extremely skewed data, which is the worst-case scenario to structure the data in a binary search tree, red-black tree works better for the worst-case scenario. Red-black trees can be used to efficiently index data in databases, allowing for techniques requiring fast search and retrieval of data.

In this article, I am not going to explain the red-black algorithm in detail, but we will focus on a few of the niche functionalities provided by TreeMap, which is one prominent implementation of the red-black tree.

Why Treemap Is Used 

TreeMap Class in Java provides a rich API with various kinds of search operations. It not only provides equal search operation where the element to be searched is present in the map but also other kinds of niche search operations like finding an element in the map which is next higher or next lower compared to the given element. 

Also, the submap of the map with element is the given range. These kinds of complex search operations are only possible if the keys are arranged in an order, and TreeMap is the data structure that is very apt to handle such processing requirements. The search operation usually takes O(log n) time to return the result. Unlike HashMap, which only takes a constant time, it takes a logarithmic time to perform the search operations. This makes one wonder why it was introduced in the first place. 

The answer is even if the search is faster for HashMap for scenarios that don’t fall in the worst-case category for HashMap to provide optimal search with constant time complexity, the data is saved in a memory in a contiguous manner. For TreeMap, there is no such limitation, and it only uses the amount of memory needed to hold/ store the items, unlike HashMap, which uses a contiguous region of memory. Another key reason, as discussed above, is TreeMap provides features to perform niche search operations, which is not always finding the given key in the map but finding other keys, which might be just the next higher, next lower, or the lowest key or a portion of the dataset for a given key range.

Unlike HashMap, which provides only equal search operation where the value to be searched is equal to any key in the Map, TreeMap provides the ability to perform various kinds of search operations structured in the form of TreeMap. This ability to search makes TreeMap a very crucial data structure to solve complex search use cases, and I, in my experience, have used it extensively to solve many complex business requirements. Below are a few of the most prominent search functionalities provided by TreeMap. We will first make ourselves acquainted with the basic features provided by TreeMap and post that will discuss a few niche search requirements where we will bundle multiple features to arrive at a niche requirement for different kinds of search functionalities:

1. floorKey(K key): This function searches for the key in the TreeMap, which is the greatest key less than or equal to the given key. If the function is not able to find any such key, it will return null.
2. ceilingKey(K key): This function searches for the key in the TreeMap, which is the least key greater than or equal to the given key. If the function is not able to find any such key, it will return null.
3. higherKey(K key): This function searches for the key in the TreeMap, which is the least key strictly greater than the given key. If the function is not able to find any such key, it will return null.
4. lowerKey(K key) This function searches for the key in the TreeMap, which is the greatest key strictly less than the given key. If the function is not able to find any such key, it will return null.
5. subMap(K from Key, K toKey): This function searches for the view of the portion of this map whose keys range from fromKey, inclusive, and toKey, exclusive.
6. tailMap(K fromKey): This function searches for the view of the portion of this map whose keys are greater than or equal to fromKey.
7. headMap(K toKey): This function searches for the key-value mapping associated with the least key strictly greater than the given key or null if there is no such key.

Now we have gone through the key features and different kinds of search functionalities provided by a TreeMap, we will try to understand it better with code examples, and later we will try to define some new niche search and data structuring features using different combinations of the above listed TreeMap features:

Use-Case

We will be using the employee entity, which will be captured in the entity class below. This class has a few key employee traits for illustrating the use case.

In the below employee class, in addition to employee identifier attributes, we are capturing a few additional distinct attributes that will be used in the use case. These attributes are as follows:

1. lastYearRating: This holds the last year's appraisal rating for the employee.
2. tenure: This holds the rounded number of years an employee has spent with the organization.
3. currentSalary: This attribute stores the current annual salary of the employee.

class Employee {
     String empName;
     String designation;
     Integer empId;
     String lastYearRating;
     Integer tenure;
     Integer currentSalary;
 
     public Employee(String empName, String designation, Integer empId, String lastYearRating, Integer tenure, Integer currentSalary) {
         this.empName = empName;
         this.designation = designation;
         this.empId = empId;
         this.lastYearRating = lastYearRating;
         this.tenure = tenure;
         this.currentSalary = currentSalary;
     }
 
     @Override
     public String toString() {
         return "Employee{" +
                 "empName='" + empName + '\'' +
                 ", designation='" + designation + '\'' +
                 ", empId=" + empId +
                 ", lastYearRating='" + lastYearRating + '\'' +
                 ", tenure=" + tenure +
                 ", currentSalary=" + currentSalary +
                 '}';
     }
 
     public Integer getCurrentSalary() {
         return currentSalary;
     }
 
     public void setCurrentSalary(Integer currentSalary) {
         this.currentSalary = currentSalary;
     }
 
    public String getEmpName() {
         return empName;
     }
 
     public void setEmpName(String empName) {
         this.empName = empName;
     }
 
     public String getDesignation() {
         return designation;
     }
 
     public void setDesignation(String designation) {
         this.designation = designation;
     }
 
     public Integer getEmpId() {
         return empId;
     }
 
     public void setEmpId(Integer empId) {
         this.empId = empId;
     }
 
     public String getLastYearRating() {
         return lastYearRating;
     }
 
     public void setLastYearRating(String lastYearRating) {
         this.lastYearRating = lastYearRating;
     }
 
     public Integer getTenure() {
         return tenure;
     }
 
     public void setTenure(Integer tenure) {
         this.tenure = tenure;
     }
 
 }

In the below code illustrations, we will use TreeMap features to solve a few niche scenarios:

1. We will bucket all the employees as per the tenure bucket for the organization: We will have six tenure buckets and will place every employee record in the right bucket they belong. This will use a few niche functions provided by TreeMap and will be depicted as being done in a very simplified manner.
2. Next, we will associate the right tenure bucket to every employee.

import java.util.ArrayList;
 import java.util.TreeMap;
 
 public class TreeMapCeilingFloorExample {
     public static void main(String[] args) {
         TreeMap<Integer, Object> tenureTreeMap = new TreeMap<>();
         /* employee List, for illustration purpose just creating few dummy entries but in actual it can be read from source
          * and can run into very high numbers including all employees for the organization */
         ArrayList<Employee> empList = new ArrayList<Employee>();
         empList.add(new Employee("John", "Engineer", 24, "A1", 6,150000));
         empList.add(new Employee("David", "Manager", 35, "A2", 3,145000));
         empList.add(new Employee("Fred", "Architect", 41, "B1", 2, 155000));
         empList.add(new Employee("Brad", "Engineer", 21, "A3", 8,120000));
         empList.add(new Employee("Jason", "Engineer", 32, "A1", 4,170000));
         empList.add(new Employee("Adam", "Senior Engineer", 12, "A1", 14,85000));
         empList.add(new Employee("Christie", "Director", 10, "A1", 15,178000));
         empList.add(new Employee("Martha", "Accountant", 26, "A1", 6,85000));
         empList.add(new Employee("Diana", "Engineer", 28, "A1", 6,108000));
         empList.add(new Employee("Lisa", "Developer", 14, "A1", 12,82000));
          /*  Adding the default buckets for the employee tenures with 0-5, 6- 10, 11-15, 16-20, 21-25, 26-30
          * Adding only higher bound as key so can efficiently use ceiling function to categorize all employees into right bucket */
         tenureTreeMap.put(5, new ArrayList<Employee>());
         tenureTreeMap.put(10, new ArrayList<Employee>());
         tenureTreeMap.put(15, new ArrayList<Employee>());
         tenureTreeMap.put(20, new ArrayList<Employee>());
         tenureTreeMap.put(25, new ArrayList<Employee>());
         tenureTreeMap.put(30, new ArrayList<Employee>());
         /* Using ceilingKey function to check for every employee record and adding the employee to the right bucket.
          * This is a simple illustration leveraging ceilingKey function to easily bucket employees into the right bucket */
         empList.forEach(employeeObj -> {
             Integer key = tenureTreeMap.ceilingKey(employeeObj.getTenure());
             ArrayList matchingList = (ArrayList) tenureTreeMap.get(key);
             matchingList.add(employeeObj);
             tenureTreeMap.put(key, matchingList);
         });
         // Printing all Employees in the bucket starting with lowest to highest
         tenureTreeMap.forEach((key, value) -> {
             System.out.println("Key : " + key + " Value : ");
             ((ArrayList) value).forEach(empObj -> System.out.println());
         });
 
        
     }
 
 }

Result

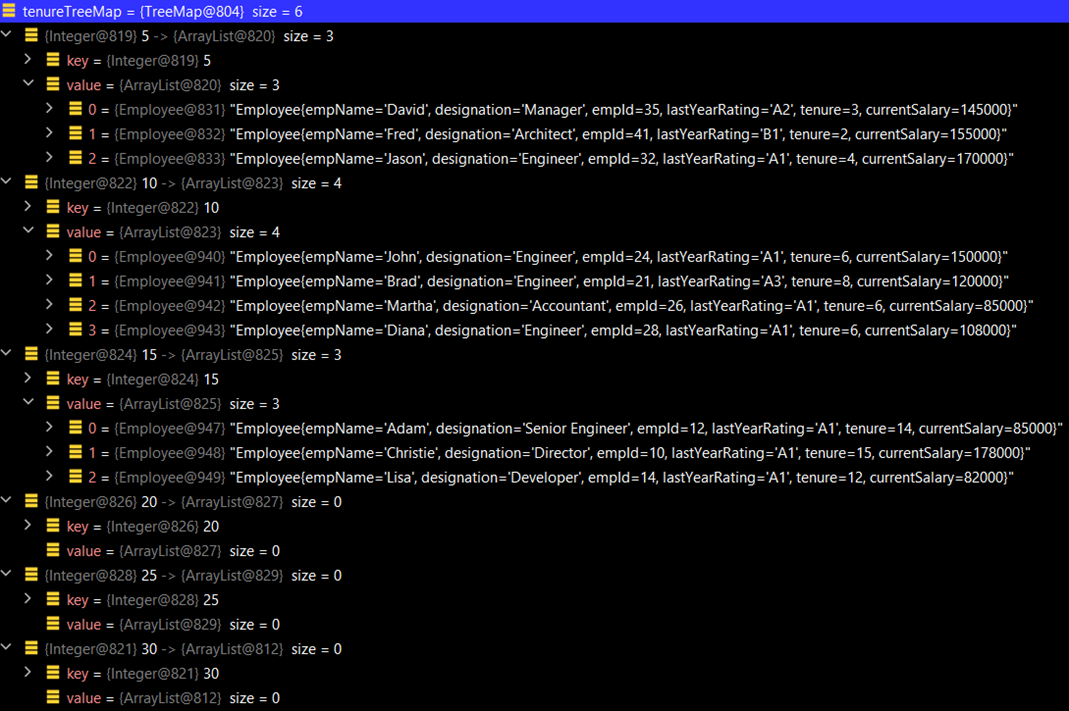
Below is the depiction of the tenure TreeMap, where every employee is bucketed into the right tenure category. The key is the higher bound of the tenure bucket, and lower bound is the higher bound of the prior record+ 1. This is an efficient way to structure the data as per the given range. We are here having six tenure buckets as follows:

• 0 Year to 5 Year: For this range, the key is five, which is the upper bound of this bucket. Three employee records fall into this bucket.
• 6 Year to 10 Year: For this range, the key is ten, which is the upper bound of this bucket. Four employee records fall into this bucket.
• 11 Year to 15 Year: For this range, the key is 15, which is the upper bound of this bucket. Three employee records fall into this bucket.
• 16 Year to 20 Year: For this range, the key is 20, which is the upper bound of this bucket. No employee record falls into this bucket.
• 21 Year to 25 Year: For this range, the key is 25, which is the upper bound of this bucket. No employee record falls into this bucket.
• 26 Year to 30 Year: For this range, the key is 30, which is the upper bound of this bucket. No employee record falls into this bucket.

Remember that the TreeMap uses the natural ordering of the keys (or a custom comparator if provided) to determine the order of elements. Make sure to import the TreeMap class and handle the cases where the methods return null if there's no suitable key according to your use case.

The below code function associates the tenure range for every employee record. The result is also printed beneath the code, showing the tenure range for every employee record. The TreeMap is created with the key as the upper bound of the tenure range, and all the employees for the given tenure range are in the value corresponding to the given key in the form of an array list. 

The below-listed code uses ceiling and floor functions to find the lower bound and upper bound for any key in the TreeMap. In the below scenario, we are trying to find out the tenure range for every employee record by getting the lower bound using the lowerKey function. Next upper bound is determined using ceilingEntry method, and the range string is formed and associated with every employee record. This is a simple illustration to show the power of TreeMap functionality to easily accomplish complex requirements by leveraging the in-built functions.

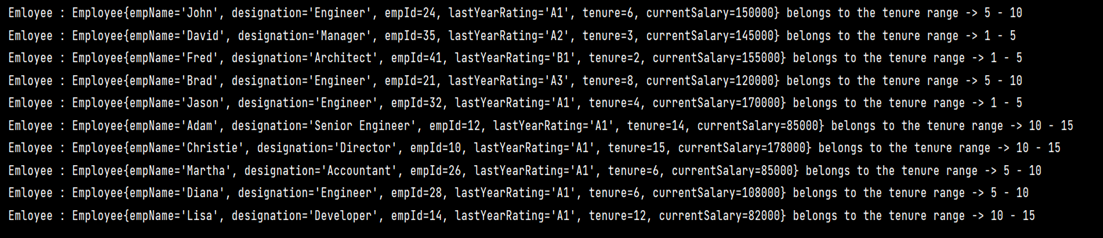
Result: In the below output, every employee has an associated tenure bucket associated with the record.

Hope this article helped you to get acquainted with TreeMap data structure and helped with some scenarios to use the in-built TreeMap functions to solve complex data categorization and search requirements.

I solved a few scenarios for the tenure use cases to bucket the data efficiently and use the bucketed data to perform complex search operations using TreeMap and a combination of in-built functions from TreeMap. I have added lastYearRating as well currentSalary attributes in the employee class. As a next step to gain some more hands-on experience working with TreeMap, please try to solve bucketing the data as per different salary buckets using TreeMap in-built functions and try to play around with different kinds of search operations on the TreeMap data bucketed as per salary range. Do let me know if you have any questions or need any further clarification on the topics discussed in this article.