Understanding AVL Trees in C#: A Guide to Self-Balancing Binary Search Trees

In my previous article, we discussed the binary search tree and its implementation in C#. We learned that this data structure allows for fast searching, insertion, and deletion of elements in logarithmic time. Still, if the tree is not balanced properly, its performance can suffer greatly. We also noted that there is a more advanced tree called AVL with self-balancing, which guarantees logarithmic time complexity for all operations, regardless of the incoming data.

In this article, we will continue our exploration of binary search trees by diving deeper into AVL Trees. We will discuss their structure, properties, and implementation details and compare them to other self-balancing trees. We will also provide examples of AVL Trees in action and demonstrate how they solve the problem of unbalanced trees. By the end of this article, you will have a solid understanding of AVL Trees and be equipped with the knowledge to use them effectively in your own code.

This article is a direct continuation of my previous article Unlocking the Potential of Binary Search Trees with C# Programming, in which I covered the implementation of the basic methods of Binary Search Trees, such as adding and removing elements. Therefore, to better understand the code with me, I recommend that you first read my previous article.

The entire concept of a binary tree remains the same. The only thing that will be added is the balancing of the tree during the insertion of a new node or the removal of an old one. Our task is to ensure that the difference between the heights for each child node always remains less than or equal to one in absolute value.

It may look complicated, but in reality, the height of an individual node is just the longest path from its child to the lowest leaf. Therefore, a node without children will have a height of 0. And a non-existent node will have a height of -1.

Updating Node Heights When Adding Values

It is obvious that when adding and removing nodes, the height of the parents in the recursive chain will change. This means that during stack unwinding, we need to update the height for each node in the stack. This is why the recursive algorithm is extremely convenient here.

We will update the height for each such node as follows. We will take the height of the left and right child. Then we will keep the larger of the two and add one to it. Thus, the height of the nodes will either increase by one or decrease by one.

It should be understood that during insertion, the height will only change when a new node is added to a leaf. Because if a node already has one child and another child is added to it, the height will not change as a result.

private class Node
{
    ...

    private int _height;

    ...
    
    public void Insert(T value)
    {
        ref var branch = ref value.CompareTo(Value) < 0 
            ? ref _left 
            : ref _right;

        if (branch is null)
        {
            branch = new Node(value);
        }
        else
        {
            branch.Insert(value);
        }
        
        UpdateHeight();
    }

    ...
    
    private void UpdateHeight()
    {
        var maxHeight = Math.Max(
            _left?._height ?? -1,
            _right?._height ?? -1);
        
        _height = maxHeight + 1;
    }
}

Left and Right Rotations

After adding new elements to the tree and recalculating the height for the nodes in the stack, we need to determine whether our tree remains balanced or not.

In other words, this is called tree overload. It can be overloaded either to the left or to the right side.

Overload is defined as the situation where the difference between the heights of the right and left subtrees for a given node is greater than 1 in absolute value. This will be the signal for balancing. But the sign will show us in which direction the tree is overloaded. If we get a negative value, it means the height is greater on the left, so we balance to the right. If we get a positive difference, it means the height is greater on the right, so we balance to the left.

Balancing means that we have to rotate our tree either to the left or to the right while preserving the order of the nodes.

In essence, a right rotation simply means that if, in the beginning, the node around which we rotate the tree pointed to its left child, now the left child will point to its parent from the right side and vice versa.

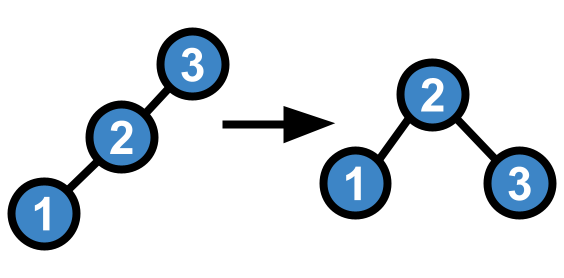
It is important to remember that there may be a parent node referencing this node from above. Therefore, the links must be carefully changed so as not to disrupt anything.

In addition, these two nodes may also have children. To handle this, we will create an auxiliary method that simply swaps the keys and values for these two nodes.

private class Node
{
    ...
    
    private static void Swap(Node a, Node b)
    {
        (a.Value, b.Value) = (b.Value, a.Value);
    }
}

The last thing to do is to update the heights of these two nodes, which will change after the rotation. First, the lower node, then the upper one. The same logic applies to a left rotation; only all actions will be completely mirrored.

private class Node
{
    ...
    
    private void RotateToRight()
    {
        if (_left is null)
        {
            throw new InvalidOperationException(
                "Could not rotate to the right.");
        }
        
        Swap(this, _left);
        var formerRight = _right;
        _right = _left;
        _left = _right._left;
        _right._left = _right._right;
        _right._right = formerRight;
        _right.UpdateHeight();
        UpdateHeight();
    }
    
    private void RotateToLeft()
    {
        if (_right is null)
        {
            throw new InvalidOperationException(
                "Could not rotate to the left.");
        }
        
        Swap(this, _right);
        var formerLeft = _left;
        _left = _right;
        _right = _left._right;
        _left._right = _left._left;
        _left._left = formerLeft;
        _left.UpdateHeight();
        UpdateHeight();
    }
}

Right-Left and Left-Right Rotations

An AVL tree can have not only left and right rotations but also Right-Left and Left-Right rotations. If we have a tree like this.

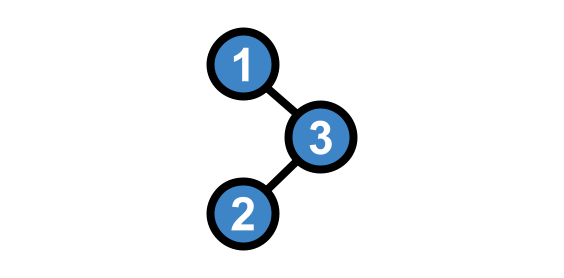
We will also need a right-left rotation in such a situation. In this case, we first need to rotate the tree to the right with respect to the middle node, which will bring us to the previous situation that we just discussed and already know how to work with. Therefore, we now rotate the resulting tree to the left with respect to the upper node and again come to balance.

The same applies to the left-right rotation, which is just a mirror image of the previous one. To determine when to perform a simple right rotation or a left-right rotation, we need to check the balance of the children. If the tree is overloaded to the left, we check the balance of the left child. If the tree takes a crooked form, then we will get the number 1. Therefore, we immediately perform a left rotation with respect to node one and only then perform a right rotation.

If our tree had a straight shape, the balance of node 1 would be minus one. Therefore, we would only need one right rotation.

The same logic works for an overloaded tree to the right. Here we check the balance of the right child, and if it is equal to minus one, it means that the tree has a zigzag shape. Therefore, it needs to be rotated to the right first and then to the left.

private class Node
{
    ...

    public void Insert(T value)
    {
        ...
        
        UpdateHeight();
        Balance();
    }

    ...
    
    private int GetOverload()
    {
        return (_right?._height ?? -1) - (_left?._height ?? -1);
    }
    
    private void Balance()
    {
        var overload = GetOverload();

        if (overload == -2)
        {
            if (_left?.GetOverload() == 1)
            {
                _left.RotateToLeft();
            }

            RotateToRight();
        }
        else if (overload == 2)
        {
            if (_right?.GetOverload() == -1)
            {
                _right.RotateToRight();
            }
            
            RotateToLeft();
        }
    }
}

Deletion in AVL Tree

Deletion in AVL trees works exactly the same way as in a binary search tree. The only difference is that, after each deletion, as we unwind the stack during rotation, we will update the height of nodes and balance them if necessary. This will be done not only for the node being deleted but also for the node that replaces the deleted node in the case of two children. Because its deletion may again change the heights of parent nodes. Therefore, we need to recursively traverse each such node up to the deleted node, updating all heights.

private class Node
{
    ...

    public bool Remove(T value, out Node? root)
    {
        bool hasRemoved;
        var comparison = value.CompareTo(Value);

        if (comparison < 0)
        {
            root = this;
            hasRemoved = _left?.Remove(value, out _left) ?? false;
        } 
        else if (comparison > 0)
        {
            root = this;
            hasRemoved = _right?.Remove(value, out _right) ?? false;
        }
        else if (_left is null || _right is null)
        {
            root = _left ?? _right;
            hasRemoved = true;
        }
        else
        {
            var leftMax = _left.Max();
            _left.Remove(leftMax.Value, out _left);
            Value = leftMax.Value;
            root = this;
            hasRemoved = true;
        }

        root?.UpdateHeight();
        root?.Balance();
        return hasRemoved;
    }

    ...
}

Conclusion

So, we have successfully reduced the complexity of our tree to logarithmic time, but the recursion, constant updates of node heights along the recursion path, calculations of balance factors along the recursion path, and execution of multiple rotations along the recursion path significantly slow down the entire algorithm, especially with large amounts of data.

In an attempt to overcome these limitations, another tree was created, which is called a red-black tree. The name comes from the fact that every node in the tree now has a color, which is either red or black.

But I will discuss this type of tree in my next and final article in this series about search trees Red-Black Trees in C#: A Guide to Efficient Self-Balancing Binary Search Trees.