Understanding the CAP Theorem
In this article, we take an exploratory look at one of the more important ideas in the field of data engineering, and where it stands today.
Join the DZone community and get the full member experience.
Join For FreeThe CAP theorem is a tool used to make system designers aware of the trade-offs while designing networked shared-data systems. CAP has influenced the design of many distributed data systems. It made designers aware of a wide range of trade-offs to consider while designing distributed data systems. Over the years, the CAP theorem has been a widely misunderstood tool used to categorize databases. There is much misinformation floating around about CAP. Most blog posts on CAP are historical and possibly incorrect.
It is important to understand CAP so that you can identify the misinformation around it.
The CAP theorem applies to distributed systems that store state. Eric Brewer, at the 2000 Symposium on Principles of Distributed Computing (PODC), conjectured that in any networked shared-data system there is a fundamental trade-off between consistency, availability, and partition tolerance. In 2002, Seth Gilbert and Nancy Lynch of MIT published a formal proof of Brewer's conjecture. The theorem states that networked shared-data systems can only guarantee/strongly support two of the following three properties:
- Consistency — a guarantee that every node in a distributed cluster returns the same, most recent, successful write. Consistency refers to every client having the same view of the data. There are various types of consistency models. Consistency in CAP (used to prove the theorem) refers to linearizability or sequential consistency, a very strong form of consistency.
- Availability — every non-failing node returns a response for all read and write requests in a reasonable amount of time. The key word here is every. To be available, every node on (either side of a network partition) must be able to respond in a reasonable amount of time.
- Partition Tolerant — the system continues to function and upholds its consistency guarantees in spite of network partitions. Network partitions are a fact of life. Distributed systems guaranteeing partition tolerance can gracefully recover from partitions once the partition heals.
The C and A in ACID represent different concepts than C and A in the CAP theorem.
The cap theorem categorizes systems into three categories:
- CP (Consistent and Partition Tolerant) — At first glance, the CP category is confusing, i.e., a system that is consistent and partition tolerant but never available. CP refers to a category of systems where availability is sacrificed only in the case of a network partition.
- CA (Consistent and Available) — CA systems are consistent and available systems in the absence of any network partition. Often a single node's DB servers are categorized as CA systems. Single-node DB servers do not need to deal with partition tolerance and are thus considered CA systems. The only hole in this theory is that single-node DB systems are not a network of shared data systems and thus do not fall under the purview of CAP.
- AP (Available and Partition Tolerant) — These are systems that are available and partition tolerant but cannot guarantee consistency.
A Venn diagram or a triangle is frequently used to visualize the cap theorem. Systems fall into the three categories that are depicted using the intersecting circles. 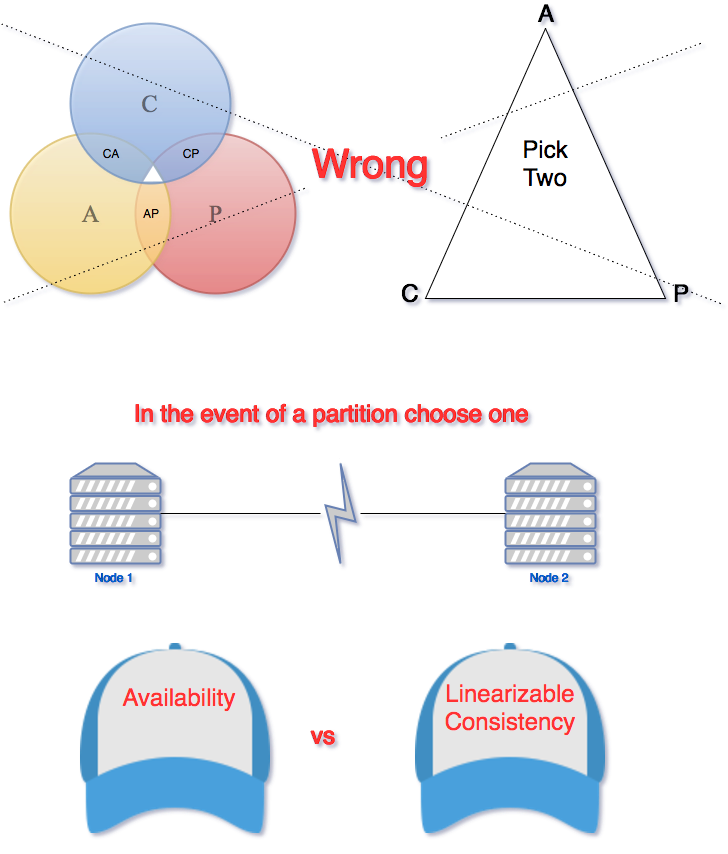
The part where all three sections intersect is white because it is impossible to have all three properties in networked shared-data systems. A Venn diagram or a triangle is an incorrect visualization of the CAP. Any CAP theorem visualization such as a triangle or a Venn diagram is misleading. The correct way to think about CAP is that in case of a network partition (a rare occurrence), one needs to choose between availability and consistency.
In any networked shared-data system, partition tolerance is a must. Network partitions and dropped messages are a fact of life and must be handled appropriately. Consequently, system designers must choose between consistency and availability. Simplistically speaking, a network partition forces designers to either choose perfect consistency or perfect availability. Picking consistency means not being able to answer a client's query as the system cannot guarantee to return the most recent write. This sacrifices availability.
Network partition forces non-failing nodes to reject clients' requests as these nodes cannot guarantee consistent data. At the opposite end of the spectrum, being available means being able to respond to a client's request, but the system cannot guarantee consistency, i.e., the most recent value written. Available systems provide the best possible answer under the given circumstance.
During normal operation (lack of network partition), the CAP theorem does not impose constraints on availability or consistency.
The CAP theorem is responsible for instigating the discussion about the various trade-offs in a distributed shared-data system. It has played a pivotal role in increasing our understanding of shared-data systems. Nonetheless, the CAP theorem is criticized for being too simplistic and often misleading. Over a decade after the release of the CAP theorem, Brewer acknowledges that the CAP theorem oversimplified the choices available in the event of a network partition.
According to Brewer, the CAP theorem prohibits only a “tiny part of the design space: perfect availability and consistency in the presence of partitions, which are rare." System designers have a broad range of options for dealing and recovering from network partitions. The goal of every system must be to “maximize combinations of consistency and availability that make sense for the specific application.”
References
Published at DZone with permission of Akhil Mehra. See the original article here.
Opinions expressed by DZone contributors are their own.

Comments