Visualizing Matrix Multiplication as a Linear Combination
Join the DZone community and get the full member experience.
Join For Freewhen multiplying two matrices, there's a manual procedure we all know how to go through. each result cell is computed separately as the dot-product of a row in the first matrix with a column in the second matrix. while it's the easiest way to compute the result manually, it may obscure a very interesting property of the operation: multiplying a by b is the linear combination of a's columns using coefficients from b . another way to look at it is that it's a linear combination of the rows of b using coefficients from a .
in this quick post i want to show a colorful visualization that will make this easier to grasp.
right-multiplication: combination of columns
let's begin by looking at the right-multiplication of matrix x by a column vector:
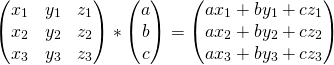
representing the columns of x by colorful boxes will help visualize this:
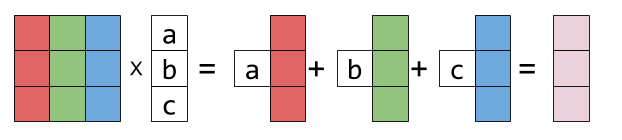
sticking the white box with a in it to a vector just means: multiply this vector by the scalar a. the result is another column vector - a linear combination of x's columns, with a, b, c as the coefficients.
right-multiplying x by a matrix is more of the same. each resulting column is a different linear combination of x's columns:
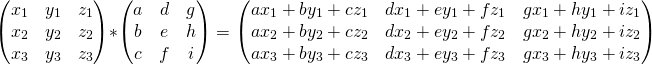
graphically:
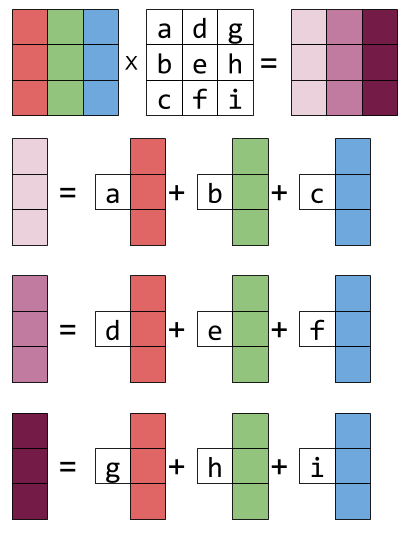
if you look hard at the equation above and squint a bit, you can recognize this column-combination property by examining each column of the result matrix.
left-multiplication: combination of rows
now let's examine left-multiplication. left-multiplying a matrix x by a row vector is a linear combination of x's rows :

is represented graphically thus:
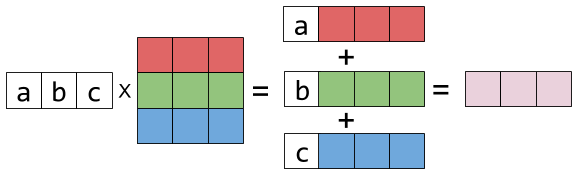
and left-multiplying by a matrix is the same thing repeated for every result row: it becomes the linear combination of the rows of x, with the coefficients taken from the rows of the matrix on the left. here's the equation form:
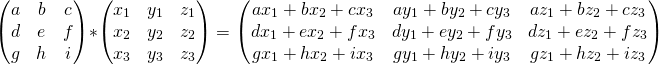
and the graphical form:

Published at DZone with permission of Eli Bendersky. See the original article here.
Opinions expressed by DZone contributors are their own.

Comments