Monte Carlo Estimate for Pi with NumPy

In this post we will use a Monte Carlo method to approximate pi. The idea behind the method that we are going to see is the following:

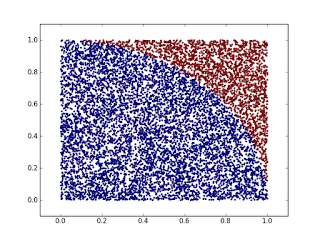
Draw the unit square and the unit circle. Consider only the part of the circle inside the square and pick uniformly a large number of points at random over the square. Now, the unit circle has pi/4 the area of the square. So, it should be apparent that of the total number of points that hit within the square, the number of points that hit the circle quadrant is proportional to the area of that part. This gives a way to approximate pi/4 as the ratio between the number of points inside circle and the total number of points and multiplying it by 4 we have pi.

Let's see the python script that implements the method discussed above using the numpy's indexing facilities:

from pylab import plot,show,axis
from numpy import random,sqrt,pi

# scattering n points over the unit square
n = 1000000
p = random.rand(n,2)

# counting the points inside the unit circle
idx = sqrt(p[:,0]**2+p[:,1]**2) < 1

plot(p[idx,0],p[idx,1],'b.') # point inside
plot(p[idx==False,0],p[idx==False,1],'r.') # point outside
axis([-0.1,1.1,-0.1,1.1]) 
show()

# estimation of pi
print '%0.16f' % (sum(idx).astype('double')/n*4),'result'
print '%0.16f' % pi,'real pi'

The program will print the pi approximation on the standard out:

3.1457199999999998 result
3.1415926535897931 real pi

Note that the lines of code used to estimate pi are just 3!

Source: http://glowingpython.blogspot.com/2012/01/monte-carlo-estimate-for-pi-with-numpy.html